BIOCHEMISTRY TOPICS
Dihedraalhoeken (of torsiehoeken)
Definities van bindingshoek en dihedraalhoek (torsiehoek). Differente hoeken van de hoofdketen van polypeptiden, φ, ψ, en ω. Ramachandran-plots.
De conformatie die biologische moleculen aannemen bepaalt de fysische en chemische eigenschappen die ze in biologische systemen vertonen. Daarom hebben we een manier nodig om de conformatie te beschrijven die wordt waargenomen voor de soorten moleculen die in de biochemie worden bestudeerd. In dit hoofdstuk zal de aandacht vooral uitgaan naar de conformatie van polypeptiden, als voorbereiding op het begrijpen van de structuur-functierelaties in eiwitten
Een tweevlakshoek – ook wel torsiehoek genoemd – wordt gedefinieerd door vier achtereenvolgens aan elkaar gebonden atomen. Dit wordt in de figuur hieronder weergegeven door de structuur A-B-C-D (tweede paneel; let op het onderscheid tussen bindingshoek en torsiehoek). Stel je voor dat je langs de binding tussen de atomen B en C kijkt (zoals aangegeven door de pijl). Dit is de centrale binding van de drie gedefinieerde bindingen. In eerste instantie zien we de binding B-C in het vlak van de figuur, met de binding B-A naar links en omhoog buiten het vlak, en de binding C-D naar beneden en naar rechts. Dan nemen we deze structuur en beginnen hem te draaien, zodat we recht naar beneden kunnen kijken naar de binding B-C (derde paneel). Uiteindelijk is ons beeld gelijk aan de Newman projectie in het laatste paneel. Vanuit dit gezichtspunt is de dihedraalhoek τ de schijnbare hoek die D maakt ten opzichte van A, zoals te zien is. We definiëren het bereik van de waarden van de tweevlakshoeken als , en de waarde van τ is ongeveer -150° (Het negatieve deel van het bereik komt overeen met wanneer D tegen de wijzers van de klok in staat ten opzichte van A.)
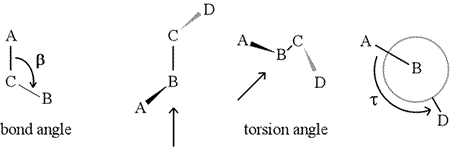
Natuurlijk kunnen er andere atomen aan B en C vastzitten – en meestal is dat ook zo. We zouden moeten specificeren welke atomen corresponderen met A, B, C, en D om ondubbelzinnig de dihedrale hoek te definiëren. Voor lange onvertakte polymeren, zoals eiwitten, is het logisch om te eisen dat A t/m D alle atomen van de hoofdketen zijn. Hieronder staat een molecuulgrafische afbeelding die overeenkomt met bovenstaande schets en die de definitie van de tweevlakshoek Phi (φ) van de hoofdketen van een polypeptide illustreert.
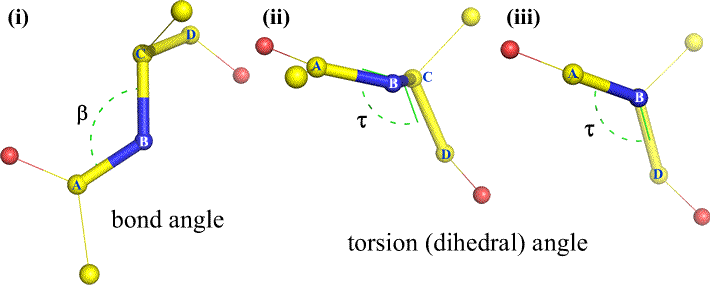
Polypeptide dihedraalhoeken van de hoofdketen: Phi (φ), Psi (ψ), en Omega (ω)
Een dihedrale hoek wordt gedefinieerd door vier atomen. Hij kan worden gevisualiseerd door langs de centrale binding te kijken (d.w.z. de binding van atoom 2 aan atoom 3). De tweevlakshoeken in een polypeptideketen zijn van drieërlei aard:
Phi (φ) – centrale binding tussen N(i) en C(alpha, i) . Kijk naar beneden naar de N(i)-Cα(i) binding, let op de hoek die de acyl-koolstof C(i) maakt ten opzichte van C(i-1) – de acyl-koolstof van het vorige residu.
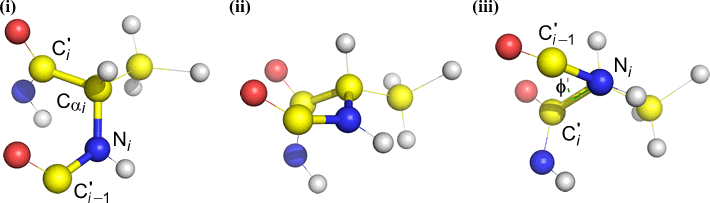
Psi (ψ) – centrale binding tussen C(alpha, i) en C(i) . Kijk naar beneden naar de binding Cα(i)-C(i), let op de hoek die N(i + 1) maakt ten opzichte van N(i).
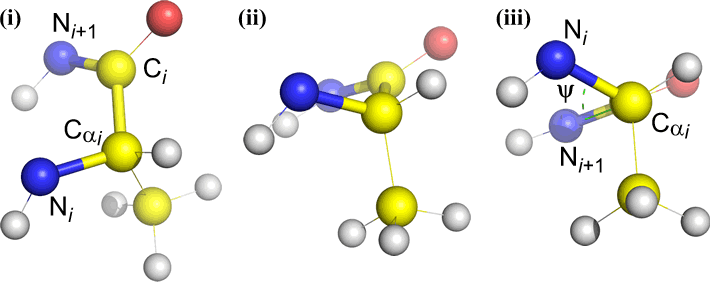
Omega (ω) – de peptidebinding tussen de acyl-koolstof C(i) en N(i+1) is de centrale binding.
Phi (φ) en psi (ψ) worden soms Ramachandran-hoeken genoemd, omdat ze worden gebruikt in een tweedimensionale plot van de dihedraalhoeken van de hoofdketen die een Ramachandran-plot wordt genoemd (zie hieronder).
Ramachandran-plot
De Ramachandran-plot is een grafiek van de dihedraalhoeken phi (φ) en psi (ψ) van de hoofdketen voor een polypeptideketen, met phi (φ)-waarden langs de x-as en psi (ψ)-waarden langs de y-as.
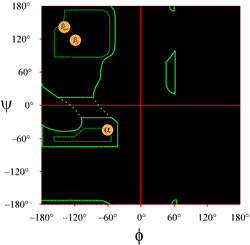
De indeling van een Ramachandran-plot zoals die gewoonlijk in leerboeken wordt gepresenteerd, staat links (klik op de figuur om een grotere versie te zien). De contouren geven de omvang van de toegestane (lichtgroen) en meest favoriete (donkergroen) combinaties van (φ, ψ) aan. De oranje cirkels tonen de locaties van de ideale phi, psi waarden voor de meest voorkomende regelmatige secundaire structuurkenmerken, beta-strengen (in antiparallelle en parallelle vellen) en alpha-helixen. Buiten de contouren zijn de overeenkomstige conformaties niet gewenst of niet toegestaan. De exacte locaties van de contouren moeten niet al te letterlijk worden genomen, omdat de gunstige en toegestane gebieden afhangen van de identiteit van het residu. Glycine, in het bijzonder, heeft veel grotere toegestane gebieden dan hier getoond. Dit wordt hieronder verder besproken.
Een “echte” Ramachandran plot
In het “eindspel” van de proteïnestructuurbepaling moet het experimenteel bepaalde model worden geanalyseerd op zijn stereochemische kwaliteit. Ernstige problemen met het model kunnen worden aangegeven als er gevallen zijn van niet-Gly residuen waarvan de dihedraalhoeken van de hoofdketen buiten de toegestane gebieden liggen, of als een te groot deel van de residuen buiten het meest-voorkeursgebied ligt. Een voorbeeld van een Ramachandran-plot voor een eiwit van 190 residuen is te zien in de bijgaande figuur.
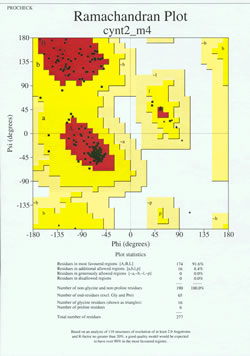
De figuur toont een Ramachandran-plot voor een eiwitstructuur bepaald door röntgen-kristallografie. (Klik erop om een grotere versie te zien in een nieuw venster.) Elk zwart vierkant stelt de conformatie voor van de hoofdketen op één residu van het eiwit. Merk op hoe de phi, psi waarden voor de residuen clusteren in de rode “meest begunstigde” regio’s. Het rode gebied linksboven (in de figuur aangeduid met “B”) komt overeen met residuen in een bètastrengconformatie van de hoofdketen, terwijl het grote gebied in het midden (aangeduid met “A”) overeenkomt met een alfa-helix. Het derde, kleine rode gebied van de plot is waar zich residuen bevinden die een linkshandige (“L”) alfa-helix aannemen. Sommige van de residuen liggen in “extra toegestane gebieden” (helder geel) die grenzen aan de meest begunstigde gebieden. Merk op hoe de glycineresiduen (aangegeven als driehoeken) in sommige gevallen in “niet-toegestane regio’s” liggen. Dit komt omdat glycine, met alleen het kleine waterstofatoom als zijn “zijketen”, veel minder sterisch bezwaard is dan andere aminozuren. Gly is in staat om paren van phi, psi hoeken aan te nemen die voor geen enkel ander residu zijn toegestaan.