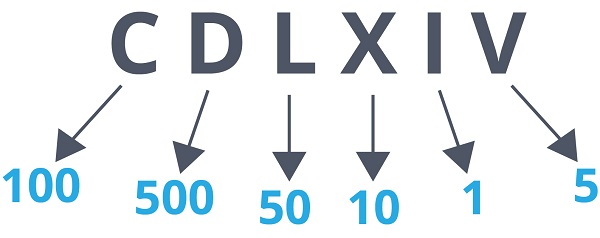Vores selvstyrende K6-læringsplatform er bygget med børn i tankerne, men forældre og lærere elsker den også.

Lær om romertal

Se på dette ur. Det bruger nogle symboler til at vise tallene 1-12.

Ved du, hvad disse tal hedder?

Tal som I, VI og IX kaldes romerske tal (eller romerske tal).

Disse tal blev opfundet af de gamle romere for næsten 3.000 år siden! De brugte symboler til at skrive tal.

I denne lektion skal vi lære, hvordan man læser og skriver romertal.

Romertal 1 – 10

Sådan tæller du fra 1 til 3 med romertal:

I = 1

II = 2

III = 3

Nemt indtil videre, ikke sandt?

Kan du gætte, hvad 4 er? Du tror måske, at det er 4 I’er, men det er faktisk:

IV = 4

Hvad er det for et V-symbol?

I romertal er V symbolet for 5.

V = 5

I romertal skriver man aldrig mere end 3 af det samme symbol i en række.

Der er derfor, at efter III kommer IV.

Så hvad tror du, der kommer efter V?

Vi tilføjer endnu et I.

VI = 6

Vi kan tilføje endnu et I for at få 7.

VII = 7

I romerske tal er det i orden at have 3 af et symbol i en række, men ikke flere. Så efter 7 kommer:

VIII = 8

Hvad skal vi nu gøre? Vi kan ikke tilføje endnu et I. Så vi skal bruge et nyt større symbol:

X = 10

For at lave 9 tager vi 1 fra 10:

IX = 9

Husk: Når vi skriver I foran et større symbol som V eller X, tager vi 1 fra det pågældende tal.

Godt gået med at lære at tælle fra I til X i romertal!

For at tælle til 10 har du været nødt til at bruge 3 af de symboler, der udgør romertal: I, V, X.

Nu skal du lære de 4 andre symboler: L, C, D og M.

Romertal L, C, D, M

Romerske tal består alle af syv symboler.

Du har lært I, V og X. Her er de 4 større symboler:

L = 50

C = 100

Tip: Et århundrede er 100 år. Det begynder med c.

D = 500

M = 1.000

Tip: et årtusinde er 1.000 år! Det starter med m.

TIP!

Du kan bruge denne sætning som hjælp til at huske rækkefølgen:

Regler for romertal

Alle romertal er kombinationer af de 7 grundsymboler.

Disse kombinationer følger fire vigtige regler:

Regel 1: Når et mindre symbol kommer efter et større symbol, lægges det til.

Til eksempel,

VI = 5 + 1 = 6

Regel 2: Hvis et symbol kommer efter sig selv, lægges det til.

XX = 10 + 10 = 20

CCLX = 100 + 100 + 50 + 10 = 260

Regel 3: Hvis et mindre symbol kommer før et større symbol, trækkes det fra.

For eksempel,

IX = 10 – 1 = 9

XL = 50 – 10 = 40

CM = 1000 – 100 = 900

Regel 4: Det samme symbol kan ikke bruges mere end tre gange i træk.

For eksempel,

XXX = 10 + 10 + 10 + 10 = 30, men 40 er ikke XXXX.

CCC = 100 + 100 + 100 + 100 = 300, men 400 er ikke CCCC.

Romertal – grundtal

Lad os nu bruge disse regler til at lære nogle grundtal i romertal.

1 = I

2 = 1 + 1 = II

3 = 1 + 1 + 1 + 1 = III

4 = 5 – 1 = IV

5 = V

6 = 5 + 1 = VI

7 = 5 + 1 + 1 + 1 = VII

8 = 5 + 1 + 1 + 1 + 1 = VIII

9 = 10 – 1 = IX

10 = X

20 = 10 + 10 = XX

30 = 10 + 10 + 10 + 10 = XXX

40 = 50 – 10 = XL

50 = L

60 = 50 + 10 = LX

70 = 50 + 10 + 10 + 10 = LXX

80 = 50 + 10 + 10 = LXXX

90 = 100 – 10 = XC

100 = C

200 = 100 + 100 = CC

300 = 100 + 100 + 100 + 100 = CCC

400 = 500 – 100 = CD

500 = D

600 = 500 + 100 = DC

700 = 500 + 100 + 100 + 100 = DCC

800 = 500 + 100 + 100 + 100 = DCCC

900 = 1000 – 100 = CM

1000 = M

Godt arbejde!

CDLXIV

Nu skal vi lære at læse og skrive andre romertal.

Konvertering af romertal til cifre

Se på dette romertal.

CDLXIV

Hvordan vil du konvertere det til cifre? Det er rigtigt!

For at omdanne et romertal til cifre skal du finde værdien af hvert symbol i det og derefter addere eller trække disse værdier fra hinanden.

Lad os prøve at gøre det nu!

Lad os først finde værdien af hvert symbol.

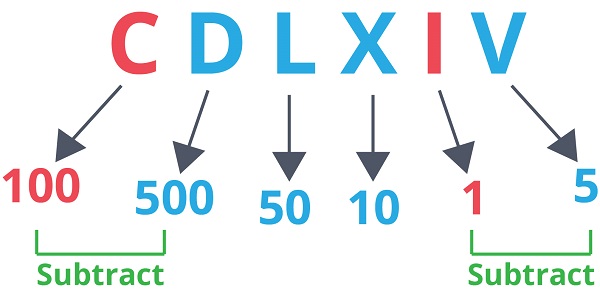
Lad os nu se, om der er mindre symboler, der optræder før større symboler.

Det er fordi, vi skal trække disse værdier fra (regel 3)!

Her er regel 3 en gang til:

Regel 3: Når et mindre symbol optræder før et større symbol, trækkes det fra.

Lad os nu addere/subtrahere værdierne.

CDLXIV = (500 – 100) + (50 + 10) + (5 – 1)

= 400 + 60 + 4

Så hvad er værdien af dette romertal?

Korrekt!

CDLXIV = 464

Fantastisk!

Lad os prøve endnu et eksempel.

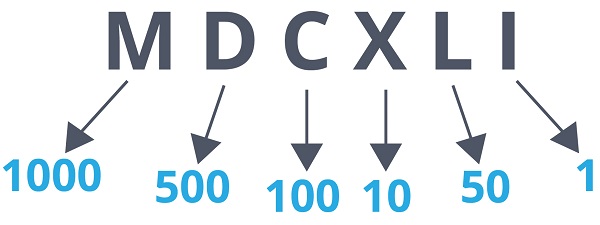
Konverter dette romertal til cifre.

MDCXLI

Lad os gøre det!

Hvordan skal vi begynde?

Først finder vi værdierne for alle symbolerne.

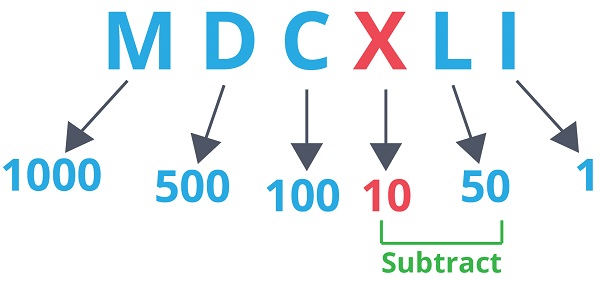
Dernæst finder vi eventuelle mindre symboler, der optræder før større symboler.

Lad os nu lægge værdierne sammen/trække dem fra hinanden.

MDCXLI = 1000 + (500 + 100) + (50 – 10) + 1

= 1000 + 600 + 40 + 1

Så værdien af dette romertal er:

MDCXLI = 1.641

Perfekt!

Konvertering af cifre til romertal

Lad os nu prøve at konvertere dette tal til et romertal.

2,342

Hvordan vil du gøre det?

Meget godt!

For at omdanne et tal til et romertal skal du opdele tallet i værdierne I, V, X, L, C, D, M.

Lad os prøve!