BIOCHEMIE-THEMEN
Flächen- (oder Torsions-) winkel
Definitionen von Bindungswinkel und Dihdral- (Torsions-) winkel. Polypeptid-Hauptketten-Dihedralwinkel, φ, ψ und ω. Ramachandran-Diagramme.
Die Konformationen, die biologische Moleküle annehmen, bestimmen die physikalischen und chemischen Eigenschaften, die sie in biologischen Systemen aufweisen. Daher benötigen wir eine Möglichkeit, die Konformationen zu beschreiben, die für die in der Biochemie untersuchten Molekülarten beobachtet werden. Das Hauptaugenmerk in diesem Abschnitt liegt auf den Konformationen von Polypeptiden als Vorbereitung für das Verständnis der Struktur-Funktions-Beziehungen in Proteinen
Ein Flächenwinkel – auch Torsionswinkel genannt – wird durch vier aufeinanderfolgend gebundene Atome definiert. Dies wird in der Abbildung unten durch die Struktur A-B-C-D dargestellt (zweite Tafel; beachten Sie den Unterschied zwischen Bindungswinkel und Torsionswinkel). Stellen Sie sich vor, Sie schauen entlang der Bindung zwischen den Atomen B und C (wie durch den Pfeil angezeigt). Dies ist die zentrale Bindung der drei definierten Bindungen. Zunächst sehen wir die B-C-Bindung in der Ebene der Abbildung, wobei die B-A-Bindung nach links und nach oben aus der Ebene heraus zeigt und die C-D-Bindung nach unten und nach rechts. Dann nehmen wir diese Struktur auf und beginnen sie so zu drehen, dass wir gerade auf die B-C-Bindung hinunterschauen können (dritte Tafel). Schließlich entspricht unsere Ansicht der Newman-Projektion im letzten Feld. Aus dieser Sicht ist der Dihedralwinkel τ der scheinbare Winkel, den D relativ zu A einnimmt, wie gezeigt. Wir definieren den Wertebereich des Flächenwinkels als , und der Wert von τ liegt bei etwa -150° (der negative Teil des Bereichs entspricht dem Fall, dass D gegen den Uhrzeigersinn relativ zu A steht)
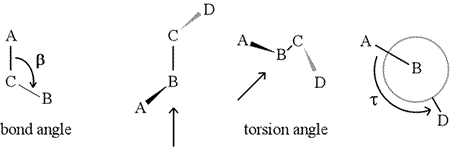
Natürlich können andere Atome an B und C gebunden sein – und sind es in der Regel auch. Wir müssten angeben, welche Atome A, B, C und D entsprechen, um den Flächenwinkel eindeutig zu definieren. Bei langen, unverzweigten Polymeren, wie z. B. Proteinen, ist es sinnvoll, dass A bis D alle Atome der Hauptkette sind. Nachstehend finden Sie eine Molekülgrafik, die der obigen Skizze entspricht und die Definition des Polypeptid-Hauptketten-Dihedralwinkels Phi (φ) veranschaulicht.
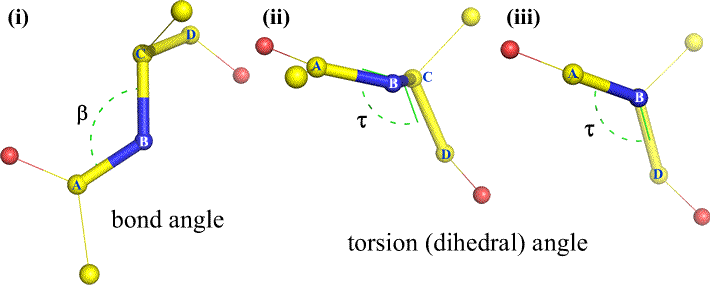
Polypeptid-Hauptketten-Dihedralwinkel: Phi (φ), Psi (ψ) und Omega (ω)
Ein Flächenwinkel wird durch vier Atome definiert. Er kann visualisiert werden, indem man die zentrale Bindung (d. h. die Bindung von Atom 2 zu Atom 3) betrachtet. Es gibt drei Arten von Flächenwinkeln entlang einer Polypeptidkette:
Phi (φ) – zentrale Bindung zwischen N(i) und C(alpha, i) . Schauen Sie sich die N(i)-Cα(i)-Bindung an und beachten Sie den Winkel, den das Acylkohlenstoffatom C(i) relativ zu C(i-1) – dem Acylkohlenstoffatom des vorhergehenden Restes – einnimmt.
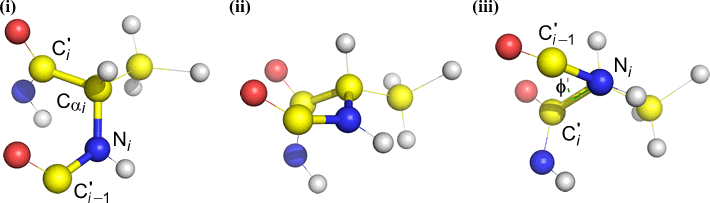
Psi (ψ) – zentrale Bindung zwischen C(alpha, i) und C(i) . Schauen Sie sich die Cα(i)-C(i)-Bindung an und beachten Sie den Winkel, den N(i + 1) relativ zu N(i) einnimmt.
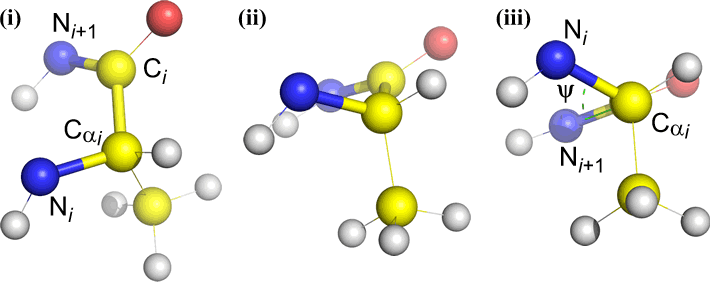
Omega (ω) – die Peptidbindung zwischen dem Acylkohlenstoff C(i) und N(i+1) ist die zentrale Bindung.
Phi (φ) und psi (ψ) werden manchmal als Ramachandran-Winkel bezeichnet, da sie in einem zweidimensionalen Diagramm der Hauptketten-Dihedralwinkel, dem Ramachandran-Diagramm, verwendet werden (siehe unten).
Ramachandran-Diagramm
Das Ramachandran-Diagramm ist ein Diagramm der Hauptketten-Dihedralwinkel phi (φ) und psi (ψ) für eine Polypeptidkette, mit phi (φ)-Werten entlang der x-Achse und psi (ψ)-Werten entlang der y-Achse.
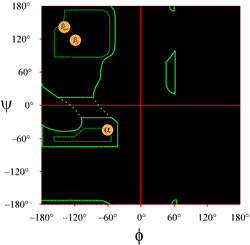
Das Layout eines Ramachandran-Diagramms, wie es typischerweise in Lehrbüchern dargestellt wird, ist links abgebildet (klicken Sie auf die Abbildung, um eine größere Version anzuzeigen). Die Konturen zeigen das Ausmaß der erlaubten (hellgrün) und der am meisten bevorzugten (dunkelgrün) Kombinationen von (φ, ψ). Die orangefarbenen Kreise zeigen die Lage der idealen phi- und psi-Werte für die häufigsten regelmäßigen Sekundärstrukturmerkmale, die beta-Stränge (in antiparallelen und parallelen Schichten) und die alpha-Helices. Außerhalb der Kreise sind die entsprechenden Konformationen ungünstig oder nicht zulässig. Die genaue Lage der Konturen sollte nicht zu wörtlich genommen werden, da die günstigen und zulässigen Regionen von der Identität der Reste abhängen. Insbesondere Glycin hat viel größere erlaubte Bereiche als hier gezeigt. Dies wird weiter unten erörtert.
Ein „echter“ Ramachandran-Plot
Im „Endspiel“ der Proteinstrukturbestimmung muss das experimentell ermittelte Modell auf seine stereochemische Qualität hin analysiert werden. Ernsthafte Probleme mit dem Modell können sich ergeben, wenn es Nicht-Gly-Reste gibt, deren Hauptketten-Dihedralwinkel außerhalb der zulässigen Regionen liegen, oder wenn ein zu hoher Anteil der Reste außerhalb der bevorzugten Region liegt. Ein Beispiel für ein Ramachandran-Diagramm für ein Protein mit 190 Resten ist in der nebenstehenden Abbildung dargestellt.
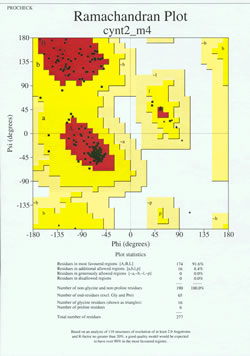
Die Abbildung zeigt ein Ramachandran-Diagramm für eine durch Röntgenkristallographie bestimmte Proteinstruktur. (Klicken Sie darauf, um eine größere Version in einem neuen Fenster anzuzeigen.) Jedes schwarze Quadrat stellt die Konformation der Hauptkette an einem Rest des Proteins dar. Beachten Sie, wie sich die phi, psi-Werte für die Reste in den roten „bevorzugten“ Regionen anhäufen. Der rote Bereich oben links (in der Abbildung mit „B“ bezeichnet) entspricht den Resten in einer Beta-Strang-Konformation der Hauptkette, während der große Bereich in der Mitte (mit „A“ bezeichnet) der Alpha-Helix entspricht. Der dritte, kleine rote Bereich des Diagramms zeigt die Reste, die eine linkshändige („L“) Alpha-Helix annehmen, an. Einige der Reste liegen in „zusätzlichen erlaubten Regionen“ (hellgelb), die an die bevorzugten Regionen angrenzen. Beachten Sie, dass die Glycinreste (als Dreiecke dargestellt) in einigen Fällen in „verbotenen Regionen“ liegen. Das liegt daran, dass Gly mit nur dem kleinen Wasserstoffatom als „Seitenkette“ sterisch viel weniger belastet ist als andere Aminosäuren. Gly ist in der Lage, Winkelpaare von phi und psi einzunehmen, die für andere Reste nicht zulässig sind.