Hyperbolisk tangent: Introduktion till den hyperboliska tangentfunktionen

Introduktion till den hyperboliska tangentfunktionen

Definition av den hyperboliska tangentfunktionen

Den hyperboliska tangentfunktionen är en gammal matematisk funktion. Den användes för första gången i ett arbete av L’Abbe Sauri (1774).

Denna funktion kan enkelt definieras som förhållandet mellan de hyperboliska sinus- och cosinusfunktionerna (eller expanderat, som förhållandet mellan halvdifferensen och halvsumman av två exponentialfunktioner i punkterna och ):

Efter jämförelse med de berömda Eulerformlerna för sinus- och cosinusfunktionerna, och , är det lätt att härleda följande representation av den hyperboliska tangenten genom den cirkulära tangentfunktionen:

Denna formel gör det möjligt att härleda alla egenskaper och formler för den hyperboliska tangenten från motsvarande egenskaper och formler för cirkeltangenten.

En snabb titt på den hyperboliska tangentfunktionen

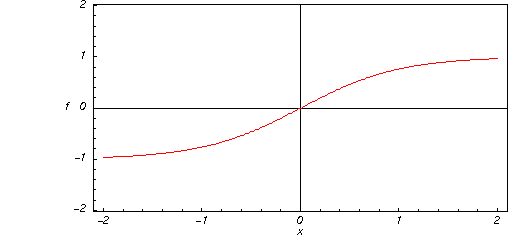
Här är en grafisk bild av den hyperboliska tangentfunktionen för reella värden av dess argument .

Representation genom mer generella funktioner

Den hyperboliska tangentfunktionen kan representeras med hjälp av mer allmänna matematiska funktioner. Som kvoten mellan de hyperboliska sinus- och cosinusfunktionerna som är specialfall av de generaliserade hypergeometriska funktionerna, Bessel-, Struve- och Mathieu-funktionerna, kan den hyperboliska tangentfunktionen också representeras som kvoten mellan dessa specialfunktioner. Men dessa representationer är inte särskilt användbara. Det är mer användbart att skriva den hyperboliska tangentfunktionen som särskilda fall av en specialfunktion. Detta kan göras med hjälp av dubbelt periodiska Jacobi elliptiska funktioner som degenererar till den hyperboliska tangentfunktionen när deras andra parameter är lika med eller :

Definition av den hyperboliska tangentfunktionen för ett komplext argument

I det komplexa planet definieras funktionen med samma formel som används för reella värden:

I punkterna , där har nollor, är nämnaren i den sista formeln lika med noll och har singulariteter (poler av första ordningen).

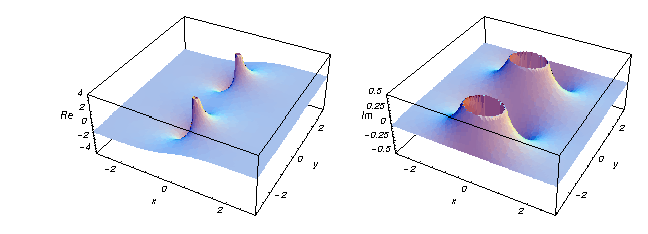
Här är två grafer som visar real- och imaginärdelen av den hyperboliska tangentfunktionen över det komplexa planet.

De mest kända egenskaperna och formlerna för den hyperboliska tangentfunktionen

Värden i punkter

Värdena för den hyperboliska tangenten för speciella värden på dess argument kan lätt härledas från motsvarande värden för cirkeltangenten i cirkelns speciella punkter:

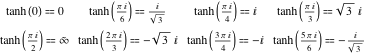
Värdena vid oändligheten kan uttryckas med följande formler:

Allmänna egenskaper

För verkliga värden av argumentet är värdena av verkliga.

I punkterna är värdena för algebraiska. I flera fall kan de vara , 0 eller ⅈ:

Värdena av kan uttryckas endast med hjälp av kvadratrötter om och är en produkt av en potens av 2 och distinkta Fermat-primtal {3, 5, 17, 257, …}.

Funktionen är en analytisk funktion av som är definierad över hela det komplexa -planet och som inte har grenklipp och grenpunkter. Den har en oändlig mängd singulära punkter:

(a) är de enkla polerna med residualerna 1.(b) är en essentiell singulär punkt.

Den är en periodisk funktion med perioden :

Funktionen är en udda funktion med spegelsymmetri:

Differentiering

Den första derivatan av har enkla representationer med hjälp av antingen funktionen eller funktionen :

Den derivatan av har mycket mer komplicerade representationer än de symboliska derivatorerna för och :

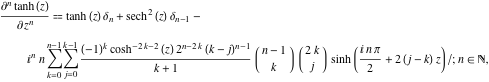
där är Kroneckerdeltasymbolen: och .

Ordinär differentialekvation

Funktionen uppfyller följande icke-linjära differentialekvation av första ordningen:

Serieframställning

Funktionen har en enkel serieexpansion vid ursprunget som konvergerar för alla ändliga värden med :

där är Bernoullitalen.

Integralrepresentation

Funktionen har en välkänd integralrepresentation genom följande bestämda integral längs den positiva delen av den reella axeln:

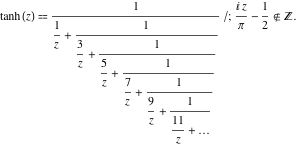
Fortsatta bråkrepresentationer

Funktionen har följande enkla fortsatta bråkrepresentationer:

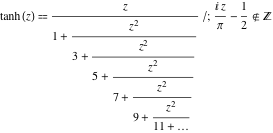
Indefinit integration

Indefinita integraler av uttryck som involverar den hyperboliska tangentfunktionen kan ibland uttryckas med hjälp av elementära funktioner. Ofta behövs dock speciella funktioner för att uttrycka resultaten även när integranterna har en enkel form (om de kan utvärderas i sluten form). Här är några exempel:

Definitiv integration

Definita integraler som innehåller den hyperboliska tangentfunktionen är ibland enkla. Till exempel kan den berömda katalanska konstanten definieras genom följande integral:

En del specialfunktioner kan användas för att utvärdera mer komplicerade bestämda integraler. Till exempel behövs den hypergeometriska funktionen för att uttrycka följande integral:

Slutlig summering

Följande finita summa som innehåller den hyperboliska tangentfunktionen kan uttryckas med hjälp av hyperboliska kotangentfunktioner:

Additionsformler

Den hyperboliska tangenten till en summa kan representeras med regeln: ”Den hyperboliska tangenten till en summa är lika med summan av de hyperboliska tangenterna dividerad med ett plus produkten av de hyperboliska tangenterna”. En liknande regel gäller för differensens hyperboliska tangent:

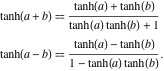
Flera argument

I fallet med flera argument , , …, kan funktionen representeras som förhållandet mellan de finita summorna som inkluderar potenser av hyperboliska tangenter:

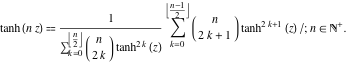
Formler för halva vinklar

Den hyperboliska tangenten till en halvvinkel kan representeras med hjälp av två hyperboliska funktioner genom följande enkla formler:

Den hyperboliska sinusfunktionen i den sista formeln kan ersättas med den hyperboliska cosinusfunktionen. Men det leder till en mer komplicerad representation som är giltig i en horisontell remsa:

De sista restriktionerna kan tas bort genom att ändra formeln något (nu är identiteten giltig för alla komplexa ):

Summor av två direkta funktioner

Summan av två hyperboliska tangentfunktioner kan beskrivas med regeln: ”Summan av hyperboliska tangenter är lika med summan av summarens hyperboliska sinus multiplicerad med de hyperboliska sekanterna”. En liknande regel gäller för differensen av två hyperboliska tangenter:

Produkter som involverar den direkta funktionen

Produkten av två hyperboliska tangentfunktioner och produkten av den hyperboliska tangenten och kotangenten har följande representationer:

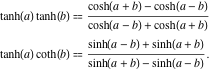
Olikheter

Den mest kända olikheten för den hyperboliska tangentfunktionen är följande:

Samband med dess omvända funktion

Det finns enkla samband mellan funktionen och dess omvända funktion :

Den andra formeln gäller åtminstone i den horisontella remsan . Utanför denna remsa gäller en mycket mer komplicerad relation (som innehåller enhetstrappan, realdelen och golvfunktionerna):