Tangente hyperbolique : Introduction à la fonction tangente hyperbolique

Introduction à la fonction tangente hyperbolique

Définition de la fonction tangente hyperbolique

La fonction tangente hyperbolique est une fonction mathématique ancienne. Elle a été utilisée pour la première fois dans l’ouvrage de l’abbé Sauri (1774).

Cette fonction est facilement définie comme le rapport entre les fonctions sinus et cosinus hyperboliques (ou étendue, comme le rapport de la demi-différence et de la demi-somme de deux fonctions exponentielles aux points et ) :

Après comparaison avec les célèbres formules d’Euler pour les fonctions sinus et cosinus, et , il est facile de déduire la représentation suivante de la tangente hyperbolique par la fonction tangente circulaire :

Cette formule permet de dériver toutes les propriétés et formules de la tangente hyperbolique à partir des propriétés et formules correspondantes de la tangente circulaire.

Un coup d’œil rapide sur la fonction tangente hyperbolique

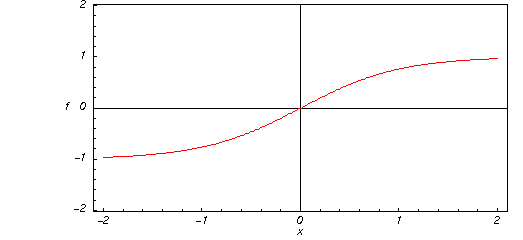
Voici un graphique de la fonction tangente hyperbolique pour des valeurs réelles de son argument .

Représentation par des fonctions plus générales

La fonction tangente hyperbolique peut être représentée en utilisant des fonctions mathématiques plus générales. En tant que rapport des fonctions sinus et cosinus hyperboliques qui sont des cas particuliers des fonctions hypergéométriques, de Bessel, de Struve et de Mathieu généralisées, la fonction tangente hyperbolique peut aussi être représentée par des rapports de ces fonctions spéciales. Mais ces représentations ne sont pas très utiles. Il est plus utile d’écrire la fonction tangente hyperbolique comme des cas particuliers d’une fonction spéciale. Cela peut être fait en utilisant des fonctions elliptiques de Jacobi doublement périodiques qui dégénèrent en fonction tangente hyperbolique lorsque leur second paramètre est égal à ou :

Définition de la fonction tangente hyperbolique pour un argument complexe

Dans le plan complexe, la fonction est définie par la même formule que celle utilisée pour les valeurs réelles :

En les points , où a des zéros, le dénominateur de la dernière formule est égal à zéro et présente des singularités (pôles du premier ordre).

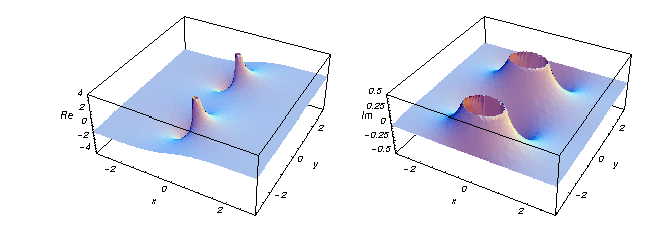
Voici deux graphiques montrant les parties réelles et imaginaires de la fonction tangente hyperbolique sur le plan complexe.

Les propriétés et formules les plus connues de la fonction tangente hyperbolique

Valeurs en points

Les valeurs de la tangente hyperbolique pour des valeurs particulières de son argument peuvent être facilement dérivées des valeurs correspondantes de la tangente circulaire en des points particuliers du cercle :

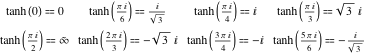
Les valeurs à l’infini peuvent être exprimées par les formules suivantes :

Caractéristiques générales

Pour des valeurs réelles de l’argument , les valeurs de sont réelles.

Dans les points , les valeurs de sont algébriques. Dans plusieurs cas, elles peuvent être , 0, ou ⅈ:

Les valeurs de peuvent être exprimées en utilisant uniquement des racines carrées si et est un produit d’une puissance de 2 et de nombres premiers de Fermat distincts {3, 5, 17, 257, …}.

La fonction est une fonction analytique de qui est définie sur l’ensemble du plan complexe et qui n’a pas de coupes et de points de branche. Elle possède un ensemble infini de points singuliers :

(a) sont les pôles simples avec les résidus 1.(b) est un point singulier essentiel.

C’est une fonction périodique de période :

La fonction est une fonction impaire à symétrie miroir :

Différenciation

La dérivée première de a des représentations simples utilisant soit la fonction soit la fonction :

La dérivée de a des représentations beaucoup plus compliquées que les dérivées symboliques pour et :

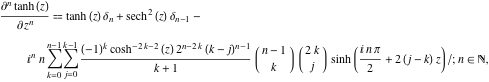
où est le symbole delta de Kronecker : et .

Équation différentielle ordinaire

La fonction satisfait l’équation différentielle non linéaire du premier ordre suivante :

Représentation en série

La fonction a un développement en série simple à l’origine qui converge pour toutes les valeurs finies avec :

où sont les nombres de Bernoulli.

Représentation intégrale

La fonction a une représentation intégrale bien connue par l’intégrale définie suivante le long de la partie positive de l’axe réel:

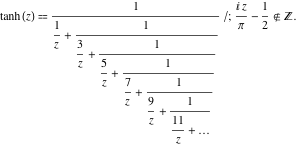
Représentations de fractions continues

La fonction a les représentations de fractions continues simples suivantes :

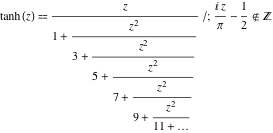
Intégration indéfinie

Les intégrales indéfinies d’expressions impliquant la fonction tangente hyperbolique peuvent parfois être exprimées à l’aide de fonctions élémentaires. Cependant, des fonctions spéciales sont fréquemment nécessaires pour exprimer les résultats même lorsque les intégrandes ont une forme simple (si elles peuvent être évaluées sous forme fermée). Voici quelques exemples:

Intégration définie

Les intégrales définies qui contiennent la fonction tangente hyperbolique sont parfois simples. Par exemple, la célèbre constante catalane peut être définie par l’intégrale suivante :

Certaines fonctions spéciales peuvent être utilisées pour évaluer des intégrales définies plus compliquées. Par exemple, la fonction hypergéométrique est nécessaire pour exprimer l’intégrale suivante :

Somme finie

La somme finie suivante qui contient la fonction tangente hyperbolique peut être exprimée en utilisant les fonctions cotangentes hyperboliques :

Formules d’addition

La tangente hyperbolique d’une somme peut être représentée par la règle : « la tangente hyperbolique d’une somme est égale à la somme des tangentes hyperboliques divisée par un plus le produit des tangentes hyperboliques ». Une règle similaire est valable pour la tangente hyperbolique de la différence:

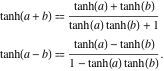
Arguments multiples

Dans le cas d’arguments multiples , , …, la fonction peut être représentée comme le rapport des sommes finies qui inclut les puissances des tangentes hyperboliques :

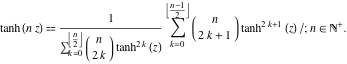
Formules de demi-angle

La tangente hyperbolique d’un demi-angle peut être représentée à l’aide de deux fonctions hyperboliques par les formules simples suivantes :

La fonction sinus hyperbolique dans la dernière formule peut être remplacée par la fonction cosinus hyperbolique. Mais cela conduit à une représentation plus compliquée qui est valable dans une bande horizontale:

Les dernières restrictions peuvent être supprimées en modifiant légèrement la formule (maintenant l’identité est valable pour tous les complexes) :

Somme de deux fonctions directes

La somme de deux fonctions tangentes hyperboliques peut être décrite par la règle : « la somme des tangentes hyperboliques est égale au sinus hyperbolique de la somme multiplié par les sécantes hyperboliques ». Une règle similaire est valable pour la différence de deux tangentes hyperboliques :

Produits faisant intervenir la fonction directe

Le produit de deux fonctions tangentes hyperboliques et le produit de la tangente et de la cotangente hyperboliques ont les représentations suivantes :

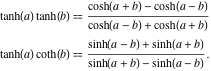
Inégalités

L’inégalité la plus célèbre pour la fonction tangente hyperbolique est la suivante :

Relations avec sa fonction inverse

Il existe des relations simples entre la fonction et sa fonction inverse :

La deuxième formule est valable au moins dans la bande horizontale . En dehors de cette bande, une relation beaucoup plus compliquée (qui contient le pas unitaire, la partie réelle et les fonctions plancher) tient: