Hyperbolisk tangent: Introduktion til den hyperbolske tangentfunktion

Introduktion til den hyperbolske tangentfunktion

Definition af den hyperbolske tangentfunktion

Den hyperbolske tangentfunktion er en gammel matematisk funktion. Den blev første gang anvendt i et værk af L’Abbe Sauri (1774).

Denne funktion kan let defineres som forholdet mellem den hyperbolske sinus- og cosinusfunktion (eller udvidet, som forholdet mellem halvdifferencen og halvsummen af to eksponentielle funktioner i punkterne og ):

Efter sammenligning med de berømte Euler-formler for sinus- og cosinusfunktionen, og , er det let at udlede følgende repræsentation af den hyperbolske tangent gennem den cirkulære tangentfunktion:

Denne formel gør det muligt at udlede alle egenskaber og formler for den hyperbolske tangent fra de tilsvarende egenskaber og formler for den cirkulære tangent.

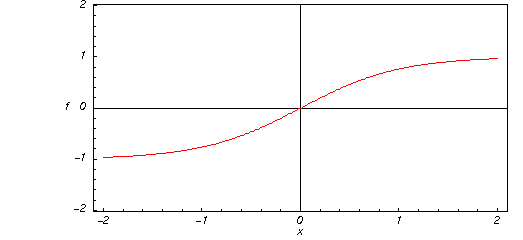
Et hurtigt kig på den hyperbolske tangentfunktion

Her er en grafisk fremstilling af den hyperbolske tangentfunktion for reelle værdier af dens argument .

Repræsentation ved hjælp af mere generelle funktioner

Den hyperbolske tangentfunktion kan repræsenteres ved hjælp af mere generelle matematiske funktioner. Som forholdet mellem de hyperbolske sinus- og cosinusfunktioner, der er særlige tilfælde af de generaliserede hypergeometriske funktioner, Bessel-, Struve- og Mathieu-funktioner, kan den hyperbolske tangentfunktion også repræsenteres som forhold mellem disse særlige funktioner. Men disse repræsentationer er ikke særlig nyttige. Det er mere nyttigt at skrive den hyperbolske tangentfunktion som særlige tilfælde af én speciel funktion. Det kan gøres ved hjælp af dobbeltperiodiske jacobi-elliptiske funktioner, der degenererer til den hyperbolske tangentfunktion, når deres anden parameter er lig med eller :

Definition af den hyperbolske tangentfunktion for et komplekst argument

I den komplekse plan er funktionen defineret ved den samme formel, som anvendes for reelle værdier:

I punkterne , hvor har nuller, er nævneren i den sidste formel lig med nul, og har singulariteter (poler af første orden).

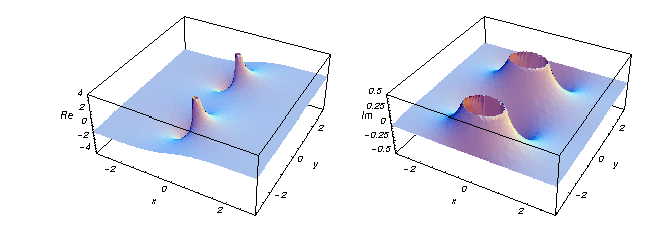
Her er to grafer, der viser den reelle og imaginære del af den hyperbolske tangentfunktion over det komplekse plan.

De bedst kendte egenskaber og formler for den hyperbolske tangentfunktion

Værdier i punkter

Værdierne af den hyperbolske tangent for særlige værdier af dens argument kan let udledes af de tilsvarende værdier af den cirkulære tangent i de særlige punkter på cirklen:

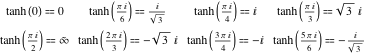
Værdierne i uendelighed kan udtrykkes ved følgende formler:

Generelle egenskaber

For reelle værdier af argumentet , er værdierne af reelle.

I punkterne er værdierne af algebraiske. I flere tilfælde kan de være , 0 eller ⅈ:

Værdierne af kan kun udtrykkes ved hjælp af kvadratrødder, hvis og er et produkt af en potens af 2 og forskellige Fermat-præmier {3, 5, 17, 257, …}.

Funktionen er en analytisk funktion af , der er defineret over hele den komplekse -plan, og som ikke har forgreningsskæringer og forgreningspunkter. Den har et uendeligt sæt af singulære punkter:

(a) er de simple poler med restværdien 1.(b) er et essentielt singulært punkt.

Den er en periodisk funktion med perioden :

Funktionen er en ulige funktion med spejlsymmetri:

Differentiering

Den første afledte af har simple repræsentationer ved hjælp af enten -funktionen eller -funktionen:

Den afledte af har meget mere komplicerede repræsentationer end de symbolske afledte for og :

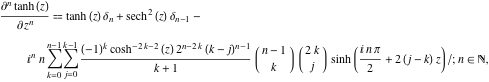
hvor er Kronecker-delta-symbolet: og .

Ordinær differentialligning

Funktionen opfylder følgende ikke-lineære differentialligning af første orden:

Seriefremstilling

Funktionen har en simpel serieudvidelse ved oprindelsen, der konvergerer for alle finitte værdier med :

hvor er Bernoulli-tallene.

Integralfremstilling

Funktionen har en velkendt integralfremstilling gennem følgende definitte integral langs den positive del af den reelle akse:

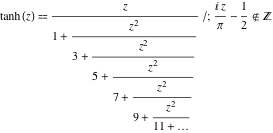
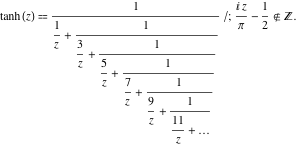
Fortsatte brøkfremstillinger

Funktionen har følgende simple fortsatte brøkfremstillinger:

Ubestemt integration

Ubestemte integraler af udtryk, der involverer den hyperbolske tangentfunktion, kan undertiden udtrykkes ved hjælp af elementære funktioner. Der er dog ofte behov for specielle funktioner for at udtrykke resultaterne, selv når integranderne har en simpel form (hvis de kan evalueres i lukket form). Her er nogle eksempler:

Bestemt integration

Definitte integraler, der indeholder den hyperbolske tangentfunktion, er nogle gange simple. For eksempel kan den berømte catalanske konstant defineres ved hjælp af følgende integral:

Nogle specielle funktioner kan bruges til at evaluere mere komplicerede definitte integraler. For eksempel er den hypergeometriske funktion nødvendig for at udtrykke følgende integral:

Endelig summering

Den følgende endelige sum, der indeholder den hyperbolske tangentfunktion, kan udtrykkes ved hjælp af hyperbolske cotangentfunktioner:

Additionsformler

Den hyperbolske tangent til en sum kan repræsenteres ved reglen: “den hyperbolske tangent til en sum er lig med summen af de hyperbolske tangenter divideret med et plus produktet af de hyperbolske tangenter”. En lignende regel gælder for differencens hyperboliske tangent:

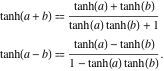
Flere argumenter

I tilfælde af flere argumenter , , …, kan funktionen repræsenteres som forholdet mellem de finitte summer, der omfatter potenser af hyperboliske tangenter:

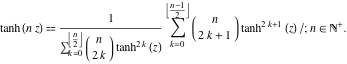
Halvvvinkelformler

Den hyperbolske tangent til en halv vinkel kan repræsenteres ved hjælp af to hyperboliske funktioner ved følgende enkle formler:

Den hyperbolske sinusfunktion i den sidste formel kan erstattes med den hyperbolske cosinusfunktion. Men det fører til en mere kompliceret fremstilling, der er gyldig i en vandret stribe:

De sidste begrænsninger kan fjernes ved at ændre formlen en smule (nu er identiteten gyldig for alle komplekse ):

Summen af to direkte funktioner

Summen af to hyperboliske tangentfunktioner kan beskrives ved reglen: “summen af hyperboliske tangenter er lig med den hyperboliske sinus af summen multipliceret med de hyperboliske sekanter”. En lignende regel gælder for forskellen af to hyperboliske tangenter:

Produkter, der involverer den direkte funktion

Produktet af to hyperboliske tangentfunktioner og produktet af den hyperboliske tangent og kotangenten har følgende repræsentationer:

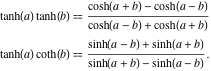
Uligheder

Den mest berømte ulighed for den hyperbolske tangentfunktion er følgende:

Sammenhænge med dens omvendte funktion

Der er enkle sammenhænge mellem funktionen og dens omvendte funktion :

Den anden formel gælder i det mindste i den vandrette strimmel . Uden for denne stribe gælder en meget mere kompliceret relation (der indeholder enhedstrinnet, realdelen og gulvfunktionerne):