Tangente hiperbólica: Introducción a la función tangente hiperbólica

Introducción a la función tangente hiperbólica

Definición de la función tangente hiperbólica

La función tangente hiperbólica es una función matemática antigua. Fue utilizada por primera vez en la obra de L’Abbe Sauri (1774).

Esta función se define fácilmente como la relación entre las funciones seno y coseno hiperbólicas (o ampliada, como la relación de la semidiferencia y la semisuma de dos funciones exponenciales en los puntos y ):

Tras la comparación con las famosas fórmulas de Euler para las funciones seno y coseno, y , es fácil derivar la siguiente representación de la tangente hiperbólica mediante la función tangente circular:

Esta fórmula permite derivar todas las propiedades y fórmulas de la tangente hiperbólica a partir de las correspondientes propiedades y fórmulas de la tangente circular.

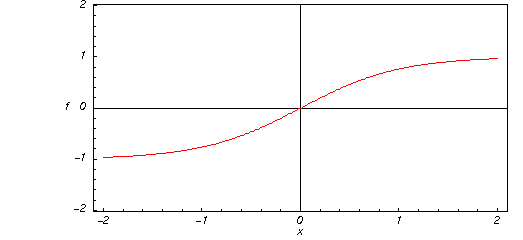
Un vistazo rápido a la función tangente hiperbólica

Aquí tenemos una gráfica de la función tangente hiperbólica para valores reales de su argumento .

Representación mediante funciones más generales

La función tangente hiperbólica puede representarse mediante funciones matemáticas más generales. Como cociente de las funciones hiperbólicas seno y coseno que son casos particulares de las funciones hipergeométricas generalizadas, de Bessel, de Struve y de Mathieu, la función tangente hiperbólica también puede representarse como cocientes de esas funciones especiales. Pero estas representaciones no son muy útiles. Es más útil escribir la función tangente hiperbólica como casos particulares de una función especial. Eso puede hacerse utilizando funciones elípticas de Jacobi doblemente periódicas que degeneran en la función tangente hiperbólica cuando su segundo parámetro es igual a o :

Definición de la función tangente hiperbólica para un argumento complejo

En el plano complejo , la función se define por la misma fórmula que se utiliza para valores reales:

En los puntos , donde tiene ceros, el denominador de la última fórmula es igual a cero y tiene singularidades (polos de primer orden).

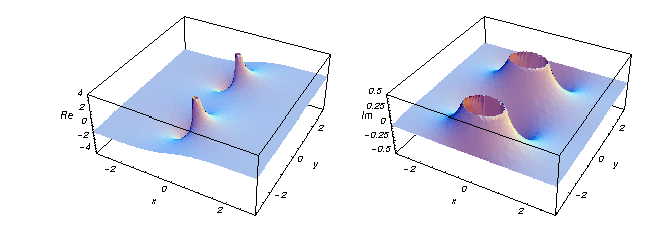
Aquí tienes dos gráficas que muestran las partes real e imaginaria de la función tangente hiperbólica sobre el plano complejo.

Las propiedades y fórmulas más conocidas de la función tangente hiperbólica

Valores en puntos

Los valores de la tangente hiperbólica para valores especiales de su argumento pueden derivarse fácilmente de los valores correspondientes de la tangente circular en los puntos especiales del círculo:

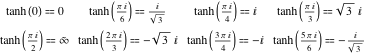
Los valores en el infinito se pueden expresar mediante las siguientes fórmulas:

Características generales

Para valores reales del argumento , los valores de son reales.

En los puntos , los valores de son algebraicos. En varios casos, pueden ser , 0, o ⅈ:

Los valores de pueden expresarse usando sólo raíces cuadradas si y es un producto de una potencia de 2 y distintos primos de Fermat {3, 5, 17, 257, …}.

La función es una función analítica de que está definida sobre todo el complejo -plano y no tiene cortes ni puntos de ramificación. Tiene un conjunto infinito de puntos singulares:

(a) son los polos simples con residuos 1.(b) es un punto singular esencial.

Es una función periódica con periodo :

La función es una función impar con simetría especular:

Diferenciación

La primera derivada de tiene representaciones sencillas utilizando la función o la función :

La derivada de tiene representaciones mucho más complicadas que las derivadas simbólicas para y :

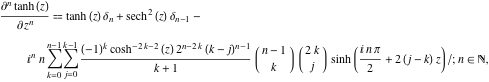
donde es el símbolo delta de Kronecker: y .

Ecuación diferencial ordinaria

La función satisface la siguiente ecuación diferencial no lineal de primer orden:

Representación en serie

La función tiene una expansión en serie simple en el origen que converge para todos los valores finitos con :

donde son los números de Bernoulli.

Representación integral

La función tiene una representación integral bien conocida a través de la siguiente integral definida a lo largo de la parte positiva del eje real:

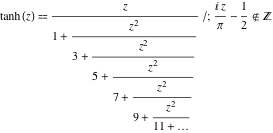
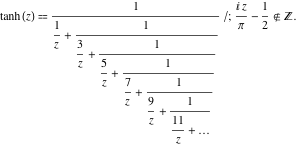
Representaciones de fracciones continuas

La función tiene las siguientes representaciones de fracciones continuas simples:

Integración indefinida

Las integrales indefinidas de expresiones que implican la función tangente hiperbólica pueden expresarse a veces utilizando funciones elementales. Sin embargo, con frecuencia se necesitan funciones especiales para expresar los resultados incluso cuando los integrados tienen una forma sencilla (si es que pueden evaluarse en forma cerrada). He aquí algunos ejemplos:

Integración definida

Las integrales definidas que contienen la función tangente hiperbólica son a veces simples. Por ejemplo, la famosa constante catalana puede definirse mediante la siguiente integral:

Algunas funciones especiales pueden utilizarse para evaluar integrales definidas más complicadas. Por ejemplo, la función hipergeométrica es necesaria para expresar la siguiente integral:

Suma finita

La siguiente suma finita que contiene la función tangente hiperbólica puede expresarse utilizando funciones cotangentes hiperbólicas:

Fórmulas de adición

La tangente hiperbólica de una suma puede representarse mediante la regla: «la tangente hiperbólica de una suma es igual a la suma de las tangentes hiperbólicas dividida por uno más el producto de las tangentes hiperbólicas». Una regla similar es válida para la tangente hiperbólica de la diferencia:

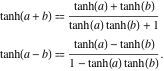
Argumentos múltiples

En el caso de argumentos múltiples , , …, la función puede representarse como el cociente de las sumas finitas que incluyen potencias de tangentes hiperbólicas:

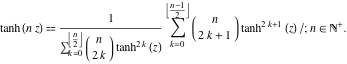
Fórmulas de medio ángulo

La tangente hiperbólica de un medio ángulo puede representarse utilizando dos funciones hiperbólicas mediante las siguientes fórmulas simples:

La función seno hiperbólico de la última fórmula puede sustituirse por la función coseno hiperbólico. Pero lleva a una representación más complicada que es válida en una franja horizontal:

Las últimas restricciones se pueden eliminar modificando ligeramente la fórmula (ahora la identidad es válida para todo el complejo ):

Sumas de dos funciones directas

La suma de dos funciones tangentes hiperbólicas puede describirse mediante la regla: «la suma de tangentes hiperbólicas es igual al seno hiperbólico de la suma multiplicado por las secantes hiperbólicas». Una regla similar es válida para la diferencia de dos tangentes hiperbólicas:

Los productos que implican la función directa

El producto de dos funciones tangentes hiperbólicas y el producto de la tangente hiperbólica y la cotangente tienen las siguientes representaciones:

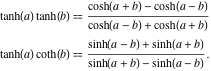
Inecuaciones

La desigualdad más famosa para la función tangente hiperbólica es la siguiente:

Relaciones con su función inversa

Hay relaciones sencillas entre la función y su función inversa :

La segunda fórmula es válida al menos en la franja horizontal . Fuera de esta franja se mantiene una relación mucho más complicada (que contiene el escalón unitario, la parte real y las funciones suelo):