Ledningsevne af iboende halvledere
Ledningsevnen (σ) er produktet af antallet af ladningstrækninger (n eller p), deres ladning (e) og deres mobilitet (µ). Husk fra kapitel 6, at µ er forholdet mellem ladningsbærernes driftshastighed og det elektriske felt og har enheder i cm2/Volt-sekund. Typisk har elektroner og huller lidt forskellige mobiliteter (henholdsvis µe og µh), så ledningsevnen er givet ved:
\
For begge typer ladningsbærere husker vi fra kapitel 6, at mobiliteten μ er givet ved:
\
hvor e er den grundlæggende enhed for ladning, τ er spredningstiden og m er ladningsbærerens effektive masse.
Tager man et gennemsnit af elektron- og hulmobiliteten og bruger n = p, får man
\
Gennem måling af ledningsevnen som en funktion af temperaturen er det muligt at få aktiveringsenergien for ledning, som er Egap/2. Denne form for plot, der ligner et Arrhenius-plot, er vist til højre for tre forskellige udopede halvledere. Hældningen af linjen er i hvert tilfælde -Egap/2k.
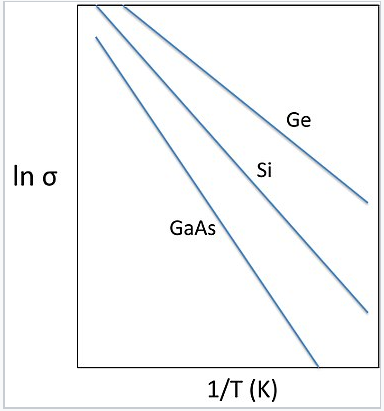
Plots af ln(σ) vs. omvendt temperatur for de intrinsiske halvledere Ge (Egap = 0,7 eV), Si (1,1 eV) og GaAs (1,4 eV). Hældningen af linjen er -Egap/2k.
Doping af halvledere. Næsten alle anvendelser af halvledere indebærer kontrolleret dotering, dvs. udskiftning af urenhedsatomer i gitteret. Meget små mængder af doteringsstoffer (i del-per-million-området) påvirker halvledernes ledningsevne dramatisk. Derfor er der behov for meget rene halvledermaterialer, der er omhyggeligt doteret – både med hensyn til koncentrationen og den rumlige fordeling af urenhedsatomer –
n- og p-type-doping. I krystallinsk Si har hvert atom fire valenselektroner og laver fire bindinger til sine naboer. Dette er præcis det rigtige antal elektroner til at fylde halvlederens valensbånd fuldstændigt ud. Ved at indføre et fosforatom i gitteret (det positivt ladede atom i figuren til højre) tilføjes der en ekstra elektron, fordi P har fem valenselektroner og kun har brug for fire til at binde sig til sine naboer. Den ekstra elektron er ved lav temperatur bundet til fosforatomet i en hydrogenlignende molekylær orbital, der er meget større end 3s orbitalet for et isoleret P-atom på grund af halvlederens høje dielektriske konstant. I silicium er denne “udvidede” Bohr-radius ca. 42 Å, dvs. 80 gange større end i hydrogenatomet. Den energi, der er nødvendig for at ionisere denne elektron – for at lade den bevæge sig frit i gitteret – er kun ca. 40-50 meV, hvilket ikke er meget større end den termiske energi (26 meV) ved stuetemperatur. Fermi-niveauet ligger derfor lige under ledningsbåndskanten, og en stor del af disse ekstra elektroner fremmes til ledningsbåndet ved stuetemperatur, idet de efterlader faste positive ladninger på P-atompladserne. Krystallet er n-dopet, hvilket betyder, at flertalsbæreren (elektronen) er negativt ladet.
Alternativt kan bor erstattes af silicium i gitteret, hvilket resulterer i p-type-doping, hvor flertalsbæreren (hullet) er positivt ladet. Bor har kun tre valenselektroner og “låner” en fra Si-gitteret, hvilket skaber et positivt ladet hul, der findes i en stor hydrogenlignende orbital omkring B-atomet. Dette hul kan blive delokaliseret ved at fremme en elektron fra valensbåndet til at fylde den lokaliserede hultilstand. Denne proces kræver igen kun 40-50 meV, så ved stuetemperatur findes en stor del af de huller, der indføres ved bor-doping, i delokaliserede valensbåndstilstande. Fermi-niveauet (det elektronenerginiveau, der har en 50% sandsynlighed for besættelse ved nul temperatur) ligger lige over valensbåndskanten i en p-type halvleder.
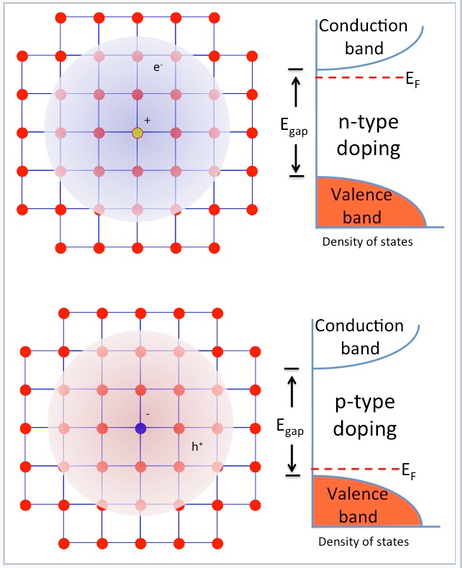
n- og p-type-doping af halvledere indebærer substitution af elektrondonoratomer (lys orange) eller acceptoratomer (blå) i gitteret. Disse udskiftninger indfører henholdsvis ekstra elektroner eller huller, som let ioniseres af termisk energi og bliver til frie bærere. Fermi-niveauet for en doteret halvleder ligger nogle få tiendedele mV under ledningsbåndet (n-type) eller over valensbåndet (p-type).
Som nævnt ovenfor ændrer doteringen af halvledere dramatisk deres ledningsevne. For eksempel er den intrinsiske ladningskoncentration i Si ved 300 K ca. 1010 cm-3. Massevirkningsligevægten for elektroner og huller gælder også for doterede halvledere, så vi kan skrive:
\
Hvis vi erstatter Si med P på niveauet en del pr. million, er elektronkoncentrationen ca. 1016 cm-3, da der er ca. 1022 Si-atomer/cm3 i krystallen. Ifølge massevirkningsligningen gælder det, at hvis n = 1016, så er p = 104 cm-3. Der er tre konsekvenser af denne beregning:
- Tætheden af ladningsbærere i den doterede halvleder (1016 cm-3) er meget højere end i det uddopede materiale (~1010 cm-3), så ledningsevnen er også mange størrelsesordener højere.
- Aktiveringsenergien for ledning er kun 40-50 meV, så ledningsevnen ændrer sig ikke meget med temperaturen (i modsætning til i den intrinsiske halvleder)
- Minoritetsbærerne (i dette tilfælde huller) bidrager ikke til ledningsevnen, fordi deres koncentration er så meget lavere end majoritetsbærerens (elektroner).
Sådan er ledningsevnen for p-type materialer domineret af huller, og den er også meget højere end den intrinsiske halvleders ledningsevne.
Kemi af halvlederdoping. Nogle gange er det ikke umiddelbart indlysende, hvilken form for doping (n- eller p-type) der induceres ved at “rode” i et halvlederkrystalgitter. Ud over substitution af urenhedsatomer på normale gitterpladser (de eksempler, der er givet ovenfor for Si), er det også muligt at dotere med vacancies – manglende atomer – og med interstitialer – ekstra atomer på pladser, der ikke normalt er besat. Nogle enkle regler er følgende:
- For substitutioner resulterer tilføjelse af et atom til højre i det periodiske system i n-type-doping, og et atom til venstre i p-type-doping.
For eksempel, når TiO2 doteres med Nb på nogle af Ti-siderne eller med F på O-siderne, er resultatet n-type-doping. I begge tilfælde har urenhedsatomet en valenselektron mere end det atom, som det blev erstattet af. Tilsvarende resulterer substitution af en lille mængde Zn i stedet for Ga i GaAs eller en lille mængde Li i stedet for Ni i NiO i p-typen-doping.
- Anionvakancer resulterer i n-typen-doping, og kationvakancer i p-typen-doping.
Eksempler er anionvakancer i CdS1-x og WO3-x, som begge giver n-type halvledere, og kobbervakancer i Cu1-xO, som giver en p-type halvleder.
- Interstitielle kationer (f.eks. Li) donerer elektroner til gitteret, hvilket resulterer i n-type-doping. Interstitielle anioner er ret sjældne, men vil resultere i p-type-doping.
I nogle tilfælde kan der være både p- og n-type-dopingstoffer i samme krystal, f.eks. B- og P-forureninger i et Si-gitter, eller kation- og anionvakancer i et metaloxidgitter. I dette tilfælde kompenserer de to former for dotering hinanden, og doteringstypen bestemmes af den dotering, der er i højere koncentration. Et doteringsstof kan også være til stede på mere end ét sted. F.eks. kan Si være placeret på både Ga- og As-pladserne i GaAs, og de to substitueringer kompenserer hinanden. Si har dog en lille præference for Ga-pladsen, hvilket resulterer i n-type-doping.