Inleiding tot de hyperbolische tangensfunctie
De definitie van de hyperbolische tangensfunctie
De hyperbolische tangensfunctie is een oude wiskundige functie. Zij werd voor het eerst gebruikt in het werk van L’Abbe Sauri (1774).
Deze functie is eenvoudig te definiëren als de verhouding tussen de hyperbolische sinus- en de cosinusfunctie (of uitgebreid, als de verhouding van het halve verschil en de halve som van twee exponentiële functies in de punten ![]() en
en ![]() ):
):
![]()
![]()
Na vergelijking met de beroemde Euler-formules voor de sinus- en cosinusfuncties, ![]() en
en ![]() , is het gemakkelijk om de volgende voorstelling van de hyperbolische tangens af te leiden via de cirkeltangensfunctie:
, is het gemakkelijk om de volgende voorstelling van de hyperbolische tangens af te leiden via de cirkeltangensfunctie:
![]()
![]()
Uit deze formule kunnen alle eigenschappen en formules voor de hyperbolische tangens worden afgeleid uit de overeenkomstige eigenschappen en formules voor de cirkeltangens.
Een snelle blik op de hyperbolische tangensfunctie
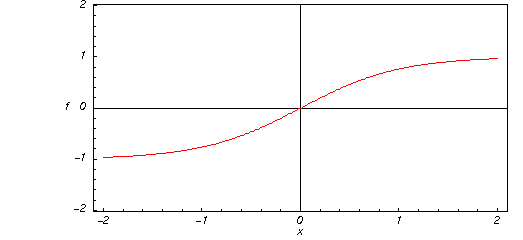
Hier ziet u een grafiek van de hyperbolische tangensfunctie ![]() voor reële waarden van zijn argument
voor reële waarden van zijn argument ![]() .
.
![]()
Voorstelling door meer algemene functies
De hyperbolische tangensfunctie ![]() kan worden voorgesteld met behulp van meer algemene wiskundige functies. Als de verhouding van de hyperbolische sinus- en cosinusfuncties, die bijzondere gevallen zijn van de veralgemeende hypergeometrische, Bessel-, Struve-, en Mathieu-functies, kan de hyperbolische tangensfunctie ook worden voorgesteld als verhoudingen van die bijzondere functies. Maar deze voorstellingen zijn niet erg bruikbaar. Het is nuttiger om de hyperbolische tangensfunctie voor te stellen als bijzondere gevallen van één speciale functie. Dat kan met behulp van dubbelperiodieke Jacobi elliptische functies die ontaarden in de hyperbolische tangensfunctie als hun tweede parameter gelijk is aan
kan worden voorgesteld met behulp van meer algemene wiskundige functies. Als de verhouding van de hyperbolische sinus- en cosinusfuncties, die bijzondere gevallen zijn van de veralgemeende hypergeometrische, Bessel-, Struve-, en Mathieu-functies, kan de hyperbolische tangensfunctie ook worden voorgesteld als verhoudingen van die bijzondere functies. Maar deze voorstellingen zijn niet erg bruikbaar. Het is nuttiger om de hyperbolische tangensfunctie voor te stellen als bijzondere gevallen van één speciale functie. Dat kan met behulp van dubbelperiodieke Jacobi elliptische functies die ontaarden in de hyperbolische tangensfunctie als hun tweede parameter gelijk is aan ![]() of
of ![]() :
:
![]()
![]()
Definitie van de hyperbolische tangensfunctie voor een complex argument
In het complexe ![]() -vlak wordt de functie
-vlak wordt de functie ![]() gedefinieerd door dezelfde formule die voor reële waarden wordt gebruikt:
gedefinieerd door dezelfde formule die voor reële waarden wordt gebruikt:
![]()
![]()
In de punten ![]() , waar
, waar ![]() nulpunten heeft, is de noemer van de laatste formule gelijk aan nul en heeft
nulpunten heeft, is de noemer van de laatste formule gelijk aan nul en heeft ![]() singulariteiten (polen van de eerste orde).
singulariteiten (polen van de eerste orde).
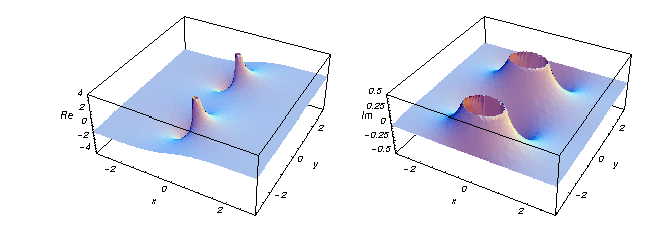
Hier zijn twee grafieken die de reële en imaginaire delen van de hyperbolische tangensfunctie over het complexe vlak tonen.
![]()
De bekendste eigenschappen en formules voor de hyperbolische tangensfunctie
Waarden in punten
De waarden van de hyperbolische tangens voor speciale waarden van zijn argument kunnen eenvoudig worden afgeleid uit overeenkomstige waarden van de cirkeltangens in de speciale punten van de cirkel:
![]()
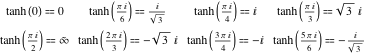
![]()
![]()
![]()
![]()
De waarden op oneindig kunnen worden uitgedrukt met de volgende formules:
![]()
![]()
Algemene eigenschappen
Voor reële waarden van argument ![]() zijn de waarden van
zijn de waarden van ![]() reëel.
reëel.
In de punten ![]() zijn de waarden van
zijn de waarden van ![]() algebraïsch. In verschillende gevallen kunnen ze
algebraïsch. In verschillende gevallen kunnen ze ![]() , 0, of ⅈ zijn:
, 0, of ⅈ zijn:
![]()
![]()
De waarden van ![]() kunnen alleen met vierkantswortels worden uitgedrukt als
kunnen alleen met vierkantswortels worden uitgedrukt als ![]() en
en ![]() een product is van een macht van 2 en verschillende Fermat-priemgetallen {3, 5, 17, 257, …}.
een product is van een macht van 2 en verschillende Fermat-priemgetallen {3, 5, 17, 257, …}.
De functie ![]() is een analytische functie van
is een analytische functie van ![]() die gedefinieerd is over het gehele complexe
die gedefinieerd is over het gehele complexe ![]() -vlak en geen vertakkingen en vertakkingspunten heeft. Zij heeft een oneindige verzameling singuliere punten:
-vlak en geen vertakkingen en vertakkingspunten heeft. Zij heeft een oneindige verzameling singuliere punten:
(a) ![]() zijn de enkelvoudige polen met residuen 1.(b)
zijn de enkelvoudige polen met residuen 1.(b) ![]() is een essentieel singulier punt.
is een essentieel singulier punt.
Het is een periodieke functie met periode ![]() :
:
![]()
![]()
![]()
![]()
De functie ![]() is een oneven functie met spiegelsymmetrie:
is een oneven functie met spiegelsymmetrie:
![]()
![]()
Differentiatie
De eerste afgeleide van ![]() kan eenvoudig worden voorgesteld met behulp van ofwel de functie
kan eenvoudig worden voorgesteld met behulp van ofwel de functie ![]() ofwel de functie
ofwel de functie ![]() :
:
![]()
![]()
De ![]()
![]() afgeleide van
afgeleide van ![]() heeft veel ingewikkelder voorstellingen dan de symbolische
heeft veel ingewikkelder voorstellingen dan de symbolische ![]()
![]() afgeleiden voor
afgeleiden voor ![]() en
en ![]() :
:
![]()
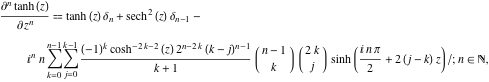
waarbij ![]() het Kronecker-delta-symbool is:
het Kronecker-delta-symbool is: ![]() en
en ![]() .
.
Gewone differentiaalvergelijking
De functie ![]() voldoet aan de volgende eerste-orde niet-lineaire differentiaalvergelijking:
voldoet aan de volgende eerste-orde niet-lineaire differentiaalvergelijking:
![]()
![]()
Reeksvoorstelling
De functie ![]() heeft een eenvoudige reeksexpansie bij de oorsprong die convergeert voor alle eindige waarden
heeft een eenvoudige reeksexpansie bij de oorsprong die convergeert voor alle eindige waarden ![]() met
met ![]() :
:
![]()
![]()
waar ![]() de Bernoulli getallen zijn.
de Bernoulli getallen zijn.
Integrale voorstelling
De functie ![]() heeft een bekende integrale voorstelling door de volgende bepaalde integraal langs het positieve deel van de reële as:
heeft een bekende integrale voorstelling door de volgende bepaalde integraal langs het positieve deel van de reële as:
![]()
![]()
Voortgezette breukvoorstellingen
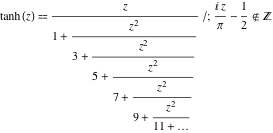
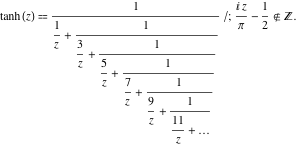
De functie ![]() heeft de volgende eenvoudige voortgezette breukvoorstellingen:
heeft de volgende eenvoudige voortgezette breukvoorstellingen:
![]()
![]()
Oneindige integratie
Oneindige integralen van uitdrukkingen waarbij de hyperbolische tangensfunctie betrokken is, kunnen soms worden uitgedrukt met behulp van elementaire functies. Er zijn echter vaak speciale functies nodig om de resultaten uit te drukken, zelfs als de integranden een eenvoudige vorm hebben (als ze in gesloten vorm kunnen worden geëvalueerd). Hier volgen enkele voorbeelden:
![]()
![]()
![]()
![]()
![]()
![]()
Definitieve integratie
Definiete integralen die de hyperbolische tangensfunctie bevatten zijn soms eenvoudig. De beroemde Catalaanse constante ![]() kan bijvoorbeeld worden gedefinieerd door de volgende integraal:
kan bijvoorbeeld worden gedefinieerd door de volgende integraal:
![]()
![]()
Een aantal speciale functies kan worden gebruikt om ingewikkeldere definitieve integralen te evalueren. De hypergeometrische functie is bijvoorbeeld nodig om de volgende integraal uit te drukken:
![]()
![]()
Eindige sommatie
De volgende eindige som die de hyperbolische tangensfunctie bevat, kan worden uitgedrukt met behulp van hyperbolische cotangensfuncties:
![]()
![]()
Optelformules
De hyperbolische tangens van een som kan worden weergegeven door de regel: “de hyperbolische tangens van een som is gelijk aan de som van de hyperbolische tangens gedeeld door één plus het product van de hyperbolische tangens”. Een soortgelijke regel geldt voor de hyperbolische tangens van het verschil:
![]()
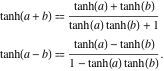
Meervoudige argumenten
In het geval van meervoudige argumenten ![]() ,
, ![]() , …, kan de functie
, …, kan de functie ![]() worden voorgesteld als de verhouding van de eindige sommen die machten van hyperbolische tangens bevatten:
worden voorgesteld als de verhouding van de eindige sommen die machten van hyperbolische tangens bevatten:
![]()
![]()
![]()
![]()
![]()
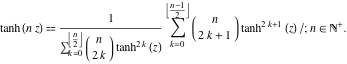
Halve-hoekformules
De hyperbolische tangens van een halve hoek kan met behulp van twee hyperbolische functies worden voorgesteld door de volgende eenvoudige formules:
![]()
![]()
![]()
![]()
De hyperbolische sinusfunctie in de laatste formule kan worden vervangen door de hyperbolische cosinusfunctie. Maar dat leidt tot een ingewikkelder voorstelling die wel geldig is in een horizontale strook:
![]()
![]()
De laatste beperkingen kunnen worden opgeheven door de formule enigszins aan te passen (nu geldt de identiteit voor alle complexe ![]() ):
):
![]()
![]()
Sommen van twee directe functies
De som van twee hyperbolische tangensfuncties kan worden beschreven met de regel: “de som van hyperbolische tangens is gelijk aan de hyperbolische sinus van de som vermenigvuldigd met de hyperbolische secansen”. Een soortgelijke regel geldt voor het verschil van twee hyperbolische tangens:
![]()
![]()
Producten met de directe functie
Het product van twee hyperbolische tangensfuncties en het product van de hyperbolische tangens en de cotangens hebben de volgende voorstellingen:
![]()
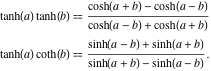
Ongelijkheden
De bekendste ongelijkheid voor de hyperbolische tangensfunctie is de volgende:
![]()
![]()
Relaties met zijn inverse functie
Er zijn eenvoudige relaties tussen de functie ![]() en zijn inverse functie
en zijn inverse functie ![]() :
:
![]()
![]()
![]()
![]()
De tweede formule geldt in ieder geval in de horizontale strook ![]() . Buiten deze strook geldt een veel gecompliceerder verband (dat de eenheidsstap, het reële deel en de bodemfuncties bevat):
. Buiten deze strook geldt een veel gecompliceerder verband (dat de eenheidsstap, het reële deel en de bodemfuncties bevat):
![]()
![]()
Voorstellingen door andere hyperbolische functies
De hyperbolische tangens- en cotangensfuncties worden verbonden door een zeer eenvoudige formule die de lineaire functie in het argument bevat:
![]()
![]()
De hyperbolische tangensfunctie kan ook via andere hyperbolische functies worden voorgesteld door de volgende formules:
![]()
![]()
![]()
![]()
Voorstellingen door goniometrische functies
De hyperbolische tangensfunctie heeft voorstellingen die gebruik maken van de goniometrische functies:
![]()
![]()
![]()
![]()
Toepassingen
De hyperbolische tangensfunctie wordt overal in de wiskunde, de exacte wetenschappen, en de techniek gebruikt.