Introdução à Função Hiperbólica Tangente
Definição da função hiperbólica tangente
A função hiperbólica tangente é uma função matemática antiga. Foi utilizada pela primeira vez no trabalho de L’Abbe Sauri (1774).
Esta função é facilmente definida como a razão entre a função hiperbólica seno e a função cosseno (ou expandida, como a razão da meia-diferença e meia-soma de duas funções exponenciais nos pontos 
e 
):
Após comparação com as famosas fórmulas de Euler para as funções seno e cosseno, 
e 
, é fácil derivar a seguinte representação da tangente hiperbólica através da função tangente circular:
Esta fórmula permite derivar todas as propriedades e fórmulas para a tangente hiperbólica a partir das propriedades e fórmulas correspondentes para a tangente circular.
Uma rápida olhada na função tangente hiperbólica
Aqui está um gráfico da função tangente hiperbólica 
para valores reais do seu argumento 
.
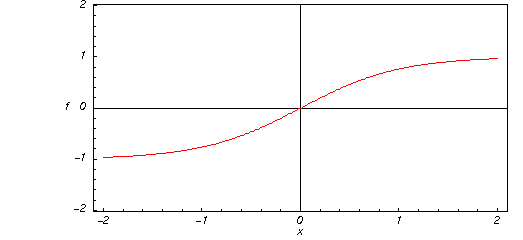
Representação através de funções mais gerais
A função tangente hiperbólica 
pode ser representada usando funções matemáticas mais gerais. Como a razão das funções hiperbólica senoidal e co-seno que são casos particulares das funções hipergeométrica generalizada, Bessel, Struve e Mathieu, a função hiperbólica tangente também pode ser representada como razão dessas funções especiais. Mas estas representações não são muito úteis. É mais útil escrever a função hiperbólica tangente como casos particulares de uma função especial. Isso pode ser feito usando funções elípticas Jacobi duplamente periódicas que degeneram na função tangente hiperbólica quando seu segundo parâmetro é igual a 
ou 
:
Definição da função hiperbólica tangente para um argumento complexo
No complexo 
-plano, a função 
é definida pela mesma fórmula que é usada para valores reais:
> Nos pontos 
, onde 
tem zeros, o denominador da última fórmula é igual a zero e 
tem singularidades (pólos da primeira ordem).
Aqui estão dois gráficos mostrando as partes real e imaginária da função tangente hiperbólica sobre o plano complexo.
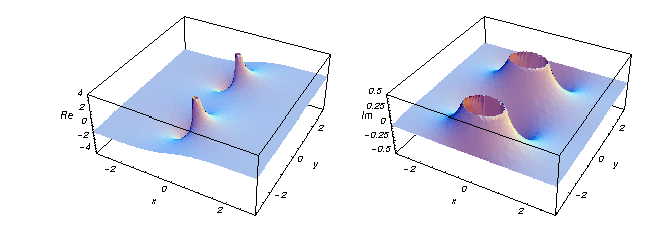
As propriedades e fórmulas mais conhecidas para a função hiperbólica tangente
Valores em pontos
Os valores da tangente hiperbólica para valores especiais do seu argumento podem ser facilmente derivados dos valores correspondentes da tangente circular nos pontos especiais do círculo:
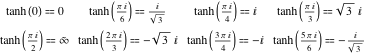
Os valores no infinito podem ser expressos através das seguintes fórmulas
Características gerais
Para valores reais de argumento 
, os valores de 
são reais.
Nos pontos 
, os valores de 
são algébricos. Em vários casos, eles podem ser 
, 0, ou ⅈ:
Os valores de 
só podem ser expressos usando raízes quadradas se 
e 
for um produto de um poder de 2 e primes Fermat distintos {3, 5, 17, 257, …}.
A função 
é uma função analítica de 
que é definida sobre todo o complexo 
-plano e não tem cortes de ramos e pontos de ramos. Tem um conjunto infinito de pontos singulares:
(a) 
são os pólos simples com resíduos 1.(b) 
é um ponto singular essencial.
É uma função periódica com período 
:
A função 
é uma função estranha com simetria de espelho:
Diferenciação
A primeira derivada de 
tem representações simples usando ou a função 
ou a função 
:
A 
derivada de 
tem representações muito mais complicadas que a simbólica 
derivada de 
e 
:
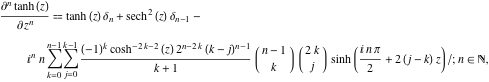
onde 
é o símbolo do delta do Kronecker: 
e 
.
Equação diferencial ordinária
A função 
satisfaz a seguinte equação diferencial não linear de primeira ordem:
Representação em série
A função 
tem uma expansão em série simples na origem que converge para todos os valores finitos 
com 
:
>
onde 
são os números Bernoulli.
Representação integral
A função 
tem uma representação integral bem conhecida através da seguinte integral definida ao longo da parte positiva do eixo real:
Representações de fração contínua
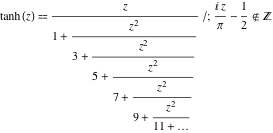
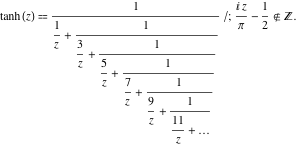
A função 
tem as seguintes representações de fração contínua simples:
Integração indefinida
Integrações indefinidas de expressões envolvendo a função tangente hiperbólica podem às vezes ser expressas usando funções elementares. Entretanto, funções especiais são freqüentemente necessárias para expressar os resultados mesmo quando os integrandos têm uma forma simples (se eles podem ser avaliados de forma fechada). Aqui estão alguns exemplos:
Integração definida
Integrações definidas que contêm a função tangente hiperbólica são às vezes simples. Por exemplo, a famosa constante catalã 
pode ser definida através da seguinte integral:
Algumas funções especiais podem ser usadas para avaliar integrais definidos mais complicados. Por exemplo, a função hipergeométrica é necessária para expressar a seguinte integral:
Soma finita
A seguinte soma finita que contém a função hiperbólica tangente pode ser expressa usando funções hiperbólicas cotangentes:
Fórmulas adicionais
A tangente hiperbólica de uma soma pode ser representada pela regra: “a tangente hiperbólica de uma soma é igual à soma das tangentes hiperbólicas dividida por um mais o produto das tangentes hiperbólicas”. Uma regra semelhante é válida para a tangente hiperbólica da diferença:
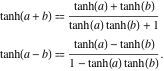
Argumentos múltiplos
No caso de argumentos múltiplos 
, 
, …, a função 
pode ser representada como a razão das somas finitas que inclui as potências das tangentes hiperbólicas:
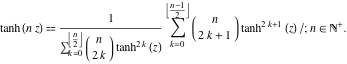
Fórmulas de meio-ângulo
A tangente hiperbólica de um meio-ângulo pode ser representada usando duas funções hiperbólicas através das seguintes fórmulas simples:
A função hiperbólica seno na última fórmula pode ser substituída pela função hiperbólica cosseno. Mas leva a uma representação mais complicada que é válida numa faixa horizontal:
As últimas restrições podem ser removidas modificando ligeiramente a fórmula (agora a identidade é válida para todos os complexos 
):
Soma de duas funções directas
A soma de duas funções hiperbólicas tangentes pode ser descrita pela regra: “a soma das tangentes hiperbólicas é igual ao seno hiperbólico da soma multiplicada pelas secantes hiperbólicas”. Uma regra semelhante é válida para a diferença de duas tangentes hiperbólicas:
Produtos envolvendo a função direta
O produto de duas funções tangentes hiperbólicas e o produto da tangente hiperbólica e cotangente têm as seguintes representações:
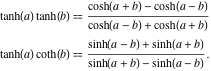
Desigualdades
A desigualdade mais famosa para a função tangente hiperbólica é a seguinte:
Relações com a sua função inversa
Existem relações simples entre a função 
e a sua função inversa 
:
A segunda fórmula é válida pelo menos na faixa horizontal 
. Fora desta tira existe uma relação muito mais complicada (que contém o passo unitário, a parte real e as funções do chão):
Representações através de outras funções hiperbólicas
As funções tangente e cotangente hiperbólicas estão ligadas por uma fórmula muito simples que contém a função linear no argumento:
A função hiperbólica tangente também pode ser representada através de outras funções hiperbólicas através das seguintes fórmulas:
Representações através de funções trigonométricas
A função hiperbólica tangente tem representações que utilizam as funções trigonométricas:
Aplicações
A função hiperbólica tangente é usada em matemática, nas ciências exactas e na engenharia.