Hyperbolischer Tangens: Einführung in die hyperbolische Tangensfunktion

Einführung in die hyperbolische Tangensfunktion

Definition der hyperbolischen Tangensfunktion

Die hyperbolische Tangensfunktion ist eine alte mathematische Funktion. Sie wurde erstmals in der Arbeit von L’Abbe Sauri (1774) verwendet.

Diese Funktion lässt sich leicht als das Verhältnis zwischen der hyperbolischen Sinus- und der Kosinusfunktion definieren (oder erweitert als das Verhältnis von Halbdifferenz und Halbsumme zweier Exponentialfunktionen in den Punkten und ):

Nach dem Vergleich mit den berühmten Eulerschen Formeln für die Sinus- und Kosinusfunktionen, und , ist es leicht, die folgende Darstellung des hyperbolischen Tangens durch die Kreistangentenfunktion herzuleiten:

Diese Formel erlaubt die Ableitung aller Eigenschaften und Formeln für den hyperbolischen Tangens aus den entsprechenden Eigenschaften und Formeln für den Kreistangens.

Ein kurzer Blick auf die hyperbolische Tangensfunktion

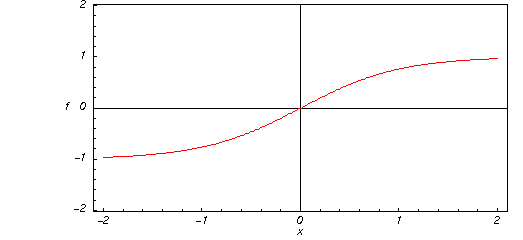
Hier ist eine Grafik der hyperbolischen Tangensfunktion für reelle Werte ihres Arguments .

Darstellung durch allgemeinere Funktionen

Die hyperbolische Tangensfunktion kann durch allgemeinere mathematische Funktionen dargestellt werden. Als Verhältnis der hyperbolischen Sinus- und Kosinusfunktionen, die Spezialfälle der verallgemeinerten hypergeometrischen, Bessel-, Struve- und Mathieu-Funktionen sind, kann die hyperbolische Tangensfunktion auch als Verhältnis dieser Spezialfunktionen dargestellt werden. Diese Darstellungen sind jedoch nicht sehr nützlich. Es ist sinnvoller, die hyperbolische Tangensfunktion als Sonderfälle einer speziellen Funktion darzustellen. Dies kann mit doppelt periodischen elliptischen Jacobi-Funktionen geschehen, die in die hyperbolische Tangensfunktion entarten, wenn ihr zweiter Parameter gleich oder ist:

Definition der hyperbolischen Tangensfunktion für ein komplexes Argument

In der komplexen -Ebene wird die Funktion durch die gleiche Formel definiert, die für reelle Werte verwendet wird:

In den Punkten , wo Nullstellen hat, ist der Nenner der letzten Formel gleich Null und hat Singularitäten (Pole erster Ordnung).

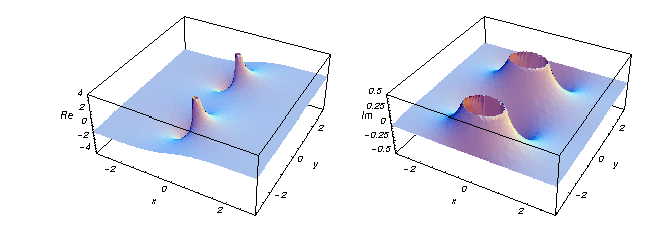
Hier sind zwei Grafiken, die den Real- und Imaginärteil der hyperbolischen Tangensfunktion über der komplexen Ebene zeigen.

Die bekanntesten Eigenschaften und Formeln für die hyperbolische Tangensfunktion

Werte in Punkten

Die Werte des hyperbolischen Tangens für spezielle Werte seines Arguments lassen sich leicht aus entsprechenden Werten des Kreistangens in den speziellen Punkten des Kreises ableiten:

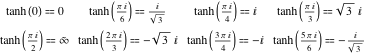
Die Werte im Unendlichen können durch folgende Formeln ausgedrückt werden:

Allgemeine Eigenschaften

Für reelle Werte des Arguments sind die Werte von reell.

In den Punkten sind die Werte von algebraisch. In mehreren Fällen können sie , 0 oder ⅈ sein:

Die Werte von können nur durch Quadratwurzeln ausgedrückt werden, wenn und ein Produkt aus einer Potenz von 2 und verschiedenen Fermat-Primzahlen {3, 5, 17, 257, …} ist.

Die Funktion ist eine analytische Funktion von , die über der gesamten komplexen -Ebene definiert ist und keine Verzweigungsschnitte und Verzweigungspunkte hat. Sie hat eine unendliche Menge von Singulärpunkten:

(a) sind die einfachen Pole mit den Residuen 1.(b) ist ein wesentlicher Singulärpunkt.

Es ist eine periodische Funktion mit Periode :

Die Funktion ist eine ungerade Funktion mit Spiegelsymmetrie:

Differenzierung

Die erste Ableitung von lässt sich entweder durch die Funktion oder die Funktion einfach darstellen:

Die Ableitung von hat viel kompliziertere Darstellungen als die symbolischen Ableitungen für und :

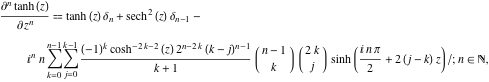
wobei das Kronecker-Deltasymbol ist: und .

Gewöhnliche Differentialgleichung

Die Funktion erfüllt die folgende nichtlineare Differentialgleichung erster Ordnung:

Reihendarstellung

Die Funktion hat eine einfache Reihenentwicklung im Ursprung, die für alle endlichen Werte mit konvergiert:

wobei die Bernoulli-Zahlen sind.

Integraldarstellung

Die Funktion hat eine bekannte Integraldarstellung durch das folgende definite Integral entlang des positiven Teils der reellen Achse:

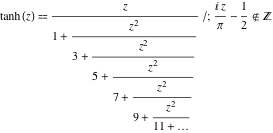
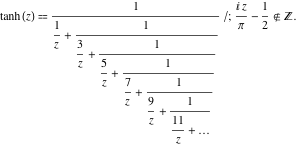
Fortsetzungsbruchdarstellungen

Die Funktion hat die folgenden einfachen Fortsetzungsbruchdarstellungen:

Unbestimmte Integration

Unbestimmte Integrale von Ausdrücken, an denen die hyperbolische Tangensfunktion beteiligt ist, können manchmal durch elementare Funktionen ausgedrückt werden. Häufig werden jedoch spezielle Funktionen benötigt, um die Ergebnisse auszudrücken, auch wenn die Integranden eine einfache Form haben (wenn sie in geschlossener Form ausgewertet werden können). Hier sind einige Beispiele:

Definite Integration

Definite Integrale, die die hyperbolische Tangensfunktion enthalten, sind manchmal einfach. Zum Beispiel kann die berühmte katalanische Konstante durch das folgende Integral definiert werden:

Einige spezielle Funktionen können verwendet werden, um kompliziertere definite Integrale auszuwerten. Zum Beispiel wird die hypergeometrische Funktion benötigt, um das folgende Integral auszudrücken:

Endliche Summation

Die folgende endliche Summe, die die hyperbolische Tangensfunktion enthält, kann durch hyperbolische Kotangensfunktionen ausgedrückt werden:

Additionsformeln

Der hyperbolische Tangens einer Summe lässt sich durch die Regel darstellen: „Der hyperbolische Tangens einer Summe ist gleich der Summe der hyperbolischen Tangens geteilt durch eins plus dem Produkt der hyperbolischen Tangens“. Eine ähnliche Regel gilt für den hyperbolischen Tangens der Differenz:

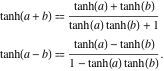
Mehrere Argumente

Im Falle mehrerer Argumente , , …, kann die Funktion als Verhältnis der endlichen Summen dargestellt werden, das Potenzen von hyperbolischen Tangenten einschließt:

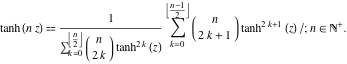
Halbwinkelformeln

Der hyperbolische Tangens eines Halbwinkels lässt sich mit zwei hyperbolischen Funktionen durch folgende einfache Formeln darstellen:

Die hyperbolische Sinusfunktion in der letzten Formel kann durch die hyperbolische Kosinusfunktion ersetzt werden. Dies führt jedoch zu einer komplizierteren Darstellung, die in einem horizontalen Streifen gültig ist:

Die letzten Einschränkungen können durch eine leichte Modifikation der Formel aufgehoben werden (jetzt gilt die Identität für alle komplexen ):

Summen zweier direkter Funktionen

Die Summe zweier hyperbolischer Tangensfunktionen kann durch die Regel beschrieben werden: „Die Summe der hyperbolischen Tangens ist gleich dem hyperbolischen Sinus der Summe multipliziert mit den hyperbolischen Sekanten“. Eine ähnliche Regel gilt für die Differenz zweier hyperbolischer Tangenten:

Produkte mit der direkten Funktion

Das Produkt zweier hyperbolischer Tangensfunktionen und das Produkt von hyperbolischem Tangens und Kotangens haben folgende Darstellungen:

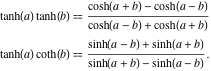
Ungleichungen

Die bekannteste Ungleichung für die hyperbolische Tangensfunktion ist die folgende:

Beziehungen zu ihrer Umkehrfunktion

Es gibt einfache Beziehungen zwischen der Funktion und ihrer Umkehrfunktion :

Die zweite Formel ist zumindest im horizontalen Streifen gültig. Außerhalb dieses Streifens gilt eine viel kompliziertere Beziehung (die den Einheitsschritt, den Realteil und die Bodenfunktionen enthält):