När data är redo att analyseras bör det grundligt bedömas, baserat på en inspektion av data, om statistiska metoder bör användas för att hantera saknade data. Bell et al. syftade till att bedöma omfattningen och hanteringen av saknade data i randomiserade kliniska prövningar som publicerades mellan juli och december 2013 i BMJ, JAMA, Lancet och New England Journal of Medicine . 95 % av de 77 identifierade prövningarna rapporterade några saknade resultatuppgifter. Den vanligaste metoden för att hantera saknade data i den primära analysen var fullständig fallanalys (45 %), enkel imputering (27 %), modellbaserade metoder (t.ex. blandade modeller eller generaliserade estimerande ekvationer) (19 %) och multipel imputering (8 %) .
Fullständig fallanalys
Fullständig fallanalys är en statistisk analys som baseras på deltagare med en fullständig uppsättning utfallsdata. Deltagare som saknar uppgifter utesluts från analysen. Som beskrivs i inledningen, om de saknade uppgifterna är MCAR kommer den fullständiga fallanalysen att ha en minskad statistisk styrka på grund av den minskade urvalsstorleken, men de observerade uppgifterna kommer inte att vara snedvridna . Om de saknade uppgifterna inte är MCAR kan den fullständiga analysens uppskattning av interventionseffekten vara baserad, dvs. det kommer ofta att finnas en risk för överskattning av nyttan och underskattning av skadan . Se avsnittet ”Bör multipel imputering användas för att hantera saknade uppgifter?” för en mer detaljerad diskussion om den potentiella giltigheten om fullständig fallanalys tillämpas.
Enskild imputering
När man använder enskild imputering ersätts saknade värden med ett värde som definieras av en viss regel . Det finns många former av singelimputering, t.ex. sista observation som överförs (en deltagares saknade värden ersätts med deltagarens senast observerade värde), värsta observation som överförs (en deltagares saknade värden ersätts med deltagarens värsta observerade värde) och enkel medelvärdesimputering . Vid enkel medelvärdesimputering ersätts de saknade värdena med medelvärdet för den variabeln . Användning av enkel imputering resulterar ofta i en underskattning av variabiliteten eftersom varje icke-observerat värde har samma vikt i analysen som de kända, observerade värdena . Giltigheten av enkel imputering beror inte på om uppgifterna är MCAR eller inte; enkel imputering beror snarare på särskilda antaganden om att de saknade värdena t.ex. är identiska med det senast observerade värdet . Dessa antaganden är ofta orealistiska och enkel imputering är därför ofta en potentiellt snedvriden metod och bör användas med stor försiktighet .
Multipel imputering
Multipel imputering har visat sig vara en giltig allmän metod för att hantera saknade uppgifter i randomiserade kliniska prövningar, och denna metod är tillgänglig för de flesta typer av uppgifter . Vi kommer i följande avsnitt att beskriva när och hur multipel imputering bör användas.
Bör multipel imputering användas för att hantera saknade data?
Rsaker till varför multipel imputering inte bör användas för att hantera saknade data
Är det giltigt att bortse från saknade data?
Analys av observerade data (complete case analysis) där man bortser från saknade data är en giltig lösning under tre omständigheter.
- a)
En fullständig fallanalys kan användas som den primära analysen om andelen saknade uppgifter är under cirka 5 % (som en tumregel) och det är osannolikt att vissa patientgrupper (t.ex. de mycket sjuka eller de mycket ”välmående” deltagarna) specifikt går förlorade i uppföljning i en av de jämförda grupperna . Med andra ord, om den potentiella effekten av de saknade uppgifterna är försumbar kan de saknade uppgifterna ignoreras i analysen . Känslighetsanalyser för bästa och sämsta fall kan användas i tveksamma fall: först genereras ett dataset för ”bästa och sämsta fall” där det antas att alla deltagare som gått förlorade i uppföljningen i den ena gruppen (kallad grupp 1) har haft ett gynnsamt utfall (t.ex. inte haft någon allvarlig negativ händelse), och att alla deltagare med saknade resultat i den andra gruppen (grupp 2) har haft ett skadligt utfall (t.ex. en allvarlig negativ händelse) . Därefter genereras ett dataset för det ”värsta bästa scenariot” där det antas att alla deltagare som förlorats i uppföljningen i grupp 1 har haft ett skadligt utfall och att alla deltagare som förlorats i uppföljningen i grupp 2 har haft ett gynnsamt utfall . Om kontinuerliga resultat används kan ett ”gynnsamt resultat” vara gruppens medelvärde plus 2 standardavvikelser (eller 1 standardavvikelse) av gruppens medelvärde, och ett ”skadligt resultat” kan vara gruppens medelvärde minus 2 standardavvikelser (eller 1 standardavvikelse) av gruppens medelvärde . För dikotomiserade data kommer dessa känslighetsanalyser för bästa och sämsta fall att visa osäkerhetsintervallet på grund av saknade data, och om detta intervall inte ger kvalitativt motsägelsefulla resultat kan man bortse från de saknade uppgifterna. För kontinuerliga data kommer imputering med 2 SD att representera ett möjligt osäkerhetsintervall givet 95 % av de observerade data (om de är normalfördelade).
- b)
Om det bara är den beroende variabeln som har saknade värden och hjälpvariablerna (variabler som inte ingår i regressionsanalysen, men som är korrelerade med en variabel som har saknade värden och/eller är relaterade till att den är saknad) inte identifieras, kan en fullständig analys av fall användas som den primära analysen och inga särskilda metoder bör användas för att hantera saknade data. Ingen ytterligare information kommer att erhållas genom att till exempel använda multipel imputering, men standardfelen kan öka på grund av den osäkerhet som införs genom multipel imputering .
- c)
Som nämnts ovan (se Metoder för att hantera saknade uppgifter), skulle det också vara giltigt att bara utföra en fullständig fallanalys om det är relativt säkert att uppgifterna är MCAR (se Inledning). Det är relativt sällan som det är säkert att uppgifterna är MCAR. Det är möjligt att testa hypotesen att uppgifterna är MCAR med Littles test , men det kan vara oklokt att bygga vidare på tester som visade sig vara insignifikanta. Om det därför finns rimliga tvivel om huruvida data är MCAR, även om Littles test är insignifikant (misslyckas med att förkasta nollhypotesen att data är MCAR), bör MCAR inte antas.
Är andelen saknade data för stor?
Om stora andelar data saknas bör det övervägas att bara redovisa resultaten av den kompletta fallanalysen och sedan tydligt diskutera de tolkningsmässiga begränsningarna av försöksresultaten som följer därav. Om flera imputeringar eller andra metoder används för att hantera saknade uppgifter kan det tyda på att försöksresultaten är bekräftande, vilket de inte är om det saknas många uppgifter. Om andelen saknade uppgifter är mycket stor (t.ex. mer än 40 %) för viktiga variabler kan försöksresultaten endast betraktas som hypotesgenererande resultat . Ett sällsynt undantag är om den underliggande mekanismen bakom de saknade uppgifterna kan beskrivas som MCAR (se stycket ovan).
Var både MCAR- och MAR-antagandet osannolika?
Om MAR-antagandet verkar osannolikt på grund av egenskaperna hos de saknade uppgifterna riskerar försöksresultaten att bli snedvridna på grund av ”ofullständiga utfallsdata”, och ingen statistisk metod kan med säkerhet ta hänsyn till denna potentiella snedvridning . Validiteten hos de metoder som används för att hantera MNAR-data kräver vissa antaganden som inte kan testas utifrån observerade data. Känslighetsanalyser av bästa och sämsta fall kan visa hela det teoretiska osäkerhetsintervallet, och slutsatserna bör relateras till detta osäkerhetsintervall. Analysernas begränsningar bör diskuteras och beaktas grundligt.
Är utfallsvariabeln med saknade värden kontinuerlig och är den analytiska modellen komplicerad (t.ex. med interaktioner)?
I denna situation kan man överväga att använda den direkta maximala sannolikhetsmetoden för att undvika problem med modellkompatibilitet mellan den analytiska modellen och modellen för multipel imputering, där den förstnämnda modellen är mer generell än den senare. I allmänhet kan direkta maximum likelihood-metoder användas, men såvitt vi vet är kommersiellt tillgängliga metoder för närvarande endast tillgängliga för kontinuerliga variabler.
När och hur man använder multipel imputering
Om ingen av ”Anledningar till varför multipel imputering inte bör användas för att hantera saknade uppgifter” från ovan är uppfylld, så kan multipel imputering användas. Olika förfaranden har föreslagits i litteraturen under de senaste decennierna för att hantera saknade uppgifter . Vi har beskrivit de ovan nämnda övervägandena av statistiska metoder för att hantera saknade uppgifter i figur 1.
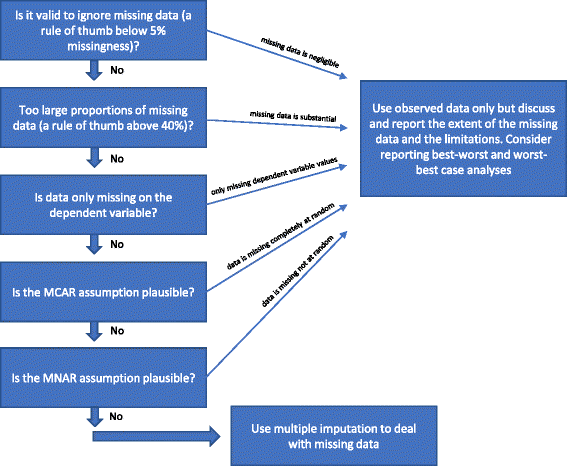
Flödesschema: När bör multipel imputering användas för att hantera saknade data vid analys av resultat av randomiserade kliniska prövningar
Multipel imputering har sitt ursprung i början av 1970-talet, och har vunnit allt större popularitet under åren . Multipel imputering är en simuleringsbaserad statistisk teknik för att hantera saknade uppgifter . Multipel imputering består av tre steg:
-
Imputeringssteg. En ”imputering” representerar i allmänhet en uppsättning plausibla värden för saknade uppgifter – multipel imputering representerar flera uppsättningar plausibla värden . Vid användning av multipel imputering identifieras saknade värden och ersätts med ett slumpmässigt urval av imputeringar med rimliga värden (kompletta dataset). Flera fullständiga datamängder genereras med hjälp av en vald modell för imputering . Fem imputerade dataset har traditionellt föreslagits vara tillräckliga på teoretiska grunder, men 50 dataset (eller fler) verkar vara att föredra för att minska urvalets variabilitet från imputeringsprocessen .
-
Steget för analys av fullständiga data (skattning). Den önskade analysen utförs separat för varje dataset som genereras under imputeringssteget . Härigenom konstrueras till exempel 50 analysresultat.
-
Skede för poolning. De resultat som erhålls från varje avslutad dataanalys kombineras till ett enda resultat av flera imputeringar . Det finns inget behov av att genomföra en viktad metaanalys eftersom alla nämnda 50 analysresultat anses ha samma statistiska vikt.
Det är av stor vikt att det antingen finns kompatibilitet mellan imputeringsmodellen och analysmodellen eller att imputeringsmodellen är mer generell än analysmodellen (t.ex. att imputeringsmodellen innehåller fler oberoende kovariater än analysmodellen) . Om analysmodellen till exempel har betydande interaktioner bör imputeringsmodellen också inkludera dem , om analysmodellen använder en transformerad version av en variabel bör imputeringsmodellen använda samma transformering osv.
Differenta typer av multipel imputering
Det finns olika typer av metoder för multipel imputering. Vi kommer att presentera dem i enlighet med deras ökande grad av komplexitet: 1) regressionsanalys med ett enda värde, 2) monoton imputering, 3) kedjeekvationer eller Markov Chain Monte Carlo-metoden (MCMC). Vi kommer i följande punkter att beskriva dessa olika metoder för multipel imputering och hur man väljer mellan dem.
En regressionsanalys med en enda variabel omfattar en beroende variabel och de stratifieringsvariabler som används vid randomiseringen. Stratifieringsvariablerna omfattar ofta en centrumindikator om studien är en multicenterstudie och vanligtvis en eller flera justeringsvariabler med prognostisk information som är korrelerade med utfallet. Om man använder en kontinuerlig beroende variabel kan ett baslinjevärde för den beroende variabeln också ingå. Såsom nämns i ”Skäl till varför statistiska metoder inte bör användas för att hantera saknade uppgifter” bör en fullständig fallanalys utföras om endast den beroende variabeln har saknade värden och hjälpvariabler inte har identifierats, och inga särskilda metoder bör användas för att hantera de saknade uppgifterna . Om hjälpvariabler har identifierats kan en imputering av en enda variabel utföras. Om det finns betydande brister i baslinjevariabeln för en kontinuerlig variabel kan en fullständig fallanalys ge snedvridna resultat . Därför utförs alltid en imputering av en enda variabel (med eller utan hjälpvariabler som inkluderas i förekommande fall) om endast baslinjevariabeln saknas.
Om både den beroende variabeln och baslinjevariabeln saknas och om det är monotont att variabeln saknas, görs en monoton imputering. Anta en datamatris där patienterna representeras av rader och variablerna av kolumner. Bristen på information i en sådan datamatris sägs vara monoton om kolumnerna kan ordnas så att för varje patient a) om ett värde saknas, saknas alla värden till höger om dess position också saknas, och b) om ett värde observeras, observeras alla värden till vänster om detta värde också. Om det saknas värden är monotont är metoden för multipel imputering också relativt okomplicerad, även om mer än en variabel har saknade värden . I detta fall är det relativt enkelt att imputera de saknade uppgifterna med hjälp av sekventiell regressionsimputering där de saknade värdena imputeras för varje variabel i taget . Många statistikpaket (t.ex. STATA) kan analysera om den saknade variabeln är monoton eller inte.
Om den saknade variabeln inte är monoton genomförs en multipel imputering med hjälp av kedjeekvationer eller MCMC-metoden. Hjälpvariabler inkluderas i modellen om de finns tillgängliga. Vi har sammanfattat hur man väljer mellan de olika metoderna för multipel imputering i figur 2.
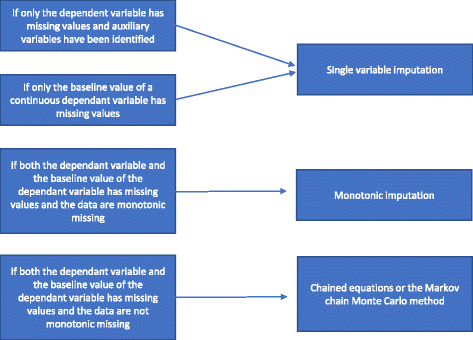
Flödesschema över multipel imputering
Full information maximum likelihood
Full information maximum likelihood är en alternativ metod för att hantera saknade data . Principen för skattning med maximal sannolikhet är att skatta parametrar för den gemensamma fördelningen av utfallet (Y) och kovariater (X1,…, Xk) som, om de vore sanna, skulle maximera sannolikheten för att observera de värden som vi faktiskt har observerat . Om värden saknas för en viss patient kan vi få fram sannolikheten genom att summera den vanliga sannolikheten över alla möjliga värden för de saknade uppgifterna, förutsatt att mekanismen för saknade uppgifter inte kan ignoreras. Denna metod kallas full information maximum likelihood .
Full information maximum likelihood har både styrkor och begränsningar jämfört med multipel imputering.
Styrkor med full information maximum likelihood jämfört med multipel imputering
- 1)
Det är enklare att genomföra, dvs. Det är inte nödvändigt att gå igenom olika steg som vid användning av multipel imputering.
- 2)
Till skillnad från multipel imputering har full information maximum likelihood inga potentiella problem med inkompatibilitet mellan imputeringsmodellen och analysmodellen (se ”Multipel imputering”). Giltigheten av resultaten av multipel imputering kommer att ifrågasättas om det finns en inkompatibilitet mellan imputeringsmodellen och analysmodellen, eller om imputeringsmodellen är mindre generell än analysmodellen .
- 3)
Vid användning av multipel imputering ersätts alla saknade värden i varje genererat dataset (imputeringssteg) med ett slumpmässigt urval av troliga värden . Om inte ”ett slumpmässigt frö” anges kommer därför olika resultat att visas varje gång en multipel imputeringsanalys utförs . Analyser där man använder full information maximum likelihood på samma datamängd kommer att ge samma resultat varje gång analysen utförs, och resultaten är därför inte beroende av ett slumpmässigt tal. Om det slumpmässiga frövärdet definieras i den statistiska analysplanen kan detta problem dock lösas.
Begränsningar av full information maximum likelihood jämfört med multipel imputering
Begränsningarna av att använda full information maximum likelihood jämfört med att använda multipel imputering, är att det endast är möjligt att använda full information maximum likelihood med hjälp av en speciellt utformad programvara . Det har utvecklats preliminära programvaror, men de flesta av dessa saknar de funktioner som finns i kommersiellt utformade statistiska programvaror (t.ex. STATA, SAS eller SPSS). I STATA (med kommandot SEM) och SAS (med kommandot PROC CALIS) är det möjligt att använda maximal sannolikhet med fullständig information, men endast när man använder kontinuerliga beroende variabler (resultatvariabler). För logistisk regression och Cox-regression är det enda kommersiella paketet som ger full information maximum likelihood för saknade data Mplus.
En annan potentiell begränsning när man använder full information maximum likelihood är att det kan finnas ett underliggande antagande om multivariat normalitet . Trots detta kan överträdelser av antagandet om multivariat normalitet inte vara så viktiga, så det kan vara acceptabelt att inkludera binära oberoende variabler i analysen.
Vi har i Additional file 1 inkluderat ett program (SAS) som producerar ett fullständigt leksaksdataset med flera olika analyser av dessa data. Tabell 1 och tabell 2 visar resultatet och hur olika metoder som hanterar saknade data ger olika resultat.
Panelvärden regressionsanalys
Paneldata finns vanligen i en så kallad bred datafil där den första raden innehåller variabelnamnen och efterföljande rader (en för varje patient) innehåller motsvarande värden. Utfallet representeras av olika variabler – en för varje planerad, tidsbestämd mätning av utfallet. För att analysera uppgifterna måste man omvandla filen till en så kallad lång fil med en post per planerad mätning av utfallet, inklusive utfallsvärdet, tidpunkten för mätningen och en kopia av alla andra variabelvärden utom dem för utfallsvariabeln. För att bibehålla korrelationerna inom patienten mellan de tidsbestämda utfallsmåtten är det vanlig praxis att utföra en multipelimputering av datafilen i dess breda form följt av en analys av den resulterande filen efter det att den har konverterats till dess långa form. Proc mixed (SAS 9.4) kan användas för analys av kontinuerliga resultatvärden och proc. glimmix (SAS 9.4) för andra typer av resultat. Eftersom dessa förfaranden tillämpar den direkta maximala sannolikhetsmetoden på utfallsdata, men ignorerar fall med saknade kovariantvärden, kan förfarandena användas direkt när endast värden för beroende variabler saknas och inga bra hjälpvariabler finns tillgängliga. I annat fall bör proc. mixed eller proc. glimmix (beroende på vad som är lämpligt) användas efter en multipel beräkning. Det är uppenbart att ett motsvarande tillvägagångssätt kan vara möjligt med hjälp av andra statistikpaket.
Känslighetsanalyser
Känslighetsanalyser kan definieras som en uppsättning analyser där data hanteras på ett annat sätt jämfört med den primära analysen. Känslighetsanalyser kan visa hur andra antaganden än de som gjorts i den primära analysen påverkar de erhållna resultaten . Känslighetsanalyser bör definieras och beskrivas i förväg i den statistiska analysplanen, men ytterligare känslighetsanalyser i efterhand kan vara motiverade och giltiga. När den potentiella påverkan av saknade värden är oklar rekommenderar vi följande känslighetsanalyser:
-
Vi har redan beskrivit användningen av känslighetsanalyser för bästa värsta och värsta bästa fall för att visa osäkerhetsintervallet på grund av saknade uppgifter (se Bedömning av om metoder bör användas för att hantera saknade uppgifter). Vår tidigare beskrivning av känslighetsanalyser för bästa värsta och sämsta fall gällde saknade uppgifter om antingen en dikotom eller en kontinuerlig beroende variabel, men dessa känslighetsanalyser kan också användas när uppgifter saknas om stratifieringsvariabler, baslinjevärden osv. Den potentiella påverkan av saknade uppgifter bör bedömas för varje variabel separat, dvs. det bör finnas ett bästa värsta och ett sämsta scenario för varje variabel (beroende variabel, utfallsindikatorn och stratifieringsvariablerna) med saknade uppgifter.
-
Om det beslutas att t.ex. multipla imputationer ska användas bör dessa resultat vara det primära resultatet av det givna utfallet. Varje primär regressionsanalys bör alltid kompletteras med en motsvarande analys av observerade (eller tillgängliga) fall.
När metoder med blandade effekter används
Användning av en multicenterförsöksdesign kommer ofta att vara nödvändig för att rekrytera ett tillräckligt antal försöksdeltagare inom en rimlig tidsram . En multicenterstudie ger också en bättre grund för en senare generalisering av resultaten . Det har visat sig att de vanligaste analysmetoderna i randomiserade kliniska prövningar fungerar bra med ett litet antal centra (analys av binära beroende resultat) . Med ett relativt stort antal centra (50 eller fler) är det ofta optimalt att använda ”centrum” som en slumpmässig effekt och att använda analysmetoder med blandade effekter. Det är ofta också lämpligt att använda analysmetoder med blandade effekter vid analys av longitudinella data . Under vissa omständigheter kan det vara lämpligt att inkludera kovariatet med ”slumpmässig effekt” (t.ex. ”centrum”) som en kovariat med fast effekt under imputeringssteget och sedan använda analys med blandade modeller eller generaliserade skattningsekvationer (GEE) under analyssteget . Tillämpningen av en modell med blandade effekter (med t.ex. ”centrum” som en slumpmässig effekt) innebär dock att man måste ta hänsyn till uppgifternas flerskiktade struktur när man modellerar den multipla imputeringen. Nu finns det ingen kommersiell programvara som är direkt tillgänglig för att göra detta. Man kan dock använda REALCOME-paketet som kan kopplas till STATA . Gränssnittet exporterar data med saknade värden från STATA till REALCOM där imputeringen görs med hänsyn till datans flernivåstruktur och med hjälp av en MCMC-metod som omfattar kontinuerliga variabler och som genom att använda en latent normalmodell också möjliggör en korrekt hantering av diskreta data. De imputerade datamängderna kan sedan analyseras med hjälp av STATA-kommandot ”mi estimate:” som kan kombineras med ”mixed” (för ett kontinuerligt utfall) eller ”meqrlogit” för binära eller ordinala utfall i STATA . Vid analys av paneldata kan man dock lätt hamna i en situation där data omfattar tre eller fler nivåer, t.ex. mätningar inom samma patient (nivå-1), patienter inom centra (nivå-2) och centra (nivå-3) . För att inte ge oss in på en ganska komplicerad modell som kan leda till bristande konvergens eller instabila standardfel och som det inte finns någon kommersiell programvara för, rekommenderar vi att man antingen behandlar centrumeffekten som fast (direkt eller efter sammanslagningen av små centra till ett eller flera centra av lämplig storlek med hjälp av ett förfarande som måste föreskrivas i planen för den statistiska analysen) eller att man utesluter centrum som en kovariabel. Om randomiseringen har stratifierats efter centrum kommer det senare tillvägagångssättet att leda till en uppåtgående bias i standardfelen, vilket resulterar i ett något konservativt testförfarande .
.