Lotka-Volterra ekvationerna beskriver en ekologisk rovdjurs- och bytesmodell (eller parasit- och värddjursmodell) där man antar att, för en uppsättning fasta positiva konstanter 
(bytesdjurens tillväxthastighet), 
(den hastighet med vilken rovdjur förstör bytesdjur), 
(rovdjurens dödshastighet) och 
(den hastighet med vilken rovdjur ökar genom att konsumera bytesdjur), följande villkor gäller.
1. En bytespopulation 
ökar med en hastighet 
(proportionell mot antalet bytesdjur) men förstörs samtidigt av rovdjur med en hastighet 
(proportionell mot produkten av antalet bytesdjur och rovdjur).
2. En rovdjurspopulation 
minskar med en hastighet 
(proportionellt mot antalet rovdjur), men ökar med en hastighet 
(återigen proportionellt mot produkten av antalet bytesdjur och rovdjur).
Detta ger de kopplade differentialekvationerna
 |
 |
 |
(1)
|
 |
 |
 |
(2)
|
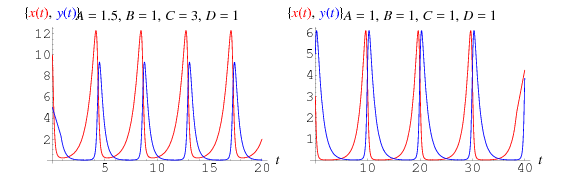
lösningar som visas ovan, där byten visas i rött och rovdjur i blått. I den här typen av modell leder byteskurvan alltid rovdjurskurvan.
Kritiska punkter uppstår när 
, så
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
Den enda stationära punkten ligger alltså vid 
.