Introduktion
På denna sida går vi igenom kontinuitetsekvationen, som tvingar fram bevarandet av massan i en eulersk analys. Detta är inte i egentlig mening en beskrivning av materialbeteende, men den resulterande ekvationen används ofta som en identitet som toalgebraiskt manipulerar konstitutiva modeller som beskriver materialbeteende. Det är alltså värt att se över den. Den är också central för analysen av vätskeflöden eftersom klassiska vätskeanalyser inte kan vara lagrangska eftersom positionerna för alla vätskepartiklar vid \(t = 0\) är okända.
Massakonservering
Kontinuitetsekvationen återspeglar det faktum att massan är bevarad i alla icke-nukleära kontinuummekaniska analyser. Ekvationen utvecklas genom att man adderar den hastighet med vilken massan flödar in och ut ur en kontrollvolym och ställer in nettoflödet lika med förändringshastigheten för massan i volymen. Detta visas i figuren nedan.
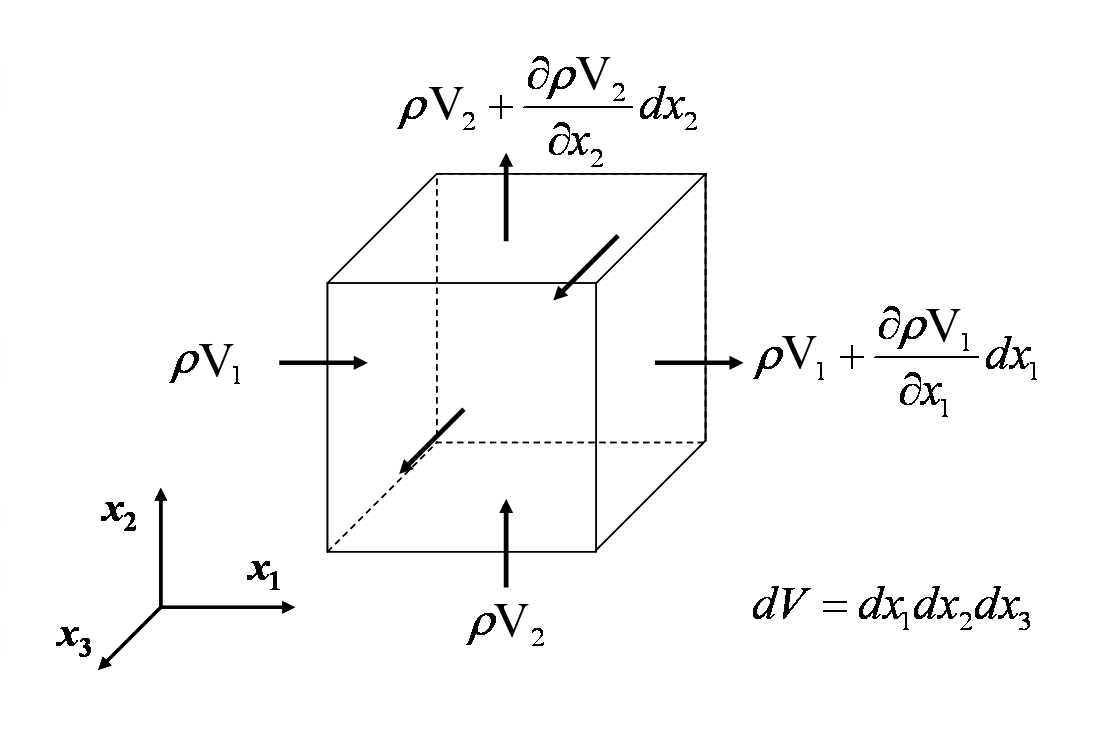
Genom att jämföra alla massflöden in i och ut ur den differentiella kontrollvolymen får man
\
\
Kan man stryka termerna och dividera med \(dx_1 dx_2 dx_3\) ger
\
och omarrangemang ger
\
Detta kan skrivas kortfattat som
\

Väsentliga punkter
Detta är de sista, fullständiga och mest allmänna formerna av den kontinuerliga ekvation som upprätthåller massans bevarande. Den gäller för alla material, inte bara vätskor. Den gäller alltså även för fasta ämnen. Observera att det är en enda skalär ekvation och att den är eulersk till sin natur eftersom gradienttermerna är \({\partial \over \partial x_i}\), inte \({\partial \over \partial X_i}\).
Man kan undra om det finns en lagrangisk motsvarighet till den eulerska formen av detta. Det finns det. Den brukar skrivas som
\
Detta säger helt enkelt att den differentiella massan i det deformerade tillståndet\(\rho \, dV\) måste vara lika med sitt ursprungliga värde\(\rho_o dV_o\) i det odeformerade tillståndet.
Det finns flera specialfall av kontinuitetsekvationen.Det första inträffar när flödet är steady state. I detta fall är derivatan med avseende på tiden noll, vilket ger.
\
Det andra specialfallet är inkompressibilitet, dvs, \(\rho = \)konstant.I detta fall är den tidsmässiga derivatan noll och \(\rho\) kan räknas bort från ekvationen så att endast
Detta resultat är så enkelt att det ofta utvidgas.
Notera att detta inte är något annat än \(\text{tr}({\bf D}) = 0\) för fallet med inkompressiva material.

Materialderivat
Följande är värt att påpeka eftersom det tillåter att täthets- och hastighetsvektorn separeras. Det första steget är att tillämpa produktregeln på divergenstermen i kontinuitetsekvationen.
\
Och notera sedan att\({\partial \rho \over \partial t} + {\bf v} \cdot \nabla \rho\)bara är den materiella derivatan av densiteten,\({D \rho \over D t}\).
Så kontinuitetsekvationen kan också skrivas som
\
Om materialet är inkompressibelt kan \(\rho\) inte ändras, så\( {D \rho \over D t} \) måste vara noll, vilket ger
\
Och sedan dividerar man genom med \(\rho\) (eftersom den inte är noll) för att få
\

Kontinuitetsjämförelse Exempel
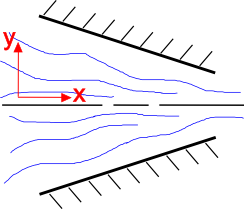
Det är intuitivt att flödet av en vätska ökar i hastighet när tvärsnittsarean minskar, som det visas till höger. Kontinuitetsekvationen förklarar detta. Betrakta ett 2-dimensionellt, stationärt flödesfält av en inkompressibel vätska. kontinuitetsekvationen för denna situation är
\
Start med att titta på y-komponenten av flödet, \(v_2\). Geometrin hos det konvergerande munstycket tvingar \(v_2\) komponenten att strömma uppåt när \(y \lt 0\) och nedåt när \(y \gt 0\). Så \(v_2 \gt 0\) när\(y \lt 0\) och \(v_2 \lt 0\) när \(y \gt 0\).
Nettoeffekten av detta är att \({\partial v_2 \over \partial x_2} \lt 0\)i det konvergerande munstycket.
Men kontinuitetsekvationen föreskriver att summan av de två partiella derivatorerna måste vara lika med noll. Så om den andra är mindre än noll,då
\
och det betyder att vätskeflödet måste accelerera.