Konkav vs konvex?

Vad är skillnaden mellan konkav och konvex?

Om vi skulle beskriva skillnaden mellan konkav och konvex på ett så generellt sätt som möjligt skulle vi säga att alla ihåliga, skålliknande föremål är konkava, medan alla föremål som påminner om en rugbyboll eller en fotboll har en konvex form. Men kanske beror anledningen till att konvex och konkav så ofta missbrukas på att de två orden inte är så enkla som vi skulle vilja att de var.

De flesta grammatikkällor insisterar på hur det är möjligt att använda mnemoteknik för att dechiffrera konvex och konkav genom ordgrottan. Medan föreställningen om att associera konkav med händelsen att något ”grottar in” hjälper till att lära sig om ytegenskaper, är det förvirrande att relatera denna idé till ämnen som involverar grafer.

För att förstå hur konkava och konvexa skiljer sig från varandra, måste vi lära oss hur varje term används i egenskapen av matematik, speglar, linser, och slutligen inom kreativt skrivande. När du väl har bestämt dig för vilket sammanhang du vill använda ord som konkav och konvex, kan du genom att lära dig om deras tekniska aspekter bli mer säker på att använda dem i vardagligt tal.

Vad betyder konkav?

Konkav används som adjektiv eller substantiv för att beskriva formen på ett föremål eller en yta som är böjd inåt eller urholkad som en skål. Exempel på konkav i en mening är bland annat:

”Hon skrapade glass från behållaren och lämnade ett konkavt fotavtryck.”

Enligt The Oxford Dictionary of Word Histories härstammar ordet konkav från sen medelengelska. Konkav och konkavitet återger den latinska termen concavus (con- och cavus), som kan översättas till ”tillsammans” och ”ihåligt” (”Concave”, 110).

Synonymer till konkav är bland annat:

Denka, nedtryckt, skålad, ihålig, intryckt, fördjupad och nedsänkt.

Antonymer av konkav är bland annat:

Bullig, kammarformad, utskjutande, utskjutande, utskjutande, utskjutande.

Vad betyder konvex?

Ordet konvex, eller konvexitet, är ett adjektiv som beskriver ett föremål eller en yta som är rundad eller krökt. När det gäller föremål är mittytan på ett konvext föremål bredare än dess yttre hörn. Exempel på konvex i en mening är bland annat följande,

”Jag föll i giftig murgröna och har nu röda, konvexa knölar över hela huden”.

Synonymer till konvex är bland annat:

Böjd, böjd, utbuktande, upphöjd.

Antonymer av konvex är bland annat:

Den är nedtryckt, sjunkande.

Konkava vs konvexa funktioner

En konvex funktion representerar en kontinuerlig linje på en graf där mittpunkten, eller medianhelheten i ett område, inte överstiger intervallets medelvärde. En konkav funktion är raka motsatsen till en konvex funktion eftersom, för att f(x) ska vara konkav måste f(x) vara negativ. För att göra skillnaderna tydligare följer här en snabb genomgång av hur termerna förhåller sig till varandra:

Konkav uppåt = konvex = konvex nedåt

Konkav nedåt = konkav = konvex uppåt

Skillnaden mellan konkava och konvexa funktioner visas tydligare om vi tittar på en graf. Lägg märke till hur den konvexa funktionen öppnar sig uppåt, medan den konkava funktionen öppnar sig nedåt.

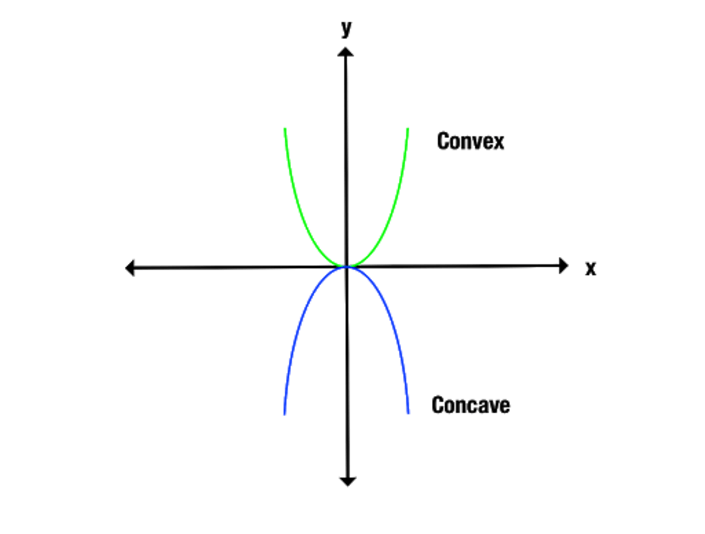
Ett annat sätt att identifiera konkava och konvexa funktioner är att koppla samman punkter på grafen längs x-axeln. En konkav funktion förbinder endast linjer under grafen, medan en konvex funktion endast ger linjer över grafen.

Vi kan dessutom använda kalkyl för att tyda om en funktion är konvex eller konkav. Om den andra derivatan av f(x) är större än noll är funktionen konvex. Men om den andra derivatan av f(x) är mindre än noll är funktionen konkav.

Konvexa vs konkava polygoner

Ingen panik, men orden konvex och konkav används även för geometri också. Konvexa och konkava former diskuteras oftast med hänvisning till polygoner, som är former med minst tre sidor och vinklar.

Regulära polygoner finns med lika sidor och vinklar, men konvexa och konkava polygoner är lite mer komplicerade. Konvexa polygoner innehåller inre vinklar som är mindre än 180 grader, medan konkava polygoner innehåller en eller flera inre vinklar som är större än 180 grader.

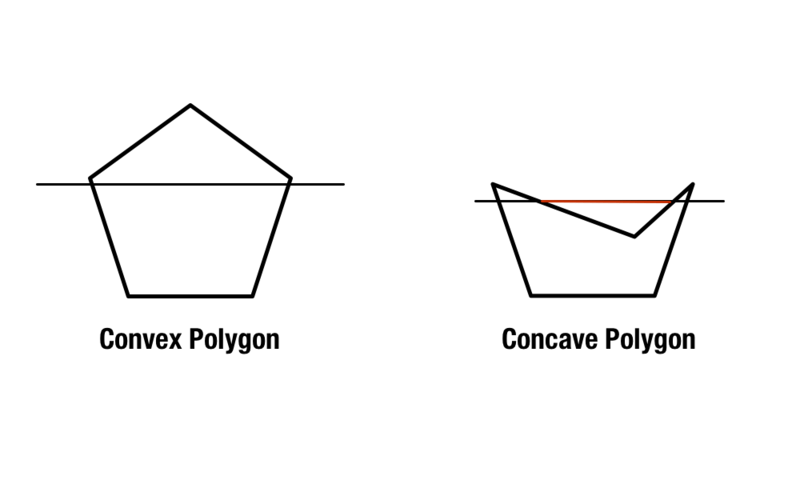
En andra metod för att identifiera konkava och konvexa polygoner är att dra två diagonala linjer tvärs över formen, med utgångspunkt från formens hörn. Om varje linje finns inom formen är formen konvex. Om det finns minst en linje som korsar utanför formen är den konkav.

Konkava vs konvexa speglar

Vorden konkav och konvex används ofta när man diskuterar optiska föremål, som speglar och linser. Varje konvex yta kommer att sticka utåt, likt en bubbla, vilket ger effekten av bredd. Konvexa speglar är vanliga i parkeringsgarage, där förare behöver en vidsträckt vy runt hörn eller potentiella döda vinklar.

En konkav spegel är däremot böjd inåt och ger en förstorad reflektion som är upp och ner. Som University of South Wales’ School of Physics har visat kan vem som helst med en blank sked testa denna observation genom att titta på sin spegelbild i skeden. På skedens konkava yta, där du plockar upp din mat, förvrängs din spegelbild på ett smalt sätt, och du kommer att framstå som uppochnedvänd. Men om du vänder skeden till den konvexa sidan kommer din spegelbild att vara upprätt och mindre.

Reflexioner varierar så mycket mellan konvexa och konkava ytor därför att oavsett om ytan kröker utåt eller inåt är själva spegeln en del av en sfär. Eftersom en sfärs yta inte är platt kommer det ljus som reflekteras från dess yta att färdas olika långt innan det kommer i kontakt med spegeln.

Avhängigt av vilket område av ytan som ljuset kommer i kontakt med kan en ljusstråle reflekteras av närliggande ytor för att skapa ett mer fokuserat synligt område. Detta är anledningen till att man, när man tittar på insidan av en sked, kanske bara ser reflektionen av det som är närmast skedens yta – även om den fortfarande verkar mindre. Om man dessutom skulle placera sitt finger inuti skeden kan spegelytan ge upphov till två eller tre olika reflektioner samtidigt.

Konkav lins vs konvex lins

Konkava och konvexa linser finns i vardagliga föremål som glasögon, kontaktlinser, kikare och teleskop. På samma sätt som vetenskapen bakom ljusreflektion på konvexa och konkava speglar finns det också mönster för hur ljus passerar genom konkava och konvexa linser för att producera en synlig bild.

Konvexa linser

Enligt Manocha Academy kallas konvexa linser för konvergerande linser på grund av deras förmåga att producera bilder som är förminskade, förstorade eller introverta. Hur exakt en bild framträder genom den konvexa linsen beror på hur nära föremålet är objektivets brännpunkt. För varje konvex lins finns det symmetriska brännpunkter på vardera sidan av linsen.

Hur exakt ett objekt framställs genom en konvex lins förutsägs med hjälp av tre principer:

Princip 1: Varje ljusstråle som passerar genom en konvex lins är parallell med huvudaxeln, som är en centrallinje som går genom det absoluta centrumet av en sfärisk lins. När ljuset väl kommer i kontakt med linsen bryts ljuset och passerar genom brännpunkten på andra sidan. Passerande ljusstrålar som är parallella med huvudaxeln rör sig ovanför objektet framför linsen.

Princip 2: Varje ljusstråle som passerar genom centrum av en konvex lins fortsätter i en rak linje på andra sidan.
Princip 3: Varje ljusstråle som passerat genom en brännpunkt på samma sida som objektet kommer att brytas vid kontakt med linsen och bli parallell med huvudaxeln på andra sidan.

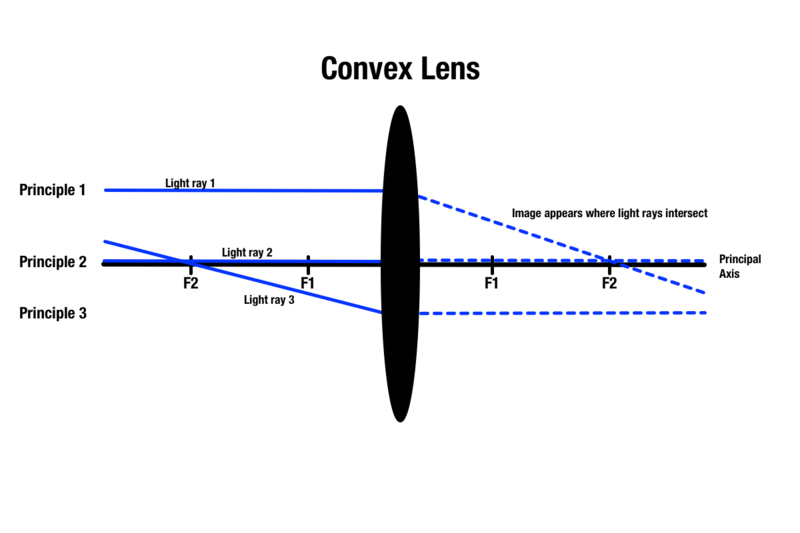
Men även om det finns tre principer för att förutsäga bildkvaliteten genom en konvex lins, så är det bara två principer som kan tillämpas på ett objekt när man ritar ett stråldiagram. Två principiella principer ger upphov till en ljuskorsning på andra sidan linsen, vilket anger det område där objektets bild framträder.

Desto längre bort ett föremål befinner sig från en konvex lins, desto mindre blir bilden på andra sidan, och ju närmare ett föremål befinner sig från den konvexa linsen, desto större kommer det att synas. Ett objekt som befinner sig bortom den närmaste brännpunkten ger en större bild bakom objektet. Som Manocha Academy påpekar används denna typ av linsförstoring för optiska verktyg som förstoringsglas.

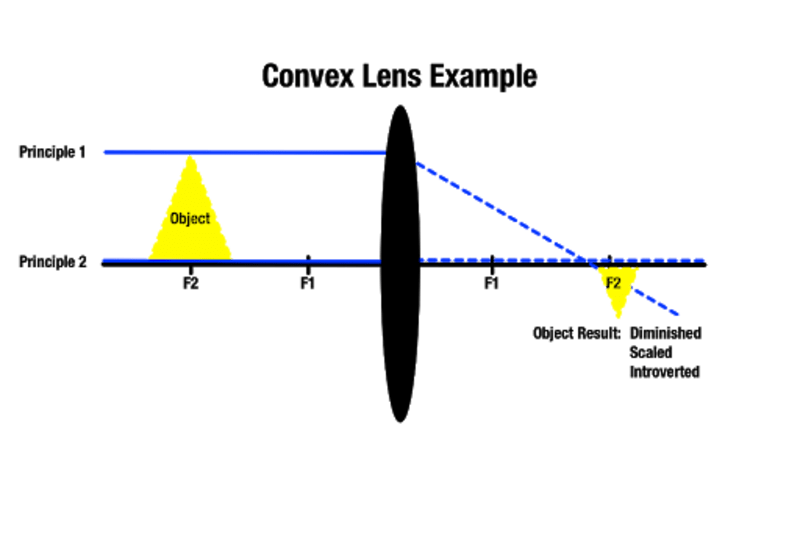
Avhängigt av vilken brännpunkt ett objekt är placerat är det möjligt att producera en bild som är ungefärlig i storlek. Det är också möjligt att skapa verkliga bilder som inte är synliga om de passerande ljusstrålarna aldrig skär varandra eftersom de är parallella på andra sidan. I detta fall existerar den bild som produceras på ett oändligt avstånd.

Konkava linser

Alla konkava linser kommer att ha en tjockare diameter och ett tunnare centrum eftersom en konkav lins är krökt inåt. Formen på konkava linser gör att ljuset sprids ut när det kommer i kontakt med linsen, vilket gör att virtuella objekt ser mindre ut. Den konkava linsens förmåga att sprida ut ljuset gör den till en idealisk lins för verktyg som ficklampor, där en central ljuskälla kan användas över en större yta.

Konkava linser producerar bilder med tre principer som liknar konvexa linser:

Princip 1: Varje ljusstråle som rör sig ovanför objektet och parallellt med huvudaxeln kommer att brytas vid kontakt med linsen och verka som om den kommer från riktningen av den närmaste brännpunkten.

Princip 2: Varje ljusstråle som passerar genom den konkava linsens centrum kommer att passera utan brytning.
Princip 3: Varje ljusstråle som riktas mot en brännpunkt på andra sidan av den konkava linsen kommer att brytas och bli parallell med huvudaxeln.

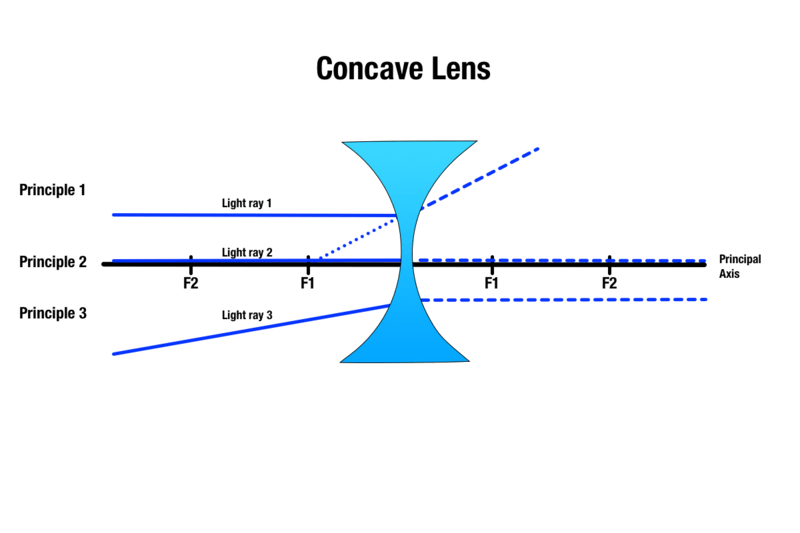
Men även om storleken på objektets bild kommer att variera beroende på objektets avstånd från en konkav lins, så är den bild som produceras alltid virtuell, upprätt, mindre och visas på samma sida av linsen som objektet.

Konkav vs. konvex i skrift

Vorden konkav och konvex är motsatser till varandra, och de beskriver i huvudsak formen på föremål eller ytor på samma sätt som vi kontrasterar ord som:

• Små vs. big
• Tall vs. short
• Slim vs. wide
• Round vs. flat

Om att konkava och konvexa är tekniska ord kan användningen av dem beskrivande för prosa ge en mer metaforisk eller abstrakt tolkning för en tillfällig publik. Detta innebär att om författare bestämmer sig för att använda konkava eller konvexa utanför deras typiska användningsområde måste författaren avgöra hur tydlig han/hon vill att skrivandet ska vara.

Konsumerar adjektivet

Ett framträdande exempel på användning av konkav eller konvex i litteraturen är att betrakta den amerikanske författaren David Foster Wallaces (eller DFW förkortat) skrifter. DFW är ökänd för sin komplexa och tekniska skrivstil – och ja, han använde konvex och konkav för att beskriva substantiv flera gånger. Wallace använder konkav och konvex i följande exempel:

”Mitt handöga var okej, men jag var varken stor eller snabb, hade ett nästan konkavt bröst och handleder som var så tunna att jag kunde armbinda dem med en tumme och en lillfinger…”.

– ”Tennis, trigonometri, tornados: A Midwestern Boyhood”, Harper’s Magazine.

”…dockögon som öppnas med ett drag i en hjärtsträng, konkava där jag är konvex.”

– ”Order and Flux in Northampton,” Conjunctions.

Punkten med att använda DFW-exempel är inte bara att visa hur författare har använt konvex eller konkav utanför matematiska sammanhang, utan snarare att författare ska överväga om det är bra att använda tekniska eller abstrakta termer för att tydligt kommunicera med sin publik.
I det första DFW-exemplet är användningen av konkav meningsfull eftersom han beskriver strukturen hos något. Men att använda konkava och konvexa för att beskriva icke objektiva substantiv, såsom känslor eller tankar, tenderar att skymma innebörden av det vi försöker förklara. Det andra DFW-exemplet går på en hårfin linje när man använder konvexa och konkava eftersom deras användning är både bokstavlig och metaforisk.

FAQ:

Vad är en funktion?

En funktion är ekvationen för en linje i en graf. Funktioner är olika för varje linje på en graf, men de har den allmänna formen,

f(x) = x + 1

Med en linjefunktion är den beroende variabeln vanligtvis f(x), medan varje okänd variabel inom funktionen kallas oberoende variabel.

Vad är domänen?

Domänen är en uppsättning oberoende variabler på en graf som motsvarar linjens funktion. Domäner är viktiga att förstå eftersom de lokaliserar specifika punkter på diagrammet som motsvarar varje verklig utgång av en ekvation.

Vad är intervallet?

Att intervallet för en funktion representerar alla möjliga värden längs x- eller y-axeln på en graf som ger ett giltigt värde för den beroende variabeln. Alla lägsta och högsta heltal identifieras genom att ersätta x- eller y-axeln med variabler.

Vad är ett intervall?

Ett intervall är en uppsättning tal som representerar en linjes helheter, även kallad domänen. Ett slutet intervall omfattar två ändliga punkter på en linje, där linjen inte längre existerar utanför ett heltalsområde. Ett öppet intervall är en uppsättning heltal som inte representerar det absoluta slutet av en linjes domän.

Testa dig själv!

Se hur väl du förstår skillnaden mellan konvex och konkav med följande flervalsfrågor:

1. När du tittar på en glänsande sked märker du att din spegelbild är upp och ner. Skedens yta är en _________ yta.
   a. Konvex
   b. Spegel
   c. Konkav
   d. Metall
2. När det gäller grafiska funktioner kallas en konvex funktion ibland för:
   a. Konkav uppåt
   b. Konvex nedåt
   c. Konkav nedåt
   d. A och B
3. Vilket av följande beskriver inte en konkav yta:
   a. Håligt halvklot
   b. Ögonlins
   c. Spannmålsskål
   d. Hemisfär
4. Vilket av följande beskriver inte en konvex yta:
   a. Karaktären Stewie från Family Guy
   b. Sfär
   c. Parkeringsgarage spegel
   d. Fotboll
5. Vilken av följande former kan inte existera som en konkav polygon:
   a. Pentagon
   b. Hexagon
   c. Triangel
   d. Octagon

Svar

1. C: Konkav
2. D: A och B
3. D: Halvklot
4. B: Sfär
5. C: Triangel

Källor:

1. Bourne, M. ”Domain and Range of a Function”. Interactive Mathematics, 4 januari 2019.
2. ”Konkav”. Merriam-Webster Dictionary, 2019.
3. ”Concave.” The Oxford Dictionary of Word Histories, Ed. Chantrell, 2002, s. 110.
4. ”Konkava och konvexa speglar”. Manocha Academy, YouTube, 2019.
5. ”Konkav lins: Definition & Användning.” Study.com, 2019.
6. ”Konvex.” Merriam-Webster Dictionary, 2019.
7. ”Konvexa och konkava linser”. Manocha Academy, YouTube, 2019.
8. ”Matematik / Förstå polygoner”. Learnhive Inc., 2018.
9. ”Reflektion från en konkav spegel”. UNSW Physics, YouTube, 2017.
10. Wallace, D.F. ”Tennis, trigonometri, tornados: A Midwestern Boyhood.” Harper’s Magazine, 1991.
11. Wallace, D.F. ”Order and Flux in Northampton”. Conjunctions, 1991.
12. Weisstein, Eric W. ”Concave Function”. MathWorld-A Wolfram Web Resource, n.d.

Weisstein, Eric W. ”Convex Function.” MathWorld-A Wolfram Web Resource, n.d.

The Word Counter är ett dynamiskt online-verktyg som används för att räkna ord, tecken, meningar, stycken och sidor i realtid, tillsammans med stavnings- och grammatikkontroll.