Introduktion till affärsstatistik

Observera följande datamängd.
4; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7; 7; 7; 8; 8; 8; 8; 9; 10

Denna datamängd kan representeras av följande histogram. Varje intervall har bredd ett, och varje värde ligger i mitten av ett intervall.

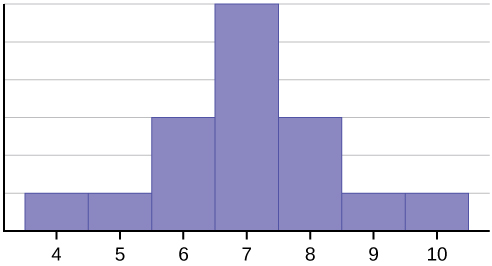
Histogrammet visar en symmetrisk fördelning av data. En fördelning är symmetrisk om en vertikal linje kan dras vid någon punkt i histogrammet så att formen till vänster och höger om den vertikala linjen är spegelbilder av varandra. Medelvärdet, medianen och modus är vardera sju för dessa data. I en perfekt symmetrisk fördelning är medelvärdet och medianen lika stora. Detta exempel har ett modus (unimodal), och modus är detsamma som medelvärde och median. I en symmetrisk fördelning som har två modus (bimodal) skulle de två modus vara olika från medelvärdet och medianen.

Histogrammet för data: 4566677778 är inte symmetriskt. Den högra sidan verkar ”avhuggen” jämfört med den vänstra sidan. En fördelning av den här typen kallas sned åt vänster eftersom den dras ut åt vänster. Vi kan formellt mäta skevheten hos en fördelning på samma sätt som vi matematiskt kan mäta dataens centrumvikt eller dess allmänna ”snabbhet”. Den matematiska formeln för skevhet är: . Ju större avvikelsen från noll är, desto större är skevheten. Om skevheten är negativ är fördelningen snedställd åt vänster som i (figur). Ett positivt mått på skevhet indikerar högerskevhet som i (figur).

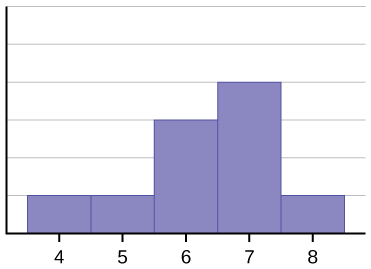
Medelvärdet är 6,3, medianen är 6,5 och modus är sju. Lägg märke till att medelvärdet är mindre än medianen och att de båda är mindre än modus. Både medelvärdet och medianen återspeglar skevheten, men medelvärdet återspeglar den i högre grad.

Histogrammet för data: 67777888910, är inte heller symmetriskt. Det är skevt åt höger.

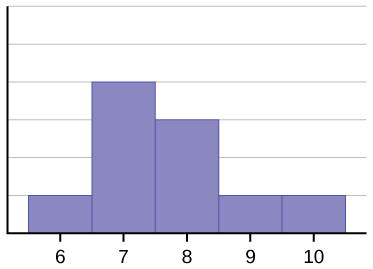
Medelvärdet är 7,7, medianen är 7,5 och modus är sju. Av de tre statistiska uppgifterna är medelvärdet det största, medan modet är det minsta. Återigen återspeglar medelvärdet snedfördelningen mest.

För att sammanfatta, i allmänhet om fördelningen av data är snedfördelad åt vänster, är medelvärdet mindre än medianen, som ofta är mindre än modet. Om fördelningen av data är skev till höger är modet ofta mindre än medianen, som är mindre än medelvärdet.

Som med medelvärdet, medianen och modet, och som vi kommer att se inom kort, variansen, finns det matematiska formler som ger oss exakta mått på dessa egenskaper hos fördelningen av data. Om vi återigen tittar på formeln för skevhet ser vi att detta är ett förhållande mellan dataens medelvärde och de enskilda observationerna i kubik.

där är dataens standardavvikelse i urvalet, , och är det aritmetiska medelvärdet och är urvalsstorleken.

Formellt sett är det aritmetiska medelvärdet känt som det första momentet i fördelningen. Det andra momentet vi kommer att se är variansen, och skevhet är det tredje momentet. Variansen mäter de kvadrerade skillnaderna mellan data och medelvärdet och skewness mäter de kubiska skillnaderna mellan data och medelvärdet. Medan variansen aldrig kan vara ett negativt tal kan skewness-måttet vara det, och det är så här vi avgör om uppgifterna är skeva åt höger eller vänster. Snedheten för en normalfördelning är noll, och alla symmetriska data bör ha en snedhet nära noll. Negativa värden för skewness indikerar data som är skeva åt vänster och positiva värden för skewness indikerar data som är skeva åt höger. Med skev vänster menar vi att den vänstra svansen är lång i förhållande till den högra svansen. På samma sätt betyder snedställd höger att den högra svansen är lång i förhållande till den vänstra svansen. Snedhet karakteriserar graden av asymmetri i en fördelning kring dess medelvärde. Medan medelvärdet och standardavvikelsen är dimensionella storheter (det är därför vi tar kvadratroten av variansen ), dvs. har samma enheter som de uppmätta storheterna , definieras skewness konventionellt på ett sådant sätt att den blir icke-dimensionell. Det är ett rent tal som endast karaktäriserar fördelningens form. Ett positivt värde på skewness betecknar en fördelning med en asymmetrisk svans som sträcker sig ut mot mer positiva X och ett negativt värde betecknar en fördelning vars svans sträcker sig ut mot mer negativa X. Ett nollmått på skewness anger en symmetrisk fördelning.

Skewness och symmetri blir viktiga när vi diskuterar sannolikhetsfördelningar i senare kapitel.