The Toom-Cook Algorithm
Här lär vi oss en genial tillämpning av en divide and conquer-algoritm i kombination med linjär algebra för att multiplicera stora tal snabbt. Och en introduktion till big-O-notationen!
Detta resultat är faktiskt så kontraintuitivt att den store matematikern Kolmogorov förmodade att en så snabb algoritm inte existerade.
Del 0: Lång multiplikation är långsam multiplikation. (Och en introduktion till Big-O Notation)
Vi minns alla att vi lärde oss att multiplicera i skolan. Jag har faktiskt en bekännelse att göra. Kom ihåg att detta är en zon utan domar 😉
I skolan hade vi ”våtlek” när det regnade för mycket för att leka på lekplatsen. Medan andra (normala/roliga/älskande/positiva-adjektiv-av-valet) barn lekte lekar och strulade runt, tog jag ibland ett pappersark och multiplicerade stora tal tillsammans, bara för skojs skull. Den rena glädjen att räkna! Vi hade till och med en multiplikationstävling, ”Super 144”, där vi var tvungna att multiplicera ett 12 gånger 12 rutnät av siffror (från 1 till 12) så snabbt som möjligt. Jag tränade detta religiöst, till den grad att jag hade mina egna förberedda övningsark som jag kopierade och sedan använde i tur och ordning. Så småningom fick jag ner min tid till 2 minuter och 1 sekund, då min fysiska gräns för klotter var nådd.
Trots denna besatthet av multiplikation föll det mig aldrig in att vi kunde göra det bättre. Jag tillbringade så många timmar med att multiplicera, men jag försökte aldrig förbättra algoritmen.
Tänk på att multiplicera 103 med 222.
Vi beräknar 2 gånger 3 gånger 1 + 2 gånger 0 gånger 10 + 2 gånger 1 gånger 100 + 20 gånger 3 gånger 1 + 20 gånger 0 gånger 10 + 20 gånger 1 gånger 100 = 22800
I allmänhet krävs det O(n²) operationer för att multiplicera till n siffror. Notationen ”big-O” innebär att om vi skulle grafera antalet operationer som en funktion av n, så är det n²-termen som verkligen är det viktiga. Formen är i huvudsak kvadratisk.
I dag ska vi uppfylla alla våra barndomsdrömmar och förbättra denna algoritm. Men först! Big-O väntar på oss.
Big-O
Se på de två graferna nedan

Fråga en matematiker: ”Är x² och x²+x^(1/3) samma sak?”, och han eller hon kommer förmodligen att spy i sin kaffekopp och börja gråta och mumla något om topologi. Det var åtminstone min reaktion (till en början), och jag vet knappast något om topologi.
Okej. De är inte samma sak. Men vår dator bryr sig inte om topologi. Datorer skiljer sig åt i prestanda på så många sätt som jag inte ens kan beskriva eftersom jag inte vet något om datorer.
Men det är ingen idé att finjustera en ångvält. Om två funktioner, för stora värden på deras indata, växer i samma storleksordning så innehåller det för praktiska ändamål den mesta relevanta informationen.
I grafen ovan ser vi att de två funktionerna ser ganska lika ut för stora indata. Men på samma sätt liknar x² och 2x² varandra – den senare är bara dubbelt så stor som den förra. Vid x = 100 är den ena 10 000 och den andra 20 000. Det betyder att om vi kan beräkna den ena kan vi förmodligen beräkna den andra. Medan en funktion som växer exponentiellt, säg 10^x, vid x = 100 redan är långt mycket större än antalet atomer i universum. (10¹⁰⁰ >>>>> 10⁸⁰ vilket är en uppskattning, Eddington-talet, på antalet atomer i universum enligt min Googling*).
*Jag använde faktiskt DuckDuckGo.
Skriva heltal som polynom är både mycket naturligt och mycket onaturligt. Att skriva 1342 = 1000 + 300 + 40 + 2 är mycket naturligt. Att skriva 1342 = x³+3x²+4x + 2, där x = 10, är något udda.
Genomgående antar vi att vi vill multiplicera två stora tal, skrivna i basen b, med n siffror vardera. Vi skriver varje n-siffrigt tal som ett polynom. Om vi delar upp det n-siffriga talet i r bitar har detta polynom n/r termer.
Till exempel, låt b = 10, r = 3 och vårt tal är 142 122 912
Vi kan omvandla detta till
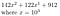
Det här fungerar mycket bra när r = 3 och vårt tal, skrivet i bas 10, hade 9 siffror. Om r inte perfekt delar n kan vi bara lägga till några nollor längst fram. Återigen illustreras detta bäst med ett exempel.
27134 = 27134 + 0*10⁵ = 027134, vilket vi representerar som
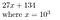
Varför kan detta vara till hjälp? För att hitta koefficienterna till polynomet P, om polynomet är av ordning N, kan vi bestämma dess koefficienter genom att ta stickprov i N+1 punkter.
Till exempel, om polynomet x⁵ + 3x³ +4x-2, som är av ordning 5, provtas i 6 punkter kan vi sedan räkna ut hela polynomet.
Intuitivt har ett polynom av ordning 5 6 koefficienter: koefficienten för 1, x, x², x³, x⁴, x⁵. Givet 6 värden och 6 okända kan vi ta reda på värdena.
(Om du kan linjär algebra kan du behandla de olika potenserna av x som linjärt oberoende vektorer, göra en matris för att representera informationen, invertera matrisen och voila)
Sampling av polynom för att bestämma koefficienter (valfritt)
Här tittar vi lite djupare på logiken bakom att ta prover på ett polynom för att härleda dess koefficienter. Hoppa gärna över till nästa avsnitt.
Vad vi kommer att visa är att om två polynom av grad N stämmer överens på N+1 punkter så måste de vara likadana. D.v.s. N+1 punkter specificerar unikt ett polynom av grad N.
Tänk på ett polynom av grad 2. Detta är av formen P(z) = az² +bz + c. Genom algebrans fundamentala sats – skamlös, plug här, jag tillbringade flera månader med att sammanställa ett bevis för detta, och sedan skriva upp det, här – kan detta polynom vara faktoriserat. Det betyder att vi kan skriva det som A(z-r)(z-w)
Bemärk att vid z = r, och vid z = w, värderas polynomet till 0. Vi säger att w och r är rötter till polynomet.
Nu visar vi att P(z) inte kan ha mer än två rötter. Anta att det har tre rötter, som vi kallar w, r, s. Vi faktoriserar sedan polynomet. P(z) = A(z-r)(z-w). Då är P(s) = A(s-r)(s-w). Detta är inte lika med 0, eftersom multiplikation av tal som inte är noll ger ett tal som inte är noll. Detta är en motsägelse eftersom vårt ursprungliga antagande var att s var en rot i polynomet P.
Detta argument kan tillämpas på ett polynom av ordning N på ett i stort sett identiskt sätt.
Antag nu att två polynom P och Q av ordning N stämmer överens på N+1 punkter. Om de är olika är då P-Q ett polynom av ordning N som är 0 i N+1 punkter. Enligt det föregående är detta omöjligt, eftersom ett polynom av ordning N har högst N rötter. Vårt antagande måste alltså ha varit fel, och om P och Q stämmer överens i N+1 punkter är de samma polynom.
Seeing is believing: I bas 10 är p 24 siffror långt (n=24), och vi kommer att dela upp det i fyra delar (r=4). n/r = 24/4 = 6
p = 292 103 243 859 143 157 364 152.
Och låt det polynom som representerar det kallas P,
P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152
med P(10⁶) = p.
Då graden av detta polynom är 3 kan vi räkna ut alla koefficienter genom att ta stickprov på 4 ställen. Låt oss få en känsla för vad som händer när vi tar stickprov på några punkter.
- P(0) = 364 152
- P(1) = 1 043 271
- P(-1) = 172 751
- P(2) = 3 962 726
En slående sak är att dessa alla har 6 eller 7 siffror. Det kan jämföras med de 24 siffror som ursprungligen fanns i p.
Låt oss multiplicera p med q. Låt q = 124 153 913 241 143 634 899 130, och
Q(x) = 124 153 x³ + 913 241 x²+143 634 x + 899 130
Att räkna ut t=pq kan vara hemskt. Men i stället för att göra det direkt försöker vi beräkna polynomrepresentationen av t, som vi kallar T. Eftersom P är ett polynom av ordningen r-1=3 och Q är ett polynom av ordningen r-1=3, är T ett polynom av ordningen 2r-2=6.
T(10⁶) = t = pq
T(10⁶) = P(10⁶)Q(10⁶)
Tricket är att vi kommer att räkna ut T:s koefficienter i stället för att direkt multiplicera p och q tillsammans. Då är det lätt att beräkna T(1⁰⁶), eftersom vi för att multiplicera med 1⁰⁶ bara sätter 6 nollor på baksidan. Att summera alla delar är också enkelt eftersom addition är en mycket billig åtgärd för datorer att utföra.
För att beräkna T:s koefficienter måste vi ta stickprov i 2r-1 = 7 punkter, eftersom det är ett polynom av ordning 6. Vi vill förmodligen välja små heltal, så vi väljer
- T(0)=P(0)Q(0)= 364 152*899 130
- T(1)=P(1)Q(1)= 1 043 271*2 080 158
- T(2)=P(2)Q(2)= 3 962 726*5 832,586
- T(-1)=P(-1)Q(-1)= 172751*1544584
- T(-2)=P(-2)Q(-2)= -1 283 550*3 271,602
- T(3)=P(-3)Q(-3)= -5,757,369*5,335,266
Notera storleken på P(-3), Q(-3), P(2), Q(2) etc… Dessa är alla tal med ungefär n/r = 24/4 = 6 siffror. En del är 6 siffror, en del är 7 siffror. När n blir större blir denna approximation mer och mer rimlig.
So långt har vi reducerat problemet till följande steg, eller algoritm:
(1) Beräkna först P(0), Q(0), P(1), Q(1), Q(1), etc. (lågkostnadsåtgärd)
(2) För att få fram våra 2r-1= 7 värden på T(x) måste vi nu multiplicera 2r-1 tal med en approximativ storlek n/r siffror långa. Vi måste nämligen beräkna P(0)Q(0), P(1)Q(1), P(-1)Q(-1) osv. (Åtgärd med hög kostnad)
(3) Rekonstruera T(x) från våra datapunkter. (Lågkostnadsåtgärd: men kommer att beaktas senare).
(4) Med vår rekonstruerade T(x), utvärdera T(10⁶) i detta fall
Detta leder på ett trevligt sätt till en analys av körtiden för denna metod.
Löptid
Från ovanstående har vi kommit fram till att, om man tillfälligt bortser från de lågkostnadsåtgärderna (1) och (3), kommer kostnaden för att multiplicera två n-siffriga tal med Tooms algoritm att lyda:
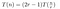
Det här är vad vi såg i det fungerande exemplet. Att multiplicera varje P(0)Q(0), P(1)Q(1) osv. kostar T(n/r) eftersom vi multiplicerar två tal med längden ungefär n/r. Vi måste göra detta 2r-1 gånger, eftersom vi vill ta ett urval av T(x) – som är ett polynom av ordningen 2r-2 – på 2r-1 ställen.
Hur snabbt är detta? Vi kan lösa denna typ av ekvation explicit.

Allt som återstår nu är några. rörig algebra
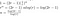
Som det fanns några andra kostnader för matrismultiplikationen (”återmontering”), och från additionen, kan vi inte riktigt säga att vår lösning är den exakta körtiden, så i stället drar vi slutsatsen att vi har hittat den stora-O av körtiden
Optimering av r
Denna körtid beror fortfarande på r. Fixa r, så är vi klara. Men vår nyfikenhet är ännu inte tillfredsställd!
När n blir stort vill vi hitta ett ungefärligt optimalt värde för vårt val av r. D.v.s. vi vill välja ett värde på r som förändras för olika värden på n.
Den viktigaste saken här är att vi, när r varierar, måste vara lite uppmärksamma på återmonteringskostnaden – den matris som utför denna operation har en kostnad på O(r²). När r var fast behöver vi inte titta på detta, eftersom när n växer sig stort med r fast, är det termerna som involverar n som bestämmer tillväxten i hur mycket beräkning som krävs. Eftersom vårt optimala val av r kommer att bli större när n blir större kan vi inte längre ignorera detta.
Denna distinktion är avgörande. Ursprungligen valde vi i vår analys ett värde på r, kanske 3, kanske 3 miljarder, och tittade sedan på big-O-storleken när n blev godtyckligt stor. Nu tittar vi på beteendet när n växer godtyckligt stort och r växer med n med en hastighet som vi bestämmer. Denna förändring av perspektivet ser på O(r²) som en variabel, medan när r hölls fast var O(r²) en konstant, om än en som vi inte kände till.
Så, vi uppdaterar vår analys från tidigare:
där O(r²) representerar kostnaden för återmonteringsmatrisen. Vi vill nu välja ett värde på r för varje värde på n som approximativt minimerar detta uttryck. För att minimera försöker vi först att differentiera med avseende på r. Detta ger det något avskyvärt utseende uttrycket

Normalt sett, för att hitta minimipunkten, sätter vi derivatan lika med 0. Men det här uttrycket har inte något fint minimum. Istället hittar vi en ”tillräckligt bra” lösning. Vi använder r = r^(sqrt(logN)) som vårt guestimatvärde. Grafiskt sett är detta ganska nära minimum. (I diagrammet nedan är faktorn 1/1000 där för att göra grafen synlig i rimlig skala)
Grafen nedan visar vår funktion för T(N), skalad med en konstant, i rött. Den gröna linjen är vid x = 2^sqrt(logN) vilket var vårt guestimatvärde. ’x’ ersätter ’r’, och i var och en av de tre bilderna används ett annat värde på N.



Detta är ganska övertygande för mig om att vårt val var ett bra val. Med detta val av r kan vi koppla in det och se hur vår algoritms slutliga big-O:

där vi helt enkelt kopplade in vårt värde för r och använde en approximation för log(2r-1)/log(r), som är mycket exakt för stora värden på r.
Hur stor är förbättringen?
Kanske var det rimligt att jag inte upptäckte denna algoritm när jag var en liten pojke som gjorde multiplikationer. I grafen nedan anger jag koefficienten för vår big-O-funktion till 10 (i demonstrationssyfte) och dividerar den med x² (eftersom det ursprungliga tillvägagångssättet för multiplikation var O(n²)). Om den röda linjen tenderar mot 0 skulle det visa att vår nya körtid asymptotiskt sett är bättre än O(n²).
Och faktiskt, även om funktionens form visar att vårt tillvägagångssätt så småningom är snabbare, och så småningom är det mycket snabbare, måste vi vänta tills vi har nästan 400 siffror långa tal för att detta ska vara fallet! Även om koefficienten bara var 5 måste siffrorna vara ungefär 50 siffror långa för att det ska bli en hastighetsförbättring.

För mig som är 10 år gammal skulle det vara lite svårt att multiplicera 400-siffriga siffror! Att hålla reda på de olika rekursiva anropen av min funktion skulle också vara något skrämmande. Men för en dator som utför en uppgift inom artificiell intelligens eller fysik är detta ett vanligt problem!
Hur djupgående är detta resultat?
Vad jag älskar med den här tekniken är att det inte är raketforskning. Det är inte den mest häpnadsväckande matematik som någonsin har upptäckts. I efterhand kanske det verkar uppenbart!
Men detta är matematikens briljans och skönhet. Jag läste att Kolmogorov vid ett seminarium gissade att multiplikation i grunden var O(n²). Kolmogorov uppfann i princip mycket av den moderna sannolikhetsteorin och analysen. Han var en av 1900-talets matematiska storheter. Men när det gällde detta orelaterade område visade det sig att det fanns en hel kunskapsmassa som väntade på att upptäckas och som satt rakt under hans och alla andras näsor!
I själva verket kommer man ganska snabbt att tänka på Divide and Conquer-algoritmerna i dag, eftersom de är så vanligt förekommande. Men de är en produkt av datorrevolutionen, eftersom det är först med den enorma beräkningskraften som mänskliga hjärnor har fokuserat specifikt på beräkningshastigheten som ett område inom matematiken som är värt att studera i sin egen rätt.
Detta är anledningen till att matematiker inte bara är villiga att acceptera att Riemannhypotesen är sann bara för att det verkar som om den skulle kunna vara sann, eller att P inte är lika med NP bara för att det verkar mest sannolikt. Matematikens underbara värld har alltid en förmåga att förvirra våra förväntningar.
Det går faktiskt att hitta ännu snabbare sätt att multiplicera. De för närvarande bästa tillvägagångssätten använder snabba fouriertransformationer. Men det sparar jag till en annan dag 🙂
Låt mig veta vad ni tycker nedan. Jag finns nyligen på Twitter som ethan_the_mathmo, du kan följa mig här.
Jag stötte på det här problemet i en underbar bok som jag använder och som heter ”The Nature of Computation” av fysikerna Moore och Mertens, där ett av problemen vägleder dig genom att analysera Tooms algoritm.