Hur man hjälper elever som kämpar med ordproblem

”De kan matematiken. De kan bara inte lösa ordproblemen. Det är deras läsförståelse.”

Mrs Hartwell förklarade varför hennes elever hade haft problem på de statliga proven. Hon kände sina elever och hade gjort omfattande bedömningar. Hon var säker på att deras svårigheter var ett läs- och skrivproblem.

”Jag förstår inte varför de gör läsningen så svår. Barnen gör redan ett test i språkkunskap.”

Jag hade matchats med fru Hartwell (och andra på hennes skola) som en del av ett program i New York som syftade till att förbättra resultaten i matematik. Målet var att införa konceptuell matematik i ”Tier 1”-skolor. Tier 1-skolor var de skolor som ledde staden på tre områden. Lägsta inkomst, lägsta provresultat och högsta andel färgade elever.

Jag hade hört förklaringen om ”läs- och skrivkunnighet” från andra lärare i programmet. Och det var logiskt. Om eleverna kunde matematiken, varför hade de annars svårt att klara provet, som innehöll många ordproblem?

Men det fanns en hake. Under de senaste tre åren hade läs- och skrivkunnigheten ökat från 30-40 % i hela staden. Under samma period hade resultaten i matematik varit i stort sett oförändrade.

Om detta var ett läsproblem borde ökningar av läsresultaten leda till en explosiv tillväxt i matematik. Dessutom verkade språket i ordproblemen inte tillräckligt komplicerat för att orsaka problem.

Nästa period skulle jag besöka Ms Hartwells klass. Hon hade planerat en lektion om ordproblem, så jag kunde se problemet med egna ögon.

Over-Scaffolding Word Problems

Elverna satt vid runda bord och hon stod längst fram. Hon och hennes elever hade alla handhållna whiteboards.

De öppnade sina läroböcker på sidan 47 och hon läste ett ordproblem högt. ”Sarah har 40 pund morötter till sina hästar. Om hon har 100 hästar, hur många pund får varje häst?”.

”Okej klass, hon har 40 pund som hon kommer att ge till varje häst. Så vilken operation behöver vi?”

Hon pekade på ett ankardiagram som listar ”nyckelorden” för varje operation. ’Var och en’ stod högst upp på listan över indelning.

”Indelning!” svarade klassen.

”Just det. Så hur delar vi ett litet tal med ett stort tal?”

Klassen var tyst. Ms Hartwell ritade ett vinculum (hus för lång division) på sin whiteboardtavla. Eleverna kopierade när hon satte 40 under huset och 100 utanför.

”Nu ryms inte 100 i 40, så vi måste lägga till en decimal”. Hon ändrade 40 till 40,0. ”Hur många gånger går 100 in i 400?”

Ett par elever ropade ”fyra!”.

”Exakt. Nu måste vi sätta en decimal i vår kvot också. Vårt slutliga svar är?”

Klassen läste svaret, ”0,4”, från hennes whiteboard.

Hon tilldelade ett liknande problem och pekade på ”CUBES”-affischen på väggen. ”Kom ihåg att sätta cirklar runt siffrorna och sätta rutor för nyckelorden.”

Hon cirkulerade medan eleverna arbetade. Några frågade var man skulle sätta decimalen. Andra hade problem med att rada upp subtraktionsdelen av den långa divisionen. Vissa elever arbetade i par, där en gjorde beräkningen medan den andra kopierade.

I slutet av lektionen hade alla rätt svar på sina papper. ”Ser du?” Ms Hartwell påpekade: ”Alla kan räkna.”

Vad gick fel?

Det här är ett extremt exempel, men många av de misstag som Ms Hartwell gjorde är faktiskt ganska vanliga.

Over-scaffolding inträffar när vi ger eleverna för mycket stöd. Även om det är vanligt att pedagoger är stolta över att ge eleverna ”så mycket stöd som de behöver”, är det annorlunda att ge för mycket stöd.

Uttrycket ”scaffolding” kommer från Lev Vygotskijs arbete. Han myntade begreppet ”zonen för proximal utveckling”. ZPD omfattar saker som ligger precis utanför en inlärares räckvidd. De kan inte riktigt göra det på egen hand, men de kan göra det med stöd. Med hjälp av ”scaffolding” kan vi flytta dessa färdigheter till en inlärares grundläggande färdigheter.

Det som ofta glöms bort är att scaffolding endast gäller färdigheter som redan finns i en inlärares ZPD. Det finns en hel rad färdigheter som för närvarande ligger utanför en inlärares räckvidd. När vi försöker att ställa in dessa färdigheter gör vi mer skada än nytta.

Ett problem med överdriven ställningsreglering är att eleverna aldrig internaliserar de målinriktade färdigheterna. När vi hjälper en elev med något som ligger utanför deras ZPD kommer de alltid att behöva vår hjälp. Åtminstone tills vi identifierar de mellanliggande färdigheter som ligger inom deras ZPD.

Ett annat problem är att överdriven inlärning ger oss en falsk känsla av framgång. I det här fallet trodde fru Hartwell att hennes elever kunde ”göra matematiken” i ordproblemet. I verkligheten imiterade de bara hennes handlingar. Det fanns ingen anledning att tro att de skulle kunna hitta en liknande lösning på egen hand.

Hon tog också bort hela processen med ”formulering” från problemlösningsprocessen. Många pedagoger anser att förståelse och formulering är samma sak, men formulering är en separat matematisk kompetens.

Och det kan vara den ingrediens som saknas i det sätt du för närvarande undervisar i ordproblem.

Klassrumsresurser och professionellt lärande

Formulering: Nyckeln till framgång med ordproblem

Formulering av ordproblem innebär att man måste förstå dem. Men det går längre än så. Formulering liknar mer översättning än förståelse.

När en elev läser ett ordproblem måste eleven först omvandla bokstäver till ljud (avkodning). Sedan måste de förstå vad orden betyder (ordförråd). De måste förstå hur orden passar ihop i en mening (syntax). Slutligen kommer förståelsen från att sätta ihop dessa delar till en mening.

De flesta elever i sjätte klass skulle kunna läsa Ms Hartwells problem och lätt förstå att Sarah delar ut morötter till sina hästar. Men betydligt färre kommer att koppla ”delandet” av morötter till division.

Det här är den del som gör många pedagoger nervösa. Den verkar så självklar för oss. ”Hon delar bokstavligen upp morötterna. Hur kan de inte se att det är delning?”.

De gör det helt enkelt inte. Om de gjorde det skulle du inte se nyckelordstavlor hänga i matematikklassrummen. Och allt går tillbaka till när vi först lär ut operationer.

Varför eleverna kämpar med formuleringen

Många lärare i många skolor lär eleverna att matematik är ett ämne för meningsskapande. Men i andra skolor lär man ut matematik som ett ämne som handlar om att komma ihåg.

Ett exempel på ”matematik som minnesämne” är när elever memorerar matematiska fakta. Men algoritmer handlar också om att komma ihåg. Lägg 120 ovanpå 47. Följ dessa steg för att addera, dessa för att subtrahera subtrahera och dessa för att multiplicera.

Elverna kan upprepa dessa steg utan att förstå storleken på talen eller ens vad operationerna betyder.

När vi börjar med begrepp (genom att använda visuella modeller eller talsatser) lär sig eleverna vad operationerna betyder. När vi går direkt till en algoritm tänker eleverna på operationerna som en serie slumpmässiga steg.

År efter år får vi eleverna att komma ihåg och upprepa. De genomför samma algoritm 30 gånger som läxa. Ändra siffrorna och processen förblir densamma. Men ge dem ett ordproblem, och nu måste de förstå.

Vad testerna berättar om resonemang

Vi skulle kunna ge våra elever 10 problem med rubriken ”Division Word Problems”, för att göra det lättare. De kommer inte ens att behöva läsa problemen. De behöver bara räkna ut (eller gissa) vilket tal som är divisorn och vilket som är utdelningen.

Men när eleverna sitter på ett statligt prov är målet inte att göra det lättare. Målet är att bedöma vad de kan göra på egen hand.

Det är inte meningen att provtillverkarna ska tala om för dem vilken operation de ska använda. De lägger till och med in nyckelord för division och addition i samma problem. ”Det finns 20 elever i klassen. Om varje barn har tre dollar, hur mycket har de då totalt?”.

Så när eleverna kämpar med ordproblem handlar det inte bara om ordproblemen. Det betyder oftast att de gör matte med hjälp av minnet. Vi måste lära dem att matematik handlar om att skapa mening.

Studenter behöver strategier och processer för att lösa ordproblem

En del av problemet med ett system som CUBES är att det kallar sig självt för en strategi, men att det egentligen är en process.

En process är en serie av steg. När man väl har identifierat en effektiv process kan man upprepa den om och om igen utan att tänka särskilt mycket på det. Algoritmer är en process. Liksom att ställa upp sig ”från den längsta till den kortaste” för promenaden till lunchen.

En strategi är annorlunda. Strategier kräver djup förståelse. Och förmågan att tillämpa förståelsen i nya situationer.

Vi kan inte förbereda eleverna för varje scenario som de kommer att stöta på i ett ordproblem. Vissa kräver att de kombinerar olika matematiska färdigheter som de aldrig tidigare har kombinerat. Eller de kan kräva att eleverna ändrar ordningen på stegen för att komma fram till den rätta lösningen.

Tänk på följande:

Du har 5 gallon juice till ett skoldag med 100 elever. Om varje kopp innehåller 3 oz, hur många koppar kan varje elev dricka? Hur mycket kommer att bli över.

En problemlösningsprocess kan hjälpa eleverna att börja ta itu med detta problem. ”Identifiera vad som frågas.” ”Överväg vilken information som ges.”

Men det finns ingen fastställd process som vi kan lära dem att faktiskt lösa det. Det är där strategin kommer in. De måste omvandla enheter. Inse att vi dividerar med rester i stället för att dividera helt och hållet. De bör förmodligen också ordna om operationerna och dela saften i koppar innan de delar med antalet elever.

Det finns inget ”knep” som får eleverna att nå dit. De måste förstå innebörden av operationerna. De behöver förstå matematiken som ett ämne för meningsskapande. Och de behöver upprepad övning i att tillämpa strategiskt tänkande på ordproblem.

Polya-processen för att lösa ordproblem

George Pólya var en inflytelserik ungersk matematiker och Stanfordprofessor som hittade en process som kunde användas för att lösa alla problem. Hans arbete har berört otaliga matematiker och pedagoger, varav de flesta inte känner till hans namn.

I själva verket är CUBES och andra så kallade problemlösningsstrategier löst löst på hans arbete. Problemet är att de försöker förenkla det. I processen tar de bort allt som liknar djupt tänkande.

Polya trodde att varje problem kunde lösas i fyra steg: Förstå, planera, lösa och reflektera. Jag tycker att Polyas ursprungliga fyrstegsprocess är alldeles utmärkt att använda i skolor.

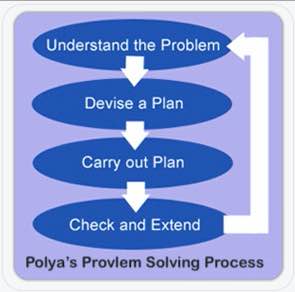För att förstå problemet identifierar vi vilken information som ges och vad vi vill hitta. Det är här som ”C” och ”U” i kuberna kommer ifrån. Om eleverna vill sätta cirklar runt siffrorna och understryka frågan går det bra. Jag föredrar att de skriver dem (med enheter) i en grafisk organisatör, åtminstone till en början. Detta hjälper dem att bearbeta det de läser. Det hjälper också mig som lärare att bedöma deras förståelse när jag går runt i rummet.

Nästan kommer den svåra delen. I ”planen” formulerar vi problemet. Vi tar ett scenario från den verkliga världen och omvandlar det till en annan matematisk representation.

Det tredje steget är att lösa problemet. Om vi har formulerat oss korrekt är det här vi beräknar. Eleverna använder vanligtvis en algoritm, men jag uppmuntrar till att använda ekvationer och visuella modeller också.

Slutligt tittar eleverna tillbaka och kontrollerar sitt arbete. De bör också reflektera över sin process. Om jag gjorde ett misstag, varför? Kan den här strategin hjälpa mig att lösa liknande problem i framtiden?

Strategier för att lösa ordproblem

Att ha en process för att närma sig ordproblem är definitivt till hjälp. Men vi kan inte låtsas att man lär sig meningsfull matematik bara genom att följa steg. Hela poängen med ordproblem är att utvidga matematiken bortom ”mattefakta” och algoritmer.

Det finns några användbara strategier för att hjälpa eleverna med formuleringen. Till en början lär jag uttryckligen ut ett antal olika strategier.

När jag lär ut strategierna låter jag eleverna lösa problem som passar bra ihop med den strategin. Vissa problemtyper passar väldigt bra med ”gissa och kontrollera”. Andra passar bättre till ”Rita en bild”.

Till slut ger jag dem utmanande ordproblem som kan lösas på flera olika sätt. När de väl har verktygen i sina verktygsbälten kan de välja vilket som är bäst för situationen.

Kombinerade strategier kan också vara mycket effektiva. Till exempel kan det ofta vara bra att rita en bild för att hjälpa till med formuleringen. Om en jordbrukare har 18 rader med morötter och 10 morötter i varje rad kan en elev börja med att rita fältet. Vid något tillfälle kanske de tänker ”Wow, det här är en matris” och inser att de kan multiplicera med hjälp av mental matematik, ett uttryck eller en algoritm.

Andra gånger kan eleverna använda visuella modeller för att formulera och lösa problemet.

Hjälp dina elever att hantera utmanande ordproblem

Om du är som många lärare kanske du är orolig för hur dina elever ska hantera allt detta. Processer, strategier, kritiskt tänkande … det är mycket inblandat.

Du kanske till och med tänker att ordproblem verkade lättare före den här artikeln. Om så är fallet ber jag om ursäkt.

Nyckeln är att inte bli överväldigad av att försöka göra allting på en gång. Börja med att lösa ett enkelt ordproblem med hjälp av Polyas process. Introducera sedan en ny strategi varje vecka. I slutet av året kommer du att bli förvånad över hur långt de har kommit.

Kanske är du intresserad av att gå djupare in på kreativ problemlösning. Överväg att delta i en praktisk matematikworkshop eller arbeta med en onlinecoach.

Om du är redo att ta in lite Polya i ditt klassrum imorgon är den här grafiska organisatören ett bra sätt att börja. Den ger stöd för processen i fyra steg och hjälper dig att identifiera var dina elever hamnar på fel spår.

Free Word Problem Organizer

Om författaren

Jeff Lisciandrello är grundare av Room to Discover och utbildningskonsult som specialiserar sig på elevcentrerat lärande. Hans 3-Bridges Design for Learning hjälper skolor att utforska innovativa metoder inom traditionella miljöer. Han tycker om att hjälpa pedagoger att använda undersökningsbaserade och personliga metoder för undervisning. Du kan komma i kontakt med honom via Twitter @EdTechJeff

.