Som en tårta kan du ha två små bitar eller en bit som är dubbelt så stor och det är samma mängd. Därför är många bråk likvärdiga, som 2/5 och 4/10.


Alla tal kan skrivas som en bråkdel
Skriv alla heltal över 1 för att göra det till en bråkdel eftersom det totala antalet delar i en odelad helhet är ett.
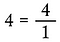
Multiplicera bråk rakt över
Det är enkelt att multiplicera bråk, multiplicera bara rakt över.
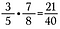
Observera: Blandade tal måste först förvandlas till oäkta bråk, läs mer om detta.
Multiplicera med vilken form av ett som helst
Talet 1 kallas den multiplikativa identiteten eftersom vi kan multiplicera det med vilket tal som helst och talet förblir detsamma. Detta är viktigt för bråk eftersom vi ofta behöver ändra utseendet på ett bråk utan att faktiskt ändra dess värde.
Till exempel kan jag ändra 1/3 till det motsvarande bråket 3/9 genom att multiplicera med 3/3.
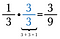
Addera och subtrahera lika stora delar
När vi adderar och subtraherar bråk måste nämnarna vara desamma. Det är logiskt. Om vi vill kombinera eller ta bort delar måste vi prata om delar av samma storlek, annars skulle det bli förvirrande.
Vad gör du då om dina bråk inte har samma storlek?
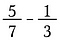
Multiplicera med en form av ett för att ändra nämnarna till en gemensam storlek. I huvudsak delar vi upp bråken i mindre stora bitar tills de är lika stora. Detta kallas att hitta en gemensam nämnare.
Sanningen är att vilken gemensam nämnare som helst duger, men folk föredrar att hitta den minsta. I det här fallet är det minsta talet som både 7 och 3 går in i utan en rest 21. Så multiplicera det första bråket med 3/3 och det andra med 7/7.
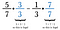
Om du inte kommer på minsta gemensamma nämnare kan du alltid multiplicera varje bråk med den motsatta valören. Ibland, som i det här fallet, visar det sig vara den minsta gemensamma nämnaren. Om det inte är det, minska bara ditt svar på slutet.
När nämnarna stämmer överens subtraherar du täljaren för att få 8/21.
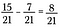
Det här fungerar som man kan förvänta sig. Bildmässigt börjar man med 15 bitar av totalt 21.

För bort färgen från 7 av de 15 blå blocken.

Det ger 8/21 som förväntat.
Skifta ut blandade tal först
Ett blandat tal är kombinationen av ett helt tal och ett bråk.
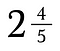
Blandade tal spelar inte bra med andra bråk. Det är en bra idé att först omvandla dem till oäkta bråk.
Notera: Ett oäkta bråk är ett bråk vars täljare är större än dess nämnare och därför har ett värde som är större än ett.
Konvertering av ett blandat tal är egentligen addition
För att omvandla 2 och 4/5 till ett oäkta bråk lägg till 2 + 4/5.
Steg 1: Börja med att skriva om 2 som 2/1.
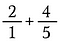
Steg 2: Multiplicera 2/1 med 5/5 för att få fram ett likvärdigt bråk på 10/5 som har den önskade gemensamma nämnaren 5.
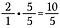
Steg 3: Addera 10/5 + 4/5.
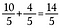
Vårt resultat är det ekvivalenta oäkta bråket 14/5.
För att konvertera tillbaka till ett blandat tal utför du divisionen. Till exempel går 5 in i 14 två gånger (eftersom 5 x 2 = 10) med 4 bitar kvar.
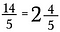
Komparera bråk med hjälp av korsprodukt
Förutsatt att vi vill avgöra vilket som är större: 5/12 eller 6/13.
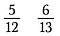
Steg ett: Multiplicera en diagonal och skriv produkten ovanför täljaren.
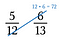
Steg två: Multiplicera den andra diagonalen och skriv produkten över täljaren.
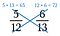
Steg tre: Jämför produkterna. Sidan med den större produkten är det större bråket. Så i det här fallet är 5/12 mindre än 6/13.
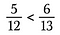
Vi kan avgöra om bråk är lika stora även med hjälp av korsprodukter.
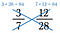
Korsningsprodukten av 3/7 och 12/28 är båda 84, därför är 3/7 = 12/28.
Avbryta allt som dividerar till ett
Det bästa med bråk är att du kan hitta massor av möjligheter att avbryta. Vilket gör dem snabba och enkla att hantera.
Antag att jag har bråket 8/10. Både 8 och 10 kan skrivas om med 2 som faktor.
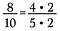
Eftersom 2/2 = 1 kan jag annullera 2:an så att jag får kvar 4/5 som reducerat bråk.
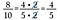
Använd den här strategin för att göra det lättare att multiplicera bråk också.
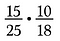
Begynna med att skriva om varje tal i faktorer.
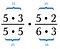
Gör bort alla talpar som delar till 1. Till exempel 5/5 = 1.
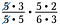
Jag har ytterligare ett par 5:or samt ett par 3:or som också delar till 1.
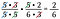
Oj! Jag kunde ha skrivit om 6 som 2 x 3 och strukit ett par 2:or. Det är okej om du missar en faktor, fortsätt bara tills du får fram alla.
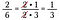
Hade jag multiplicerat 15/25 gånger 10/18 direkt hade det blivit mycket aritmetik, genom att använda annullering förminskar jag bråken i förväg och gör det enklare att multiplicera.
Använd multiplikation för att dela bråk
Begreppet att dela bråk är enkelt med enkla exempel som:

Det finns två halvor i en hel, därför finns det 10 halvor i 5 helheter.
Men begreppet blir knepigt med mer komplicerade bråk.
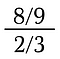
För att lösa det här problemet använder vi oss av två fakta:
- Vi kan multiplicera med alla former av ett (dvs.
- Multiplicera med den reciproka delen av 3/2, som är 2/3, vilket ger 1 via annullering
Steg ett:
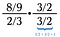
Nu har vi två mindre problem att lösa (blått och grönt).
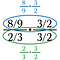
Steg två: Stryk allt som dividerar till 1 i den nedre (gröna) bråkdelen. Detta ska alltid resultera i 1.

Nu återstår det övre problemet att lösa.
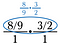
Steg tre: Använd annullering för att minska bråket i förväg. När du har gjort dessa reduktioner multiplicerar du över för att få fram 4/3.

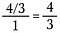
Kortkommandot
Det här är den långa handens mekanik av ”vända och multiplicera”.”
Vi kan hoppa över att multiplicera med reciproken i botten eftersom den alltid upphäver till 1. Därför behöver du bara multiplicera täljaren med reciproken till nämnaren.

Bonus: Teori, om du skulle vara intresserad…
God fråga! För att generalisera, gör två bråk med bokstäverna a, b, c och d för att representera fyra olika tal.
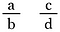
Multiplicera båda bråken med b-d (detta gör det möjligt för oss att upphäva nämnarna).
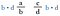
Nu annullerar vi b:et till vänster och d:et till höger eftersom de delar till 1. Vi har inte längre bråk, bara produkterna d-a och c-b.
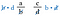
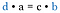
Se tillbaka på de ursprungliga bråken. Det är samma produkter som om vi hade multiplicerat diagonalerna. Därför är genvägen att jämföra korsprodukten.
❤ HÅLL DIG INKOPPLAD ❤
Håll dig uppdaterad om allt som Math Hacks håller på med!