Grafteori – typer av grafer

Det finns olika typer av grafer beroende på antalet hörn, antalet kanter, sammankopplingsmöjligheter och deras övergripande struktur. Vi kommer bara att diskutera några få viktiga typer av grafer i det här kapitlet.

Nollgraf

En graf som inte har några kanter kallas för en nollgraf.

Exempel

I grafen ovan finns det tre hörn med namnen ”a”, ”b” och ”c”, men det finns inga kanter mellan dem. Därför är det en nollgraf.

Trivialgraf

En graf med endast en topp kallas för en trivialgraf.

Exempel

I grafen ovan finns det endast en topp ”a” utan några andra kanter. Därför är det en Trivialgraf.

Non-Directed Graph

En non-directed graph innehåller kanter men kanterna är inte riktade.

Exempel

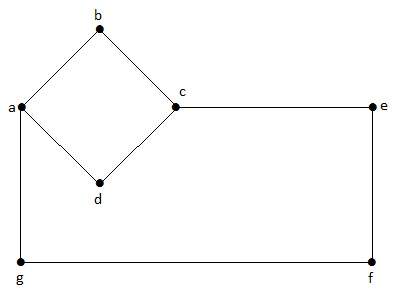
I den här grafen är ”a”, ”b”, ”c”, ”d”, ”e”, ”f”, ”g” hörn och ”ab”, ”bc”, ”cd”, ”da”, ”ag”, ”gf”, ”ef” gravens kanter. Eftersom det är en icke-riktad graf är kanterna ”ab” och ”ba” likadana. På samma sätt betraktas även andra kanter på samma sätt.

Riktad graf

I en riktad graf har varje kant en riktning.

Exempel

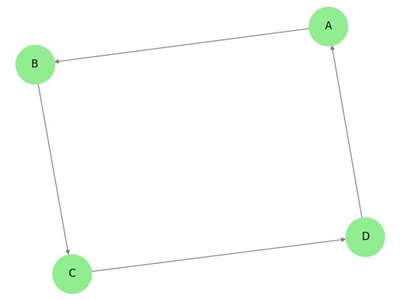
I grafen ovan har vi sju hörn ”a”, ”b”, ”c”, ”d”, ”e”, ”f” och ”g” och åtta kanter ”ab”, ”cb”, ”dc”, ”ad”, ”ec”, ”fe”, ”gf” och ”ga”. Eftersom det är ett riktat diagram är varje kant försedd med en pil som visar dess riktning. Observera att i en riktad graf är ”ab” annorlunda än ”ba”.

En enkel graf

En graf utan slingor och utan parallella kanter kallas för en enkel graf.

• Det maximala antalet kanter som är möjligt i en enkel graf med ”n” hörn är nC2 där nC2 = n(n – 1)/2.

• Antalet möjliga enkla grafer med ’n’ hörn är 2nc2 = 2n(n – 1)/2.

Exempel

I följande graf finns det 3 hörn med 3 kanter vilket är maximalt om man bortser från parallella kanter och slingor. Detta kan bevisas med hjälp av ovanstående formler.

Det maximala antalet kanter med n=3 hörn –

nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges

Det maximala antalet enkla grafer med n=3 hörn –

2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8

Dessa 8 grafer visas nedan –

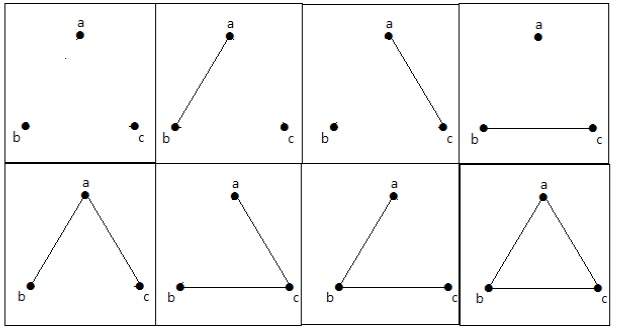
Sammanhängande grafer

En graf G sägs vara sammankopplad om det finns en väg mellan varje par hörn. Det ska finnas minst en kant för varje hörn i grafen. Så att vi kan säga att den är ansluten till någon annan topp på andra sidan av kanten.

Exempel

I följande graf har varje topp en egen kant som är ansluten till en annan kant. Därför är det en sammanhängande graf.

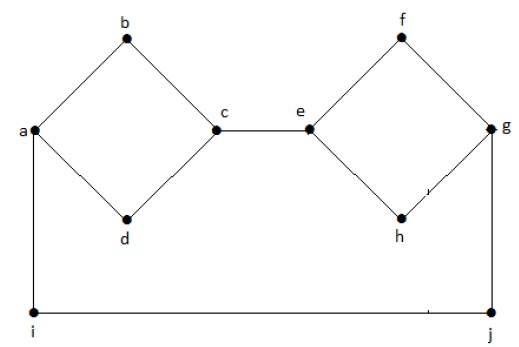
Diskonnekterad graf

En graf G är diskonnekterad om den inte innehåller minst två sammanhängande hörn.

Exempel 1

Den följande grafen är ett exempel på en frånkopplad graf, där det finns två komponenter, en med ”a”, ”b”, ”c”, ”d” hörn och en annan med ”e”, ”f”, ”g”, ”h” hörn.

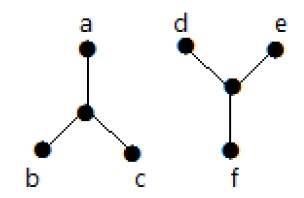
De två komponenterna är oberoende och är inte anslutna till varandra. Därför kallas den för en osammanhängande graf.

Exempel 2

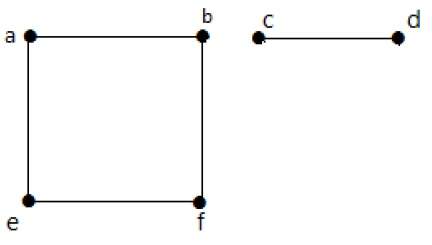
I detta exempel finns det två oberoende komponenter, a-b-f-e och c-d, som inte är sammankopplade med varandra. Därför är detta en osammanhängande graf.

Reguljär graf

En graf G sägs vara reguljär om alla dess hörn har samma grad. Om graden för varje hörn i en graf är ”k” kallas grafen för en ”k-reguljär graf”.

Exempel

I följande grafer har alla hörn samma grad. Så dessa grafer kallas regelbundna grafer.

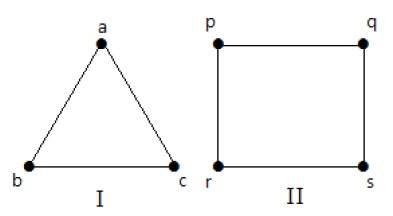
I båda graferna har alla hörn graderna 2. De kallas 2-regulära grafer.

Kompletta grafer

En enkel graf med ”n” ömsesidiga hörn kallas en komplett graf och betecknas med ”Kn”. I grafen ska en topp ha kanter med alla andra toppar, då kallas den en komplett graf.

Med andra ord, om en topp är ansluten till alla andra toppar i en graf kallas den en komplett graf.

Exempel

I följande grafer är varje topp i grafen ansluten till alla övriga toppar i grafen utom till sig själv.

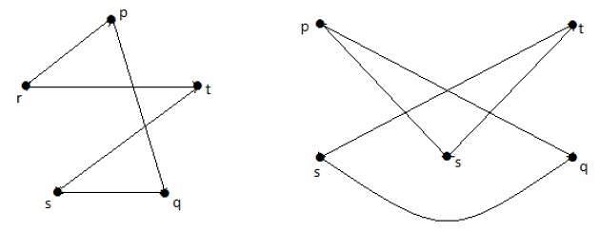
I graf I,

	a	b	c
a	Not Connected	Connected	Connected	Connected
b	Kopplat	Inte kopplat	Kopplat
c	Kopplat	Kopplat	Inte kopplat	Inte kopplat

I diagram II,

	p	q	r	s
p	Inte ansluten	ansluten	ansluten	ansluten	Anslutad
q	Anslutad	Inte ansluten	Anslutad	Anslutad	Anslutad
r	Anslutad	Anslutad	Inte ansluten	Anslutad
s	Anslutad	Anslutad	Anslutad	Inte ansluten	Inte Connected

Cycle Graph

En enkel graf med ”n” hörn (n >= 3) och ”n” kanter kallas en cykelgraf om alla dess kanter bildar en cykel med längden ”n”.

Om graden för varje hörn i grafen är två kallas den en cykelgraf.

Notation – Cn

Exempel

Ta en titt på följande grafer –

• Grafen I har 3 hörn med 3 kanter som bildar en cykel ”ab-bc-ca”.

• Graph II har 4 hörn med 4 kanter som bildar en cykel ’pq-qs-sr-rp’.

• Graph III har 5 hörn med 5 kanter som bildar en cykel ’ik-km-ml-lj-ji’.

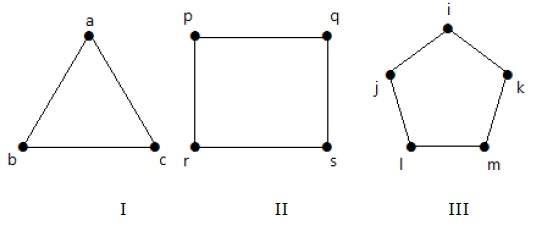
Därmed är alla de givna graferna cykelgrafer.

Hjulgraf

En hjulgraf erhålls från en cykelgraf Cn-1 genom att lägga till en ny hörnpunkt. Den nya vertexen kallas Hub och är ansluten till alla vertexar i Cn.

Notation – Wn

No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)

Exempel

Ta en titt på följande grafer. De är alla hjulgrafer.

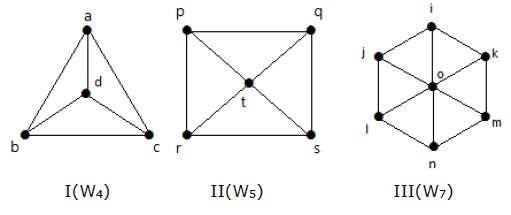
I graf I erhålls den från C3 genom att lägga till en topp i mitten som heter ”d”. Den betecknas W4.

Number of edges in W4 = 2(n-1) = 2(3) = 6

I diagram II erhålls den från C4 genom att lägga till en topp i mitten som heter ”t”. Den betecknas W5.

Number of edges in W5 = 2(n-1) = 2(4) = 8

I diagram III erhålls den från C6 genom att lägga till en topp i mitten med namnet ”o”. Den betecknas som W7.

Number of edges in W4 = 2(n-1) = 2(6) = 12

Cyklisk graf

En graf med minst en cykel kallas en cyklisk graf.

Exempel

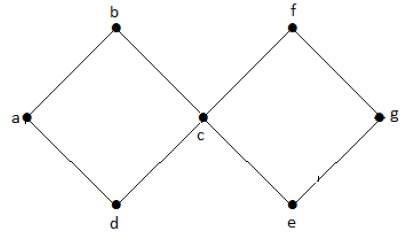
I ovanstående exempelgraf har vi två cykler a-b-c-d-a och c-f-g-e-c. Därför kallas den för en cyklisk graf.

Acyklisk graf

En graf utan cykler kallas för en acyklisk graf.

Exempel

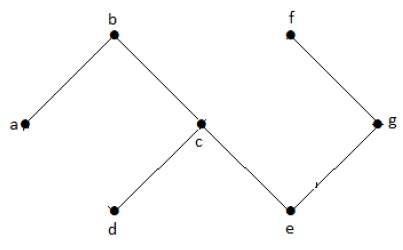
I ovanstående exempelgraf har vi inga cykler. Därför är det en icke-cyklisk graf.

Bipartite Graph

En enkel graf G = (V, E) med toppfördelning V = {V1, V2} kallas en bipartite graf om varje kant i E förenar en topp i V1 med en topp i V2.

En bipartitisk graf har i allmänhet två uppsättningar av hörn, låt oss säga V1 och V2, och om en kant dras ska den förbinda varje hörn i uppsättningen V1 med varje hörn i uppsättningen V2.

Exempel

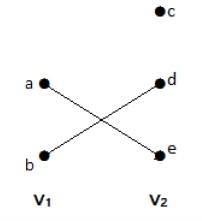
I den här grafen kan man observera två uppsättningar av hörn – V1 och V2. Här finns två kanter som heter ”ae” och ”bd” som förbinder topparna i de två uppsättningarna V1 och V2.

Komplett tvåpartsgraf

En tvåpartsgraf ”G”, G = (V, E) med partitionen V = {V1, V2}, sägs vara en komplett tvåpartsgraf om varje topp i V1 är ansluten till varje topp i V2.

En fullständig tvåpartsgraf förbinder i allmänhet varje topp från mängden V1 med varje topp från mängden V2.

Exempel

Den följande grafen är en fullständig tvåpartsgraf eftersom den har kanter som förbinder varje topp från mängden V1 med varje topp från mängden V2.

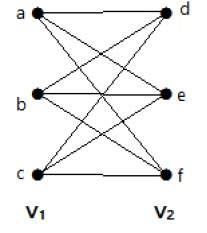
Om |V1| = m och |V2| = n betecknas den fullständiga tvåpartsgrafen med Km, n.

• Km,n har (m+n) hörn och (mn) kanter.

• Km,n är en regelbunden graf om m=n.

En fullständig tvådelad graf är generellt sett inte en fullständig graf.

Km,n är en fullständig graf om m=n=1.

Det maximala antalet kanter i en tvådelad graf med n hörn är

Om n=10, k5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25

Samma sak gäller K6, 4=24

K7, 3=21

K8, 2=16

K9, 1=9

Om n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20

Samma sak med K6, 3=18

K7, 2=14

K8, 1=8

’G’ är en tvådelad graf om ’G’ inte har några cykler av udda längd. Ett specialfall av en tvådelad graf är en stjärngraf.

Stjärngraf

En fullständig tvådelad graf av formen K1, n-1 är en stjärngraf med n noder. En stjärngraf är en komplett tvådelad graf om en enda hörn hör till den ena uppsättningen och alla återstående hörn hör till den andra uppsättningen.

Exempel

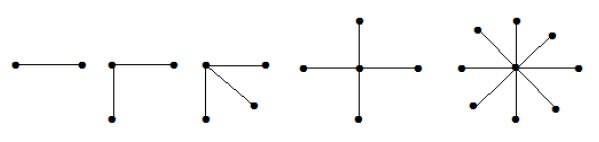
I ovanstående grafer är alla ”n-1” hörn av ”n” hörn anslutna till en enda hörn. Därför är det i form av K1, n-1 som är stjärngrafer.

Komplement till en graf

Låt ”G-” vara en enkel graf med vissa hörn som i ”G” och en kant {U, V} finns i ”G-”, om kanten inte finns i G. Det betyder att två hörn är intilliggande i ”G-” om de två hörnen inte är intilliggande i G.

Om de kanter som finns i graf I saknas i en annan graf II, och om både graf I och graf II kombineras ihop till en komplett graf, kallas graf I och graf II för komplement till varandra.

Exempel

I följande exempel har graf-I två kanter ”cd” och ”bd”. Dess komplement graf-II har fyra kanter.

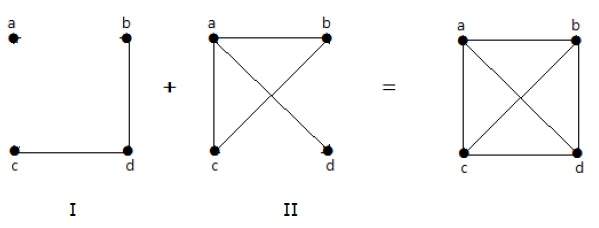
Bemärk att kanterna i graf-I inte finns i graf-II och vice versa. Därför ger kombinationen av båda graferna en komplett graf med ”n” hörn.

Anmärkningar – En kombination av två komplementära grafer ger en komplett graf.

Om ”G” är en enkel graf, då

|E(G)| + |E(’G-’)| = |E(Kn)|, där n = antalet hörn i grafen.

Exempel

Låt ”G” vara en enkel graf med nio hörn och tolv kanter, hitta antalet kanter i ”G-”.

Du får, |E(G)| + |E(’G-’)| = |E(Kn)|

12 + |E(’G-’)| =