Nyligen ställde en kollega till mig några frågor som ”varför har vi så många aktiveringsfunktioner?”, ”varför fungerar den ena bättre än den andra?”, ”hur vet vi vilken funktion vi ska använda?”, ”är det hardcore matematik?” och så vidare. Så jag tänkte, varför inte skriva en artikel om det för dem som är bekanta med neurala nätverk endast på en grundläggande nivå och därför undrar över aktiveringsfunktioner och deras ”varför-hur-matematik!”.
ANMÄRKNING: Den här artikeln förutsätter att du har en grundläggande kunskap om en artificiell ”neuron”. Jag rekommenderar att du läser upp grunderna i neurala nätverk innan du läser den här artikeln för bättre förståelse.
Aktiveringsfunktioner
Så vad gör en artificiell neuron? Enkelt uttryckt beräknar den en ”viktad summa” av sin ingång, lägger till en bias och bestämmer sedan om den ska ”avfyras” eller inte ( javisst, en aktiveringsfunktion gör detta, men låt oss följa med strömmen för ett ögonblick ).
Så tänk på en neuron.
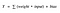
Nu kan värdet på Y vara vad som helst som sträcker sig från -inf till +inf. Neuronen känner egentligen inte till gränserna för värdet. Så hur bestämmer vi om neuronen ska skjuta eller inte ( varför detta skottmönster? Därför att vi har lärt oss det från biologin, det är så hjärnan fungerar och hjärnan är ett fungerande vittnesbörd om ett fantastiskt och intelligent system).
Vi bestämde oss för att lägga till ”aktiveringsfunktioner” för detta ändamål. För att kontrollera det Y-värde som produceras av en neuron och bestämma om externa anslutningar ska betrakta denna neuron som ”avfyrad” eller inte. Eller låt oss snarare säga – ”aktiverad” eller inte.
Stegfunktion
Det första vi tänker på är vad sägs om en tröskelbaserad aktiveringsfunktion? Om värdet på Y ligger över ett visst värde förklarar vi den aktiverad. Om det är lägre än tröskelvärdet, säg att det inte är det. Hmm bra. Detta skulle kunna fungera!
Aktiveringsfunktion A = ”aktiverad” om Y tröskelvärde annars inte
Alternativt, A = 1 om y tröskelvärde, 0 annars
Nja, det vi just gjorde är en ”stegfunktion”, se figuren nedan.
Dess utgång är 1 ( aktiverad) när värdet > 0 (tröskelvärde) och ger ut en 0 ( inte aktiverad) i annat fall.
Snyggt. Detta ger alltså en aktiveringsfunktion för en neuron. Inga förväxlingar. Det finns dock vissa nackdelar med detta. För att förstå det bättre kan du tänka på följande:
Antag att du skapar en binär klassificerare. Något som ska säga ”ja” eller ”nej” ( aktivera eller inte aktivera ). En Step-funktion kan göra det åt dig! Det är precis vad den gör, säger en 1 eller 0. Tänk nu på användningsfallet där du skulle vilja att flera sådana neuroner kopplas samman för att få in fler klasser. Klass1, klass2, klass3 osv. Vad kommer att hända om mer än 1 neuron ”aktiveras”. Alla neuroner kommer att ge ut en 1 (från stegfunktionen). Vad skulle du nu bestämma dig för? Vilken klass är det? Hmm svårt, komplicerat.
Du skulle vilja att nätverket endast aktiverar 1 neuron och att de andra ska vara 0 ( endast då skulle du kunna säga att det klassificerade korrekt/identifierade klassen ). Ah! Det är svårare att träna och konvergera på detta sätt. Det hade varit bättre om aktiveringen inte var binär och det istället skulle stå ”50 % aktiverad” eller ”20 % aktiverad” och så vidare. Och sedan, om mer än 1 neuron aktiveras, skulle man kunna hitta vilken neuron som har den ”högsta aktiveringen” och så vidare ( bättre än max, en softmax, men låt oss lämna det för tillfället ).
Också i det här fallet, om mer än 1 neuron säger ”100 % aktiverad”, kvarstår problemet fortfarande.Jag vet! Men..eftersom det finns mellanliggande aktiveringsvärden för utgången kan inlärningen bli jämnare och enklare ( mindre vinglig ) och chansen att mer än 1 neuron är 100 % aktiverad är mindre jämfört med stegfunktionen under träningen ( också beroende på vad du tränar och data ).
Okej, så vi vill ha något som ger oss mellanliggande ( analoga ) aktiveringsvärden istället för att säga ”aktiverad” eller inte ( binärt ).
Det första vi tänker på skulle vara Linjär funktion.
Linjär funktion
A = cx
En rätlinjig funktion där aktiveringen är proportionell mot inmatningen ( som är den viktade summan från neuron ).
På så sätt ger den ett intervall av aktiveringar, så det är inte binär aktivering. Vi kan definitivt koppla ihop några neuroner och om fler än 1 brinner kan vi ta max ( eller softmax) och besluta utifrån det. Så det är också okej. Vad är då problemet med detta?
Om du är bekant med gradientavstigning för träning skulle du märka att för den här funktionen är derivatan en konstant.
A = cx, derivatan med avseende på x är c. Det betyder att gradienten inte har något samband med X. Det är en konstant gradient och nedstigningen kommer att ske på konstant gradient. Om det finns ett fel i förutsägelsen är förändringarna som görs av back propagation konstanta och inte beroende av förändringen i indata delta(x) !!!
Det här är inte så bra! ( inte alltid, men ha tålamod med mig ). Det finns ett annat problem också. Tänk på anslutna lager. Varje lager aktiveras av en linjär funktion. Denna aktivering går i sin tur in i nästa nivå som input och det andra lagret beräknar viktad summa på denna input och den i sin tur avfyras baserat på en annan linjär aktiveringsfunktion.
Oavsett hur många lager vi har, om alla är linjära till sin natur, är den slutliga aktiveringsfunktionen för det sista lagret inget annat än bara en linjär funktion av input från det första lagret! Gör en paus och tänk på det.
Det betyder att dessa två lager ( eller N lager ) kan ersättas med ett enda lager. Ah! Vi förlorade just möjligheten att stapla lager på detta sätt. Oavsett hur vi staplar är hela nätverket fortfarande likvärdigt med ett enda lager med linjär aktivering ( en kombination av linjära funktioner på ett linjärt sätt är fortfarande en annan linjär funktion ).
Vi kan väl gå vidare?
Sigmoidfunktion
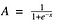
Ja, det här ser ju jämnt ut och ”stegfunktionsliknande”. Vilka är fördelarna med detta? Tänk efter ett ögonblick. Först och främst är det icke-linjärt till sin natur. Kombinationer av denna funktion är också icke-linjära! Bra. Nu kan vi stapla lager på lager. Hur är det med icke-binära aktiveringar? Ja, det också!. Det ger en analog aktivering till skillnad från stegfunktionen. Den har också en jämn gradient.
Och om du märker att mellan X-värdena -2 till 2 är Y-värdena mycket branta. Vilket innebär att varje liten förändring av X-värdena i det området kommer att leda till att Y-värdena förändras avsevärt. Ah, det betyder att den här funktionen har en tendens att föra Y-värdena till endera änden av kurvan.
Det ser ut som om den är bra för en klassificerare med tanke på dess egenskap? Ja ! Det är det verkligen. Den tenderar att föra aktiveringarna till endera sidan av kurvan ( över x = 2 och under x = -2 till exempel). Gör tydliga distinktioner vid prediktion.
En annan fördel med denna aktiveringsfunktion är att till skillnad från linjär funktion kommer aktiveringsfunktionens utgång alltid att ligga i intervallet (0,1) jämfört med (-inf, inf) för linjär funktion. Så vi har våra aktiveringar bundna i ett intervall. Bra, det kommer inte att blåsa upp aktiveringarna då.
Det här är jättebra. Sigmoidfunktioner är en av de mest använda aktiveringsfunktionerna idag. Vilka är då problemen med detta?
Om du märker att mot båda ändarna av den sigmoida funktionen tenderar Y-värdena att reagera mycket mindre på förändringar i X. Vad betyder det? Gradienten i det området kommer att vara liten. Det ger upphov till ett problem med ”försvinnande gradienter”. Hmm. Så vad händer när aktiveringarna når nära den ”nästan horisontella” delen av kurvan på båda sidor?
Gradienten är liten eller har försvunnit ( kan inte göra någon betydande förändring på grund av det extremt lilla värdet ). Nätverket vägrar att lära sig ytterligare eller är drastiskt långsamt ( beroende på användningsfall och tills gradient/beräkning drabbas av gränser för flyttalvärden ). Det finns sätt att arbeta runt detta problem och sigmoid är fortfarande mycket populärt i klassificeringsproblem.
Tanh-funktion
En annan aktiveringsfunktion som används är tanh-funktionen.
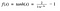
Hm. Detta ser mycket lik ut som sigmoid. Det är faktiskt en skalad sigmoidfunktion!

Okej, nu har detta egenskaper som liknar sigmoid som vi diskuterade ovan. Den är icke-linjär till sin natur, så bra att vi kan stapla lager! Den är bunden till intervallet (-1, 1) så vi behöver inte oroa oss för att aktiveringarna ska sprängas. En sak att nämna är att gradienten är starkare för tanh än för sigmoid (derivatan är brantare). Att välja mellan sigmoid eller tanh beror på ditt krav på gradientstyrka. Liksom sigmoid har tanh också problemet med försvinnande gradient.
Tanh är också en mycket populär och allmänt använd aktiveringsfunktion.
ReLu
Senare kommer ReLu-funktionen,
A(x) = max(0,x)
Relu-funktionen är som visas ovan. Den ger ett utdata x om x är positivt och 0 annars.
Vid en första anblick skulle det se ut som om den har samma problem som den linjära funktionen, eftersom den är linjär i positiv axel. För det första är ReLu icke-linjär till sin natur. Och kombinationer av ReLu är också icke-linjära! ( I själva verket är det en bra approximator. Alla funktioner kan approximeras med kombinationer av ReLu). Bra, det betyder alltså att vi kan stapla lager. Det är dock inte bundet. ReLu har en räckvidd på [0, inf]. Detta innebär att den kan blåsa upp aktiveringen.
En annan punkt som jag skulle vilja diskutera här är aktiveringens gleshet. Tänk dig ett stort neuralt nätverk med många neuroner. Att använda en sigmoid eller tanh kommer att få nästan alla neuroner att starta på ett analogt sätt ( minns du? ). Det innebär att nästan alla aktiveringar kommer att bearbetas för att beskriva utgången av ett nätverk. Med andra ord är aktiveringen tät. Detta är kostsamt. Vi skulle helst vilja att några få neuroner i nätverket inte aktiveras och därmed göra aktiveringarna glesa och effektiva.
ReLu ger oss denna fördel. Föreställ dig ett nätverk med slumpmässigt initialiserade vikter ( eller normaliserade ) och nästan 50 % av nätverket ger 0 aktivering på grund av ReLu:s egenskap ( output 0 för negativa värden på x ). Detta innebär att färre neuroner avfyras ( sparsam aktivering ) och att nätverket är lättare. Woah, trevligt! ReLu verkar vara fantastisk! Ja det är det, men ingenting är felfri… Inte ens ReLu.
På grund av den horisontella linjen i ReLu ( för negativt X ) kan gradienten gå mot 0. För aktiveringar i det området i ReLu kommer gradienten att vara 0, vilket gör att vikterna inte justeras under nedstigningen. Det innebär att de neuroner som går in i detta tillstånd kommer att sluta reagera på variationer i felet/inmatningen ( eftersom gradienten är 0 förändras ingenting ). Detta kallas för döende ReLu-problem. Detta problem kan leda till att flera neuroner bara dör och inte reagerar, vilket gör att en stor del av nätverket blir passivt. Det finns varianter i ReLu för att mildra detta problem genom att helt enkelt göra den horisontella linjen till en icke-horisontell komponent, t.ex. y = 0,01x för x<0, vilket gör den till en något lutande linje i stället för en horisontell linje. Detta är läckande ReLu. Det finns även andra varianter. Huvudidén är att låta gradienten vara icke-noll och återhämta sig under träningen så småningom.
ReLu är mindre beräkningskrävande än tanh och sigmoid eftersom den omfattar enklare matematiska operationer. Det är en bra punkt att tänka på när vi utformar djupa neurala nät.
Okej, vilken ska vi nu använda?
Nu ska vi ta reda på vilka aktiveringsfunktioner vi ska använda. Betyder det att vi bara använder ReLu för allt vi gör? Eller sigmoid eller tanh? Ja och nej. När man vet att den funktion man försöker approximera har vissa egenskaper kan man välja en aktiveringsfunktion som approximerar funktionen snabbare vilket leder till en snabbare träningsprocess. En sigmoid fungerar till exempel bra för en klassificerare (se grafen för sigmoid, visar den inte egenskaperna hos en idealisk klassificerare? ) eftersom det är lättare att approximera en klassificeringsfunktion som kombinationer av en sigmoid än till exempel ReLu. Vilket kommer att leda till snabbare träningsprocess och konvergens. Du kan använda dina egna anpassade funktioner också!. Om du inte vet vilken typ av funktion du försöker lära dig, så kanske jag skulle föreslå att du börjar med ReLu och sedan arbetar bakåt. ReLu fungerar för det mesta som en allmän approximator!
I den här artikeln har jag försökt beskriva några aktiveringsfunktioner som används ofta. Det finns andra aktiveringsfunktioner också, men den allmänna idén förblir densamma. Forskning efter bättre aktiveringsfunktioner pågår fortfarande. Hoppas att du fick idén bakom aktiveringsfunktionen, varför de används och hur vi bestämmer oss för vilken funktion vi ska använda.