 |
 |
| HYDROFOILS | ||
| FRÅGOR ELLER KOMMENTARER | ||
|
|
AUTHOR: | Tina Rosado |
| E-MAIL: | [email protected] | |
| KURS: | 2 | |
| KLASS/ÅR: | 2 | |
HUVUDFUNKTIONSKRAV:
DESIGN PARAMETER: Hydrofoil (Det är en folie eller vinge under vatten som används för att lyfta båtens skrov tills det är helt utanför vattnet.)
GEOMETRI/STRUKTUR:
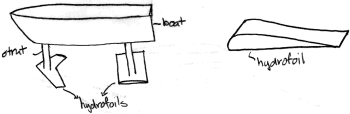
Detaljering av hydrofoils geometri
UTFÖRKLARING AV HUR DET FUNGERAR/ÄR ANVÄNDT:
1. Vid låga hastigheter ligger skrovet (fartygskroppen) i vattnet och bärplanerna är helt nedsänkta i vattnet.
2. När båtens hastighet ökar skapar bärplanerna en lyftkraft.
3. Vid en viss hastighet är den lyftkraft som bärplanerna ger upphov till lika stor som summan av båtens och lastens vikt. Därför kommer skrovet ut ur vattnet.
4. Istället för att ha ett ökat luftmotstånd med ökad hastighet eftersom skrovet lyfts ut ur vattnet (i motsats till vad som händer i traditionella båtar på grund av tryckmotstånd), ger hydrofoilerna ett effektivare sätt att kryssa. Minskat luftmotstånd bidrar till en bättre användning av den kraft som behövs för båtens förflyttning.
DOMINANT FYSIK:
Hur produceras lyftet – Fluiddynamik.
För detta projekt kommer två förklaringar att presenteras på ett allmänt och grundläggande sätt. Dessa teorier är tillämpningen av Bernoullis ekvation och Eulers ekvation för strömlinjekrökningseffekten.
Bernoullis ekvation: Po = P1 + ½
rv1² + rgy1 = P2 + ½rv2² + rgy2
| Variabler | Enheter |
| Po Stagnationstryck | eller |
| P Tryck | eller |
| r Densitet | eller |
| V Hastighet | eller |
| g Gravitationskonstant | eller |
| y Höjd | eller |
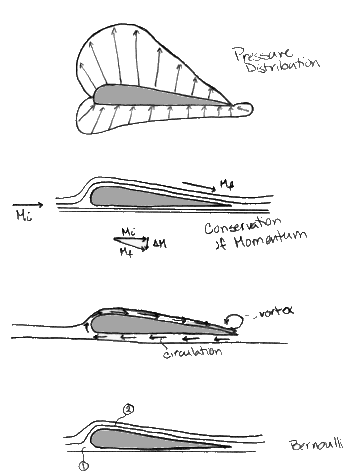
Detalj för bärplansflygplan: a) Tryckprofil b) Momentöverföring c) Cirkulation d) Strömningslinjer
Denna ekvation gäller för flöden längs en strömningslinje som kan modelleras som: inviscida, inkompressibla, stabila, irroterande och för vilka kroppskrafterna är konservativa. Skillnaden i foliernas höjd (avståndet från den nedre sektionen till den övre) är tillräckligt liten för att skillnaden rgy2 – rgy1 skall vara försumbar jämfört med skillnaden i resten av termerna. Det som återstår är att trycket plus halva densiteten gånger hastigheten i kvadrat är lika med en konstant (stagnationstrycket).
När hastigheten längs dessa strömlinjer ökar sjunker trycket (detta kommer att bli viktigt inom kort). Den vätska som rör sig över foliens övre yta rör sig snabbare än den vätska som befinner sig på undersidan. Detta beror delvis på visueffekter som leder till att det bildas virvlar i slutet av folien.För att bevara vinkelmomentet som orsakas av virvlarnas rotation moturs måste det ske ett lika stort men motsatt momentutbyte till virveln vid foliernas bakkant. Detta leder till att vätskan cirkulerar runt folien. Vektorsumman av hastigheterna resulterar i en högre hastighet på den övre ytan och en lägre hastighet på den nedre ytan.Om man tillämpar detta på Bernoullis kan man konstatera att när folien skär genom vätskan ger hastighetsförändringen upphov till det tryckfall som krävs för lyftet. Som det visas i diagrammet är den resulterande eller nettokraften (kraft=(tryck)(area)) uppåt. Denna förklaring kan berikas med principen om momentets bevarande (moment = (massa) (hastighet)). Om hastigheten hos en partikel med ett ursprungligt moment ökas, finns det ett reaktantmoment som är lika stort och motsatt i riktning till skillnaden mellan momenten. (Se diagrammet).(Mi = Mf + DM)
Eulers ekvation: d(p+rgy)/dn = rv²/R
| Variabler | Enheter |
| P Tryck | eller |
| r Densitet | eller |
| V Hastighet | eller |
| g Gravitationskonstant | eller |
| y Höjd | eller |
| n Vektor i radiell riktning | — |
| R Krökningsradie för strömlinje | eller |
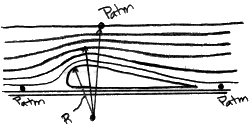
Detalj av trycket i punkter över en flygplansskiva
Här igen, termen som avser höjden antas vara försumbar jämfört med de andra termerna i ekvationen. Denna ekvation säger att trycket på strömlinjerna ökar ju längre bort från centrum av krökningsradien för en strömlinje man kommer. Foljans övre yta ligger närmare centrum för strömlinjerna och därför kommer trycket att vara lägre än det omgivande trycket ovanför folien. Skillnaden mellan trycket på den övre ytan och det omgivande trycket på den nedre ytan ger ett nettotryck som orsakar lyftet (Seediagram.)
Angreppsvinkel:

Angreppsvinkel
Som det har presenterats kommer lyftet från dynamiken hos vätskan i de områden som omger folien. Lyftet kan dock optimeras genom att hydrofoilen placeras i en vinkel (i förhållande till det inkommande vätskeflödet) som kallas angreppsvinkel (se diagrammet). Målet är att optimera förhållandet mellan lyftkraft och luftmotstånd. Detta förhållande beror på formen på folien, som i det här fallet anses vara en tunn folie. Med en liten anfallsvinkel ökar lyftkraften snabbt medan luftmotståndet ökar i liten takt. Efter en vinkel på ~10° ökar lyftet långsamt fram till ~15° där det når sitt maximum. Efter ~15° kan stall uppstå. När anfallsvinkeln är 3° till 4° är förhållandet mellan lyftkraft och luftmotstånd maximalt.Folien är alltså effektivare vid dessa vinklar (3°och 4°) med ett förhållande mellan lyftkraft och luftmotstånd på ~ 20 till 25:1
Begränsande fysik:
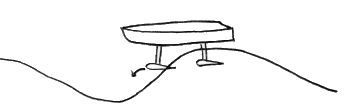
Detaljering av hydrofoliernas geometri
I första hand kan man tänka sig att stallning troligen kommer att vara ett problem i hydrofolier liksom i flygplansprofiler, men förvånansvärt nog är det inte det. En brant anfallsvinkel behövs inte vid utformningen av hydrofoilen. Tvärtom används små angreppsvinklar på hydrofoils för att optimera förhållandet mellan lyftkraft och luftmotstånd, vilket förklarats tidigare.
Vad som är av största vikt är utformningen av folien, stöttorna/stödet och deras placering. Alla dessa egenskaper måste beaktas. Dessa funktioner är alltså utformade för att ge en lägsta hastighet som lyfter båten med en viss vikt och håller den i foil.
Ett problem som en bärplansbåt kan uppleva är att vågornas höjd är större än stöttorna. Om farkosten färdas snabbare än vågorna kan också folierna bryta sig upp till ytan och utanför vattnet, vilket leder till en förlust av lyftkraft och en negativ anfallsvinkel när folien dyker in i nästa våg, vilket gör att farkosten störtar i havet. Ingenjörer har konstruerat hydrofoils för att minimera dessa begränsningar och förbättra fartygets prestanda.
PLOTS/GRAPPER/TABELLER:
Ingen inlämnad
Vissa hydrofoils och deras användning:
Hydrofoils har blivit mycket populära. De används vid olika typer av resor till sjöss, från militär användning till vattensporter. Den höga hastigheten, den jämna färden och de bättre svängar som hydrofoilerna ger har använts i militära fartyg. Segling har också använt hydrofoiler för att få högre hastighet. De möjliggör nya uppfinningar som kan tillfredsställa människors önskan att utmana faran, t.ex. skyski. Det är en vattenskida med en hydrofoil som gör det möjligt för människor att flyga ovanför vattenytan. Varje dag används fler bärplansbåtar, och i framtiden kan de bli den dominerande metoden för resor till sjöss.
REFERENSER/MER INFORMATION:
Se även på den här webbplatsen: Airfoil, Sailboats
Alexander, Alan, James Grogono och Donald Nigg; Hydrofoil Sailing. JuanitaKalerghi: London, 1972.
Bertin, John och Michael Smith; Aerodynamics for Engineers, Third Ediotion.Prentice Hall: New Jersey, 1998.
Hook, Cristopher and A.C. Kermode; Hydrofoils. Pitman Paperbags: London, 1967.
The International Hydrofoil Societys Web Page:http://www.erols.com/foiler/index.html
