Tangentă hiperbolică: Introducere în funcția tangentă hiperbolică

Introducere în funcția tangentă hiperbolică

Definirea funcției tangentă hiperbolică

Funcția tangentă hiperbolică este o funcție matematică veche. Ea a fost utilizată pentru prima dată în lucrarea lui L’Abbe Sauri (1774).

Această funcție este ușor de definit ca fiind raportul dintre funcțiile sinus și cosinus hiperbolice (sau, extins, ca raportul dintre semidiferența și semisuma a două funcții exponențiale în punctele și ):

După compararea cu faimoasele formule ale lui Euler pentru funcțiile sinus și cosinus, și , este ușor de dedus următoarea reprezentare a tangentei hiperbolice prin funcția tangentă circulară:

Această formulă permite derivarea tuturor proprietăților și formulelor pentru tangenta hiperbolică din proprietățile și formulele corespunzătoare pentru tangenta circulară.

O privire rapidă asupra funcției tangentă hiperbolică

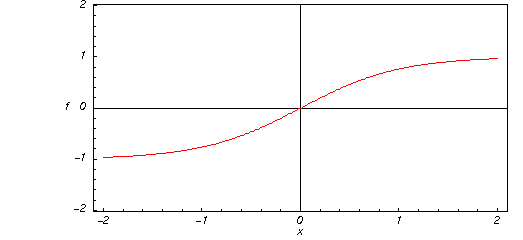
Iată un grafic al funcției tangentă hiperbolică pentru valori reale ale argumentului său .

Reprezentare prin funcții mai generale

Funcția tangentă hiperbolică poate fi reprezentată cu ajutorul unor funcții matematice mai generale. Ca raport al funcțiilor sinus și cosinus hiperbolice care sunt cazuri particulare ale funcțiilor hipergeometrice generalizate, Bessel, Struve și Mathieu, funcția tangentă hiperbolică poate fi reprezentată, de asemenea, ca raport al acestor funcții speciale. Dar aceste reprezentări nu sunt foarte utile. Este mai utilă scrierea funcției tangente hiperbolice ca cazuri particulare ale unei funcții speciale. Acest lucru se poate face folosind funcții eliptice Jacobi dublu periodice care degenerează în funcția tangentă hiperbolică atunci când al doilea parametru al acestora este egal cu sau :

Definirea funcției tangentă hiperbolică pentru un argument complex

În planul complex , funcția se definește prin aceeași formulă care se folosește pentru valorile reale:

În punctele , unde are zerouri, numitorul ultimei formule este egal cu zero, iar are singularități (poli de ordinul întâi).

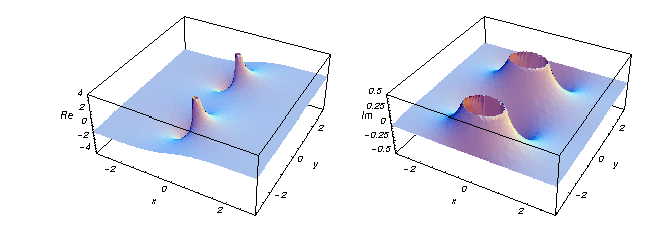
Iată două grafice care prezintă părțile reale și imaginare ale funcției tangente hiperbolice pe planul complex.

Cele mai cunoscute proprietăți și formule pentru funcția tangentă hiperbolică

Valorile în puncte

Valorile tangentei hiperbolice pentru valori speciale ale argumentului său pot fi ușor derivate din valorile corespunzătoare ale tangentei circulare în punctele speciale ale cercului:

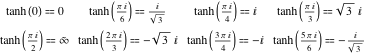
Valorile la infinit pot fi exprimate prin următoarele formule:

Caracteristici generale

Pentru valori reale ale argumentului , valorile lui sunt reale.

În punctele , valorile lui sunt algebrice. În mai multe cazuri, ele pot fi , 0 sau ⅈ:

Valorile lui pot fi exprimate folosind numai rădăcini pătrate dacă și este un produs al unei puteri a lui 2 și al unor numere prime Fermat distincte {3, 5, 17, 257, …}.

Funcția este o funcție analitică a lui care este definită pe întregul plan complex -plan și nu are tăieturi și puncte de ramificare. Ea are un set infinit de puncte singulare:

(a) sunt polii simpli cu resturile 1. (b) este un punct singular esențial.

Este o funcție periodică cu perioada :

Funcția este o funcție impară cu simetrie în oglindă:

Diferențiere

Derivata întâi a lui are reprezentări simple folosind fie funcția , fie funcția :

Derivata a lui are reprezentări mult mai complicate decât derivatele simbolice pentru și :

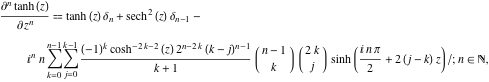
unde este simbolul delta Kronecker: și .

Ecuația diferențială ordinară

Funcția satisface următoarea ecuație diferențială neliniară de ordinul întâi:

Reprezentare în serie

Funcția are o expansiune în serie simplă la origine care converge pentru toate valorile finite cu :

unde sunt numerele lui Bernoulli.

Reprezentare integrală

Funcția are o binecunoscută reprezentare integrală prin următoarea integrală definită de-a lungul părții pozitive a axei reale:

Reprezentări de fracții continue

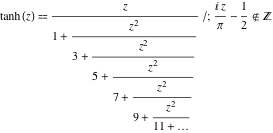
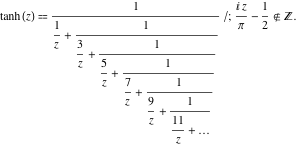
Funcția are următoarele reprezentări simple de fracții continue:

Integrare nedefinită

Integralele nedefinite ale expresiilor care implică funcția tangentă hiperbolică pot fi exprimate uneori folosind funcții elementare. Cu toate acestea, sunt necesare frecvent funcții speciale pentru a exprima rezultatele chiar și atunci când integranții au o formă simplă (dacă pot fi evaluați în formă închisă). Iată câteva exemple:

Integrare definitivă

Integralele definite care conțin funcția tangentă hiperbolică sunt uneori simple. De exemplu, faimoasa constantă catalană poate fi definită prin următoarea integrală:

Câteva funcții speciale pot fi folosite pentru a evalua integrale definite mai complicate. De exemplu, funcția hipergeometrică este necesară pentru a exprima următoarea integrală:

Suma finită

Suma finită următoare, care conține funcția tangentă hiperbolică, poate fi exprimată cu ajutorul funcțiilor cotangente hiperbolice:

Formule de adunare

Tangenta hiperbolică a unei sume poate fi reprezentată prin regula: „tangenta hiperbolică a unei sume este egală cu suma tangentelor hiperbolice împărțită la unu plus produsul tangentelor hiperbolice”. O regulă similară este valabilă pentru tangenta hiperbolică a diferenței:

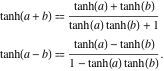
Argumente multiple

În cazul argumentelor multiple , , …, funcția poate fi reprezentată ca raport al sumelor finite care include puteri ale tangentelor hiperbolice:

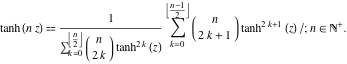
Formulele semicercului

Tangenta hiperbolică a unui semicerc poate fi reprezentată cu ajutorul a două funcții hiperbolice prin următoarele formule simple:

Tangenta hiperbolică a unui semicerc:

Funcția sinus hiperbolică din ultima formulă poate fi înlocuită cu funcția cosinus hiperbolică. Dar aceasta conduce la o reprezentare mai complicată care este valabilă într-o bandă orizontală:

Ultimele restricții pot fi eliminate prin modificarea ușoară a formulei (acum identitatea este valabilă pentru toate complexele ):

Sumele a două funcții directe

Suma a două funcții tangente hiperbolice poate fi descrisă prin regula: „suma tangentelor hiperbolice este egală cu sinusul hiperbolic al sumei înmulțit cu secantele hiperbolice”. O regulă similară este valabilă pentru diferența a două tangente hiperbolice:

Produsele care implică funcția directă

Produsul a două funcții tangente hiperbolice și produsul dintre tangenta hiperbolică și cotangenta hiperbolică au următoarele reprezentări:

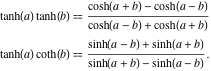
Inegalități

Cea mai cunoscută inegalitate pentru funcția tangentă hiperbolică este următoarea:

Relații cu funcția sa inversă

Există relații simple între funcția și funcția sa inversă :

Cea de-a doua formulă este valabilă cel puțin în banda orizontală . În afara acestei benzi este valabilă o relație mult mai complicată (care conține pasul unitar, partea reală și funcțiile podea):