Styczna hiperboliczna: Wprowadzenie do funkcji stycznej hiperbolicznej

Wprowadzenie do funkcji stycznej hiperbolicznej

Definiowanie funkcji stycznej hiperbolicznej

Funkcja styczna hiperboliczna jest starą funkcją matematyczną. Po raz pierwszy została użyta w pracy L’Abbe Sauri (1774).

Funkcję tę można łatwo zdefiniować jako stosunek sinusa hiperbolicznego i cosinusa hiperbolicznego (lub rozwinąć, jako stosunek półróżnicy i półsumy dwóch funkcji wykładniczych w punktach i ):

Po porównaniu ze słynnymi wzorami Eulera na funkcje sinus i cosinus, i , łatwo wyprowadzić następujące przedstawienie tangensa hiperbolicznego przez funkcję tangensa kołowego:

Wzór ten pozwala wyprowadzić wszystkie własności i wzory dla tangensa hiperbolicznego z odpowiednich własności i wzorów dla tangensa kołowego.

Szybkie spojrzenie na funkcję tangensa hiperbolicznego

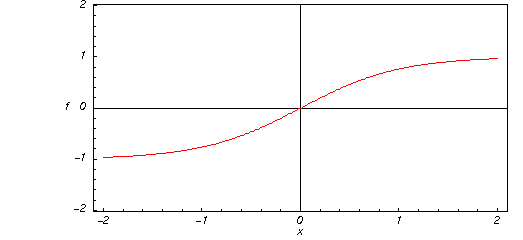
Tutaj znajduje się grafika funkcji tangensa hiperbolicznego dla rzeczywistych wartości jej argumentu .

Reprezentacja za pomocą bardziej ogólnych funkcji

Funkcję tangensa hiperbolicznego można reprezentować za pomocą bardziej ogólnych funkcji matematycznych. Jako stosunek hiperbolicznych funkcji sinus i cosinus, które są szczególnymi przypadkami uogólnionych funkcji hipergeometrycznych, Bessela, Struvego i Mathieu, hiperboliczna funkcja tangensa może być również reprezentowana jako stosunek tych specjalnych funkcji. Ale te reprezentacje nie są zbyt użyteczne. Bardziej użyteczne jest zapisanie hiperbolicznej funkcji stycznej jako szczególnych przypadków jednej funkcji specjalnej. Można to zrobić za pomocą podwójnie okresowych funkcji eliptycznych Jacobiego, które degenerują się do hiperbolicznej funkcji stycznej, gdy ich drugi parametr jest równy lub :

Definicja hiperbolicznej funkcji stycznej dla argumentu złożonego

W płaszczyźnie zespolonej funkcja jest zdefiniowana tym samym wzorem, który jest używany dla wartości rzeczywistych:

W punktach , gdzie ma zera, mianownik ostatniego wzoru równa się zeru, a ma osobliwości (bieguny pierwszego rzędu).

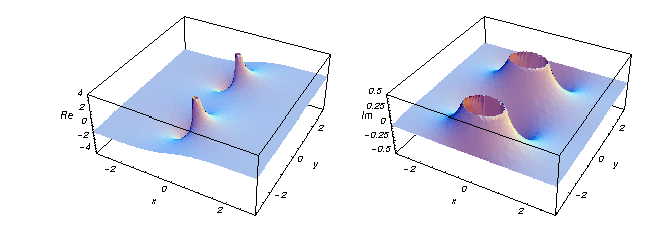
Oto dwie grafiki przedstawiające rzeczywistą i urojoną część hiperbolicznej funkcji stycznej na płaszczyźnie zespolonej.

Najbardziej znane własności i wzory funkcji tangensa hiperbolicznego

Wartości w punktach

Wartości tangensa hiperbolicznego dla szczególnych wartości jego argumentu można łatwo wyprowadzić z odpowiednich wartości tangensa kołowego w szczególnych punktach okręgu:

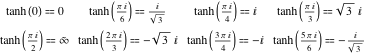
Wartości w nieskończoności można wyrazić następującymi wzorami:

Ogólna charakterystyka

Dla rzeczywistych wartości argumentu , wartości są rzeczywiste.

W punktach , wartości są algebraiczne. W kilku przypadkach mogą być , 0, lub ⅈ:

Wartości można wyrazić za pomocą wyłącznie pierwiastków kwadratowych, jeśli i jest iloczynem potęgi 2 i różnych liczb pierwszych Fermata {3, 5, 17, 257, …}.

Funkcja jest funkcją analityczną , która jest określona na całej złożonej płaszczyźnie i nie ma cięć gałęziowych i punktów gałęziowych. Ma ona nieskończony zbiór punktów osobliwych:

(a) są prostymi biegunowymi o residuach 1.(b) jest istotnym punktem osobliwym.

Jest to funkcja okresowa o okresie :

Funkcja jest funkcją nieparzystą o symetrii lustrzanej:

Różniczkowanie

Pierwsza pochodna ma proste odwzorowania za pomocą funkcji lub funkcji :

Pochodna funkcji ma znacznie bardziej skomplikowane reprezentacje niż symboliczne pochodne dla i :

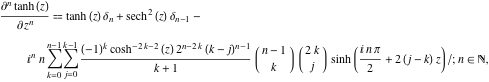
gdzie jest symbolem delty Kroneckera: i .

Równanie różniczkowe zwyczajne

Funkcja spełnia następujące równanie różniczkowe nieliniowe pierwszego rzędu:

Przedstawienie szeregowe

Funkcja ma proste rozwinięcie szeregowe na początku, które jest zbieżne dla wszystkich skończonych wartości z :

gdzie są liczbami Bernoulliego.

Reprezentacja całkowa

Funkcja ma dobrze znaną reprezentację całkową poprzez następującą całkę definitywną wzdłuż dodatniej części osi rzeczywistej:

Reprezentacje ułamka ciągłego

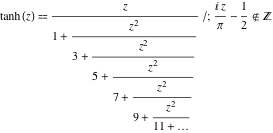
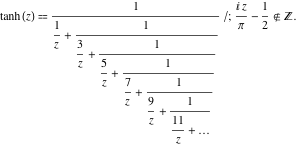
Funkcja ma następujące reprezentacje ułamka zwykłego ciągłego:

Całkowanie nieokreślone

Całki nieokreślone wyrażeń zawierających funkcję tangensa hiperbolicznego można czasem wyrazić za pomocą funkcji elementarnych. Często jednak do wyrażenia wyników potrzebne są specjalne funkcje, nawet gdy całki mają prostą postać (jeśli można je obliczyć w postaci zamkniętej). Oto kilka przykładów:

Całki definitywne

Całki definitywne, które zawierają hiperboliczną funkcję styczną, są czasami proste. Na przykład słynna stała katalońska może być zdefiniowana przez następującą całkę:

Niektóre specjalne funkcje mogą być użyte do oceny bardziej skomplikowanych całek definitywnych. Na przykład, funkcja hipergeometryczna jest potrzebna do wyrażenia następującej całki:

Suma skończona

Następująca suma skończona, która zawiera hiperboliczną funkcję styczną, może być wyrażona za pomocą hiperbolicznych funkcji kotangensa:

Formuły dodawania

Tangens hiperboliczny sumy można przedstawić za pomocą reguły: „tangens hiperboliczny sumy jest równy sumie tangensów hiperbolicznych podzielonej przez jeden plus iloczyn tangensów hiperbolicznych”. Podobna reguła obowiązuje dla tangensa hiperbolicznego różnicy:

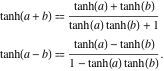
Wielokrotne argumenty

W przypadku wielokrotnych argumentów , , …, funkcję można przedstawić jako iloraz sum skończonych zawierający potęgi tangensów hiperbolicznych:

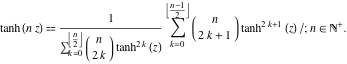
Wzory na półkąty

Styczną hiperboliczną półkąta można przedstawić za pomocą dwóch funkcji hiperbolicznych za pomocą następujących prostych wzorów:

Funkcję sinus hiperboliczny w ostatnim wzorze można zastąpić funkcją cosinus hiperboliczny. Prowadzi to jednak do bardziej skomplikowanej reprezentacji, która obowiązuje w pasie poziomym:

Ostatnie ograniczenia można usunąć modyfikując nieco wzór (teraz tożsamość jest ważna dla wszystkich złożonych ):

Sumy dwóch funkcji bezpośrednich

Suma dwóch funkcji stycznych hiperbolicznych może być opisana regułą: „suma tangensów hiperbolicznych jest równa sinusowi hiperbolicznemu sumy pomnożonemu przez sekanty hiperboliczne”. Podobna reguła obowiązuje dla różnicy dwóch tangensów hiperbolicznych:

Iloczyny z udziałem funkcji bezpośredniej

Iloczyn dwóch tangensów hiperbolicznych oraz iloczyn tangensa hiperbolicznego i cotangensa mają następujące przedstawienia:

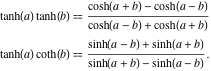
Nierówności

Najsłynniejsza nierówność dla hiperbolicznej funkcji stycznej jest następująca:

Relacje z jej funkcją odwrotną

Pomiędzy funkcją a jej funkcją odwrotną zachodzą proste relacje:

Drugi wzór obowiązuje przynajmniej w poziomym pasie . Poza tym pasem zachodzi znacznie bardziej skomplikowana zależność (zawierająca funkcje stopnia jednostkowego, części rzeczywistej i podłogi):