ハイパーボリックタンジェント関数入門
ハイパーボリックタンジェント関数の定義
ハイパーボリックタンジェント関数は古い数学の関数です。 L’Abbe Sauri (1774)の著作で初めて使われた。
この関数はハイパーボリックサインとコサイン関数の比として簡単に定義できる（あるいは、点
と
における2つの指数関数の半差と半和の比として展開される）。
正弦関数と余弦関数の有名なオイラー公式
と
と比較すると、円接関数による双曲正接は次のように簡単に導出されます。
この式により、双曲線正接のすべての性質と公式が、対応する円形正接の性質と公式から導出されることになる。
双曲線正接関数の早見表
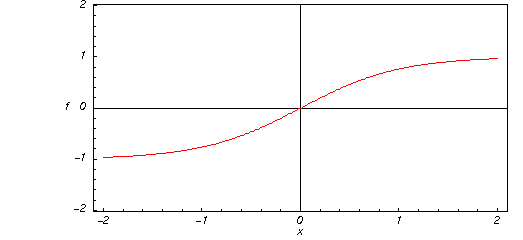
ここで、引数
の実数値に対する双曲線正接関数
の図を示します。
もっと一般的な関数による表現
双曲線正接関数
はもっと一般の数学関数を使って表すことができるのです。 一般化された双曲線関数、ベッセル関数、シュトルーブ関数、マチュー関数の特殊例である双曲線サイン関数とコサイン関数の比として、双曲線正接関数もこれらの特殊関数の比として表すことができます。 しかし、これらの表現はあまり便利ではない。 それよりも、双曲線上の接線関数を、ある特殊な関数の特殊な場合として書く方が便利です。 これは、二重周期のヤコビ楕円関数で、第2パラメータが
か
に等しいときに双曲正接関数に縮退するものを使えばよいのです。
複素引数の双曲線正接関数の定義
複素
平面では、関数
は実数値に使うのと同じ公式で定義されます。
が0を持つ点
では最後の式の分母が0になり
が特異点（一次の極）を持つ。
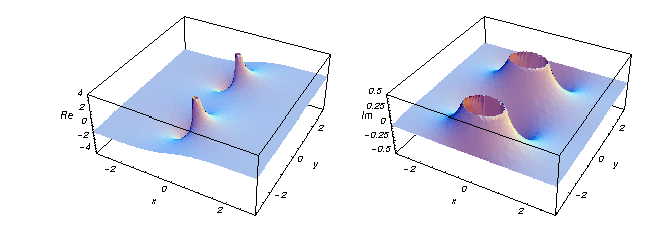
複素平面上の双曲線正接関数の実部、虚部を示す2つの図形を紹介します。
双曲線正接関数の最もよく知られた性質と公式
点における値
その引数の特別な値に対する双曲線接線の値は、円の特殊点における対応する接線の値から簡単に導き出すことができる。
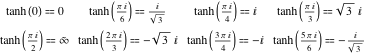
無限での値は次の式で表すことができる。
一般特性
引数
の実数値に対して、
の値は実数値である。
点
では、
の値は代数的である。 いくつかの場合、それらは
、0、またはⅈになる：
と
が2のべき乗と異なるフェルマー素数{3、5、17、257、・・}の積なら、
の値は平方根だけを使って表すことができる。
関数
は
の解析関数で、複素
平面全体にわたって定義され、枝切りと枝点を持たない。
(a)
は残基1を持つ単純極、(b)
は本質的特異点であり、特異点の集合は無限大である。
周期
の周期関数である:
関数
はミラー対称の奇関数である:
周期関数である:
周期関数である。
微分
の1次微分は
関数か
関数を使った簡単な表現があります。
の 
微分は 
や 
の 
微分よりずっと複雑です：
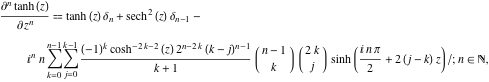
ここで 
はクロネッカーデルタのシンボルです。 
と 
です。
常微分方程式
関数
は次の一階非線形微分方程式を満足する。
直列表現
関数
は、すべての有限値
に対して
:
ここに
はベルヌーイ数で収束する原点の単純級数展開を持っています。
積分表現
関数
は実軸の正の部分に沿った次の定積分によってよく知られた積分表現を持っている：
継続分数表現
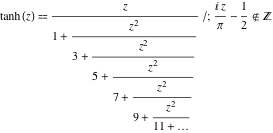
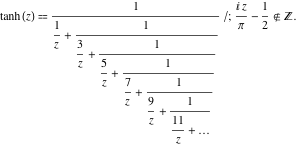
関数
は次の単純な継続分数表現をもっている。
不定積分
双曲接関数を含む式の不定積分は初等関数を使って表現できる場合があります。 しかし、積分が簡単な形であっても（閉形式で評価できる場合）、その結果を表すために特殊な関数が必要になることがよくあります。 以下はその例です。
定積分
双曲接線関数が入った定積分も単純であったりするわけですが、この定積分も単純であったりします。 例えば、有名なカタラン定数 
は次の積分で定義できます：
いくつかの特殊な関数は、より複雑な定積分を評価するために使用することができます。 例えば、次の積分を表すには超幾何関数が必要です：
有限和
双曲接関数を含む次の有限和は双曲共接関数を使って表すことができます。
加算式
和の双曲線正接は、「和の双曲線正接は、双曲線正接の積を1で割ったものと同じ」という規則で表現することができる。 同様の規則が差の双曲線正接にも成り立つ。
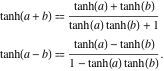
複数の引数
の場合、関数
は双曲線正接のべき乗を含む有限和の比として表すことができる。
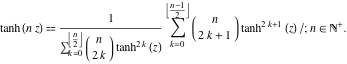
半角の公式
＜4420＞半角の双曲接は二つの双曲関数を使って次の簡単な公式で表せます。
最後の式の双曲線サイン関数は双曲線余弦関数に置き換えることができる。 しかし、それは横縞で有効な、より複雑な表現になる：
最後の制限は、式を少し修正することで取り除くことができる（これで恒等式はすべての複素数
に対して有効である）。
二つの直接関数の和
二つの双曲正接関数の和は次の規則で記述できる： 「双曲正接の和は和の双曲正弦に双曲分線をかけたものと同じである」。 同様の規則が2つの双曲線正接の差にも当てはまる：
直接関数を含む積
2つの双曲線正接関数の積、双曲線正接と共接の積は次の表現になる。
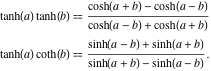
不等式
双曲正接関数の最も有名な不等式は次の通りである。
その逆関数との関係
関数
とその逆関数
との間には簡単な関係がある。
この2番目の式は少なくとも横縞
の中で有効である。 この帯の外ではもっと複雑な関係(単位ステップ、実部、階関数を含む)が成り立つ。
他の双曲関数による表現
双曲正接関数と副接点は、引数に線形関数を含む非常に簡単な公式で接続されています。
双曲正接関数は、他の双曲関数を通しても、次の式で表すことができる。
三角関数による表現
双曲接線関数には、三角関数を使った表現があります。
応用
双曲正接関数は数学、正確科学、工学で使用されています。