Introduzione alla funzione tangente iperbolica
Definizione della funzione tangente iperbolica
La funzione tangente iperbolica è una vecchia funzione matematica. Fu usata per la prima volta nell’opera di L’Abbe Sauri (1774).
Questa funzione è facilmente definibile come il rapporto tra le funzioni seno e coseno iperboliche (o espanso, come il rapporto tra la semidifferenza e la semisomma di due funzioni esponenziali nei punti 
e 
):
Dopo il confronto con le famose formule di Eulero per le funzioni seno e coseno, 
e 
, è facile ricavare la seguente rappresentazione della tangente iperbolica attraverso la funzione tangente circolare:
Questa formula permette di derivare tutte le proprietà e formule della tangente iperbolica dalle corrispondenti proprietà e formule della tangente circolare.
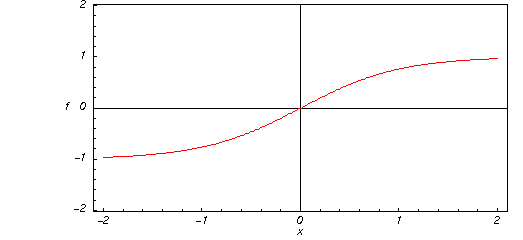
Un rapido sguardo alla funzione tangente iperbolica
Ecco un grafico della funzione tangente iperbolica 
per valori reali del suo argomento 
.
Rappresentazione attraverso funzioni più generali
La funzione tangente iperbolica 
può essere rappresentata utilizzando funzioni matematiche più generali. Come il rapporto delle funzioni seno e coseno iperboliche che sono casi particolari delle funzioni ipergeometriche generalizzate, Bessel, Struve e Mathieu, la funzione tangente iperbolica può anche essere rappresentata come rapporti di queste funzioni speciali. Ma queste rappresentazioni non sono molto utili. È più utile scrivere la funzione tangente iperbolica come casi particolari di una funzione speciale. Questo può essere fatto usando funzioni ellittiche Jacobi doppiamente periodiche che degenerano nella funzione tangente iperbolica quando il loro secondo parametro è uguale a 
o 
:
Definizione della funzione tangente iperbolica per un argomento complesso
Nel piano complesso 
, la funzione 
è definita dalla stessa formula che si usa per i valori reali:
Nei punti 
, dove 
ha degli zeri, il denominatore dell’ultima formula è uguale a zero e 
ha delle singolarità (poli del primo ordine).
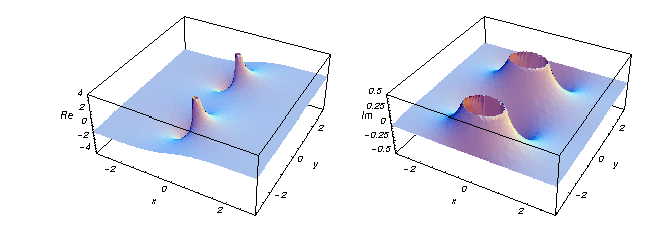
Ecco due grafici che mostrano le parti reali e immaginarie della funzione tangente iperbolica sul piano complesso.
Le proprietà e le formule più note per la funzione tangente iperbolica
Valori in punti
I valori della tangente iperbolica per particolari valori del suo argomento possono essere facilmente derivati dai corrispondenti valori della tangente circolare nei particolari punti del cerchio:
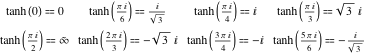
I valori all’infinito possono essere espressi dalle seguenti formule:
Caratteristiche generali
Per valori reali dell’argomento 
, i valori di 
sono reali.
Nei punti 
, i valori di 
sono algebrici. In diversi casi, possono essere 
, 0, o ⅈ:
I valori di 
possono essere espressi usando solo radici quadrate se 
e 
è un prodotto di una potenza di 2 e di distinti primi di Fermat {3, 5, 17, 257, …}.
La funzione 
è una funzione analitica di 
che è definita su tutto il piano complesso 
e non ha tagli e punti di ramo. Ha un insieme infinito di punti singolari:
(a) 
sono i poli semplici con residui 1.(b) 
è un punto singolare essenziale.
È una funzione periodica con periodo 
:
La funzione 
è una funzione dispari con simmetria speculare:
Differenziazione
La derivata prima di 
ha rappresentazioni semplici usando o la funzione 
o la funzione 
:
La derivata 
di 
ha rappresentazioni molto più complicate delle derivate simboliche 
per 
e 
:
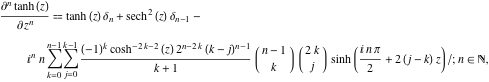
dove 
è il simbolo delta di Kronecker: 
e 
.
Equazione differenziale ordinaria
La funzione 
soddisfa la seguente equazione differenziale non lineare del primo ordine:
Rappresentazione in serie
La funzione 
ha una semplice espansione in serie nell’origine che converge per tutti i valori finiti 
con 
:
dove 
sono i numeri di Bernoulli.
Rappresentazione integrale
La funzione 
ha una nota rappresentazione integrale attraverso il seguente integrale definito lungo la parte positiva dell’asse reale:
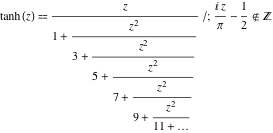
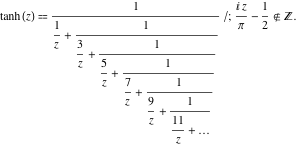
Rappresentazioni di frazioni continue
La funzione 
ha le seguenti rappresentazioni di frazioni continue semplici:
Integrazione indefinita
Integrali indefiniti di espressioni che coinvolgono la funzione tangente iperbolica possono talvolta essere espressi usando funzioni elementari. Tuttavia, sono spesso necessarie funzioni speciali per esprimere i risultati anche quando gli integrali hanno una forma semplice (se possono essere valutati in forma chiusa). Ecco alcuni esempi:
Integrazione definita
Integrali indefiniti che contengono la funzione tangente iperbolica sono talvolta semplici. Per esempio, la famosa costante catalana 
può essere definita attraverso il seguente integrale:
Alcune funzioni speciali possono essere usate per valutare integrali definiti più complicati. Per esempio, la funzione ipergeometrica è necessaria per esprimere il seguente integrale:
Somma finita
La seguente somma finita che contiene la funzione tangente iperbolica può essere espressa usando funzioni cotangenti iperboliche:
Formule di addizione
La tangente iperbolica di una somma può essere rappresentata dalla regola: “la tangente iperbolica di una somma è uguale alla somma delle tangenti iperboliche divisa per uno più il prodotto delle tangenti iperboliche”. Una regola simile è valida per la tangente iperbolica della differenza:
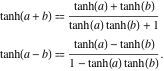
Argomenti multipli
Nel caso di argomenti multipli 
, 
, …, la funzione 
può essere rappresentata come il rapporto delle somme finite che include potenze di tangenti iperboliche:
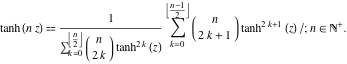
Formule dei semiangoli
La tangente iperbolica di un semiangolo può essere rappresentata utilizzando due funzioni iperboliche con le seguenti semplici formule:
La funzione seno iperbolico nell’ultima formula può essere sostituita dalla funzione coseno iperbolico. Ma questo porta ad una rappresentazione più complicata che è valida in una striscia orizzontale:
Le ultime restrizioni possono essere eliminate modificando leggermente la formula (ora l’identità è valida per tutti i complessi 
):
Somme di due funzioni dirette
La somma di due funzioni tangenti iperboliche può essere descritta dalla regola: “la somma delle tangenti iperboliche è uguale al seno iperbolico della somma moltiplicato per le secanti iperboliche”. Una regola simile è valida per la differenza di due tangenti iperboliche:
Prodotti che coinvolgono la funzione diretta
Il prodotto di due funzioni tangenti iperboliche e il prodotto della tangente e della cotangente iperbolica hanno le seguenti rappresentazioni:
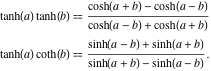
Disuguaglianze
La disuguaglianza più famosa per la funzione tangente iperbolica è la seguente:
Relazioni con la sua funzione inversa
Ci sono semplici relazioni tra la funzione 
e la sua funzione inversa 
:
La seconda formula è valida almeno nella striscia orizzontale 
. Al di fuori di questa striscia vale una relazione molto più complicata (che contiene il passo unitario, la parte reale e le funzioni di piano):
Rappresentazioni attraverso altre funzioni iperboliche
Le funzioni iperboliche tangente e cotangente sono collegate da una formula molto semplice che contiene la funzione lineare nell’argomento:
La funzione tangente iperbolica può anche essere rappresentata attraverso altre funzioni iperboliche dalle seguenti formule:
Rappresentazioni tramite funzioni trigonometriche
La funzione tangente iperbolica ha rappresentazioni che utilizzano le funzioni trigonometriche:
Applicazioni
La funzione tangente iperbolica è usata in tutta la matematica, le scienze esatte e l’ingegneria.