Bevezetés a hiperbolikus érintőfüggvénybe
A hiperbolikus érintőfüggvény meghatározása
A hiperbolikus érintőfüggvény egy régi matematikai függvény. Először L’Abbe Sauri (1774) munkájában használták.
Ezt a függvényt könnyen definiálhatjuk a hiperbolikus szinusz és a koszinusz függvények hányadosaként (vagy kiterjesztve, a ![]() és
és ![]() pontokban két exponenciális függvény fél-különbségének és félösszegének hányadosaként):
pontokban két exponenciális függvény fél-különbségének és félösszegének hányadosaként):
![]()
![]()
A szinusz- és koszinuszfüggvények híres Euler-formuláival ![]() és
és ![]() való összehasonlítás után könnyen levezethető a hiperbolikus érintő következő ábrázolása a körkörös érintőfüggvényen keresztül:
való összehasonlítás után könnyen levezethető a hiperbolikus érintő következő ábrázolása a körkörös érintőfüggvényen keresztül:
![]()
![]()
Ez a képlet lehetővé teszi a hiperbolikus érintő összes tulajdonságának és képletének levezetését a körkörös érintő megfelelő tulajdonságaiból és képleteiből.
Egy gyors pillantás a hiperbolikus érintőfüggvényre
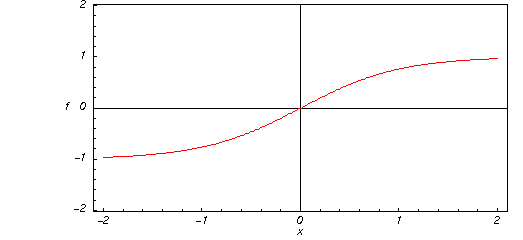
Itt a hiperbolikus érintőfüggvény ![]() grafikonja az argumentum
grafikonja az argumentum ![]() valós értékeire.
valós értékeire.
![]()
Általánosabb függvényekkel való ábrázolás
A hiperbolikus érintőfüggvény ![]() általánosabb matematikai függvényekkel is ábrázolható. Mint a hiperbolikus szinusz- és koszinuszfüggvények hányadosa, amelyek az általánosított hipergeometriai, Bessel-, Struve- és Mathieu-függvények speciális esetei, a hiperbolikus érintőfüggvény is ábrázolható e speciális függvények hányadosaként. Ezek az ábrázolások azonban nem túl hasznosak. Hasznosabb, ha a hiperbolikus érintőfüggvényt egy speciális függvény sajátos eseteiként írjuk fel. Ezt megtehetjük kétszeresen periodikus Jacobi elliptikus függvények segítségével, amelyek a hiperbolikus érintőfüggvénybe degenerálódnak, ha második paraméterük
általánosabb matematikai függvényekkel is ábrázolható. Mint a hiperbolikus szinusz- és koszinuszfüggvények hányadosa, amelyek az általánosított hipergeometriai, Bessel-, Struve- és Mathieu-függvények speciális esetei, a hiperbolikus érintőfüggvény is ábrázolható e speciális függvények hányadosaként. Ezek az ábrázolások azonban nem túl hasznosak. Hasznosabb, ha a hiperbolikus érintőfüggvényt egy speciális függvény sajátos eseteiként írjuk fel. Ezt megtehetjük kétszeresen periodikus Jacobi elliptikus függvények segítségével, amelyek a hiperbolikus érintőfüggvénybe degenerálódnak, ha második paraméterük ![]() vagy
vagy ![]() :
:
![]()
![]()
A hiperbolikus érintőfüggvény definíciója komplex argumentumra
A komplex ![]() -síkon a
-síkon a ![]() függvényt ugyanazzal a képlettel határozzuk meg, mint amit valós értékekre használunk:
függvényt ugyanazzal a képlettel határozzuk meg, mint amit valós értékekre használunk:
![]()
![]()
Azokban a ![]() pontokban, ahol a
pontokban, ahol a ![]() -nek nullái vannak, az utóbbi képlet nevezője egyenlő nullával, és a
-nek nullái vannak, az utóbbi képlet nevezője egyenlő nullával, és a ![]() szingularitások (elsőrendű pólusok) vannak.
szingularitások (elsőrendű pólusok) vannak.
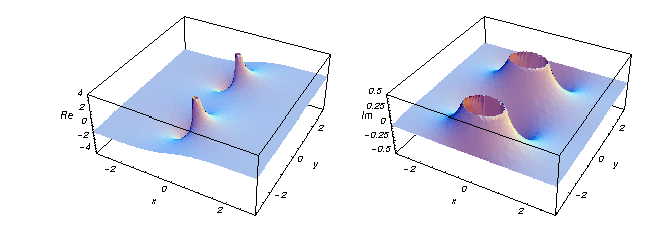
Itt van két grafikon, amely a hiperbolikus érintőfüggvény valós és képzetes részét mutatja a komplex sík felett.
![]()
A hiperbolikus érintőfüggvény legismertebb tulajdonságai és képletei
Értékek pontokban
A hiperbolikus érintő értékei argumentumának speciális értékeire könnyen levezethetők a kör érintőjének megfelelő értékeiből a kör speciális pontjaiban:
![]()
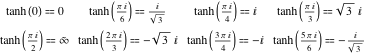
![]()
![]()
![]()
![]()
A végtelenben lévő értékek a következő képletekkel fejezhetők ki:
![]()
![]()
Általános jellemzők
A ![]() argumentum valós értékei esetén
argumentum valós értékei esetén ![]() értékei valósak.
értékei valósak.
A ![]() pontokban a
pontokban a ![]() értékei algebrai értékek. Több esetben lehetnek
értékei algebrai értékek. Több esetben lehetnek ![]() , 0 vagy ⅈ:
, 0 vagy ⅈ:
![]()
![]()
A ![]() értékeit csak négyzetgyökkel lehet kifejezni, ha
értékeit csak négyzetgyökkel lehet kifejezni, ha ![]() és
és ![]() egy 2-es hatvány és különböző Fermat-prímek {3, 5, 17, 257, …} szorzata.
egy 2-es hatvány és különböző Fermat-prímek {3, 5, 17, 257, …} szorzata.
A ![]() függvény a
függvény a ![]() analitikus függvénye, amely a teljes komplex
analitikus függvénye, amely a teljes komplex ![]() -síkon definiált, és nincsenek ágvágásai és ágpontjai. Végtelen sok szinguláris pontja van:
-síkon definiált, és nincsenek ágvágásai és ágpontjai. Végtelen sok szinguláris pontja van:
(a) ![]() az egyszerű pólusok 1 maradékkal.(b)
az egyszerű pólusok 1 maradékkal.(b) ![]() egy lényeges szinguláris pont.
egy lényeges szinguláris pont.
Ez egy ![]() periódusú periodikus függvény:
periódusú periodikus függvény:
![]()
![]()
![]()
![]()
A ![]() függvény egy tükörszimmetrikus páratlan függvény:
függvény egy tükörszimmetrikus páratlan függvény:
![]()
![]()
Differenciálás
A ![]() első deriváltjának egyszerű ábrázolásai vannak a
első deriváltjának egyszerű ábrázolásai vannak a ![]() függvény vagy a
függvény vagy a ![]() függvény segítségével:
függvény segítségével:
![]()
![]()
A ![]()
![]()
![]() deriváltjának sokkal bonyolultabb ábrázolásai vannak, mint a
deriváltjának sokkal bonyolultabb ábrázolásai vannak, mint a ![]() és
és ![]() szimbolikus
szimbolikus ![]()
![]() deriváltjainak:
deriváltjainak:
![]()
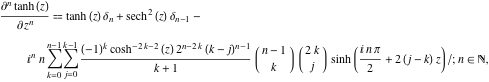
ahol ![]() a Kronecker-delta szimbóluma:
a Kronecker-delta szimbóluma: ![]() és
és ![]() .
.
Rendes differenciálegyenlet
A függvény ![]() a következő elsőrendű nemlineáris differenciálegyenletet teljesíti:
a következő elsőrendű nemlineáris differenciálegyenletet teljesíti:
![]()
![]()
Sorozatábrázolás
A ![]() függvénynek van egy egyszerű sorbővülése az origóban, amely minden véges
függvénynek van egy egyszerű sorbővülése az origóban, amely minden véges ![]() értékre konvergál
értékre konvergál ![]() -vel:
-vel:
![]()
![]()
mivel ![]() a Bernoulli-számok.
a Bernoulli-számok.
Integrál ábrázolás
A ![]() függvénynek van egy jól ismert integrál ábrázolása a következő határozott integrálon keresztül a valós tengely pozitív része mentén:
függvénynek van egy jól ismert integrál ábrázolása a következő határozott integrálon keresztül a valós tengely pozitív része mentén:
![]()
![]()
Folytonos tört ábrázolások
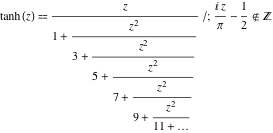
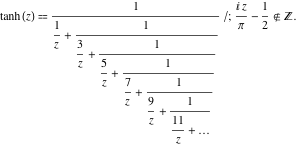
A ![]() függvénynek a következő egyszerű folytonos tört ábrázolásai vannak:
függvénynek a következő egyszerű folytonos tört ábrázolásai vannak:
![]()
![]()
Határozatlan integrálás
A hiperbolikus érintőfüggvényt tartalmazó kifejezések határozatlan integráljai néha elemi függvények segítségével fejezhetők ki. Az eredmények kifejezéséhez azonban gyakran speciális függvényekre van szükség, még akkor is, ha az integrálok egyszerű alakúak (ha zárt alakban kiértékelhetők). Íme néhány példa:
![]()
![]()
![]()
![]()
![]()
![]()
Határozott integrálás
A hiperbolikus érintőfüggvényt tartalmazó határozott integrálok néha egyszerűek. Például a híres Katalán-állandó ![]() a következő integrálon keresztül határozható meg:
a következő integrálon keresztül határozható meg:
![]()
![]()
Egyes speciális függvények segítségével bonyolultabb határozott integrálok is kiértékelhetők. Például a hipergeometriai függvényre van szükség a következő integrál kifejezéséhez:
![]()
![]()
Véges összegzés
A következő véges összeg, amely tartalmazza a hiperbolikus érintőfüggvényt, kifejezhető a hiperbolikus kotangens függvények segítségével:
![]()
![]()
Összeadási formulák
Az összeg hiperbolikus érintője a következő szabállyal ábrázolható: “az összeg hiperbolikus érintője egyenlő a hiperbolikus érintő összegének eggyel osztott összege és a hiperbolikus érintő szorzata”. Hasonló szabály érvényes a különbség hiperbolikus érintőjére is:
![]()
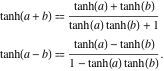
Több argumentum
Több argumentum ![]() ,
, ![]() , … esetén a
, … esetén a ![]() függvény a véges összegek hányadosaként ábrázolható, amely a hiperbolikus érintő hatványait tartalmazza:
függvény a véges összegek hányadosaként ábrázolható, amely a hiperbolikus érintő hatványait tartalmazza:
![]()
![]()
![]()
![]()
![]()
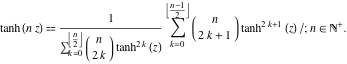
Félszög képletek
A félszög hiperbolikus érintője két hiperbolikus függvény segítségével a következő egyszerű képletekkel ábrázolható:
![]()
![]()
![]()
![]()
A hiperbolikus szinuszfüggvény az utolsó képletben a hiperbolikus koszinuszfüggvénnyel helyettesíthető. Ez azonban egy bonyolultabb, vízszintes sávban érvényes ábrázoláshoz vezet:
![]()
![]()
A képlet kismértékű módosításával az utolsó megszorítás megszüntethető (most már az azonosság minden komplex ![]() -ra érvényes):
-ra érvényes):
![]()
![]()
Két egyenes függvény összege
Két hiperbolikus érintőfüggvény összege a következő szabállyal írható le: “a hiperbolikus érintőfüggvények összege egyenlő az összeg hiperbolikus szinuszának és a hiperbolikus szekánsok szorzatával”. Hasonló szabály érvényes két hiperbolikus érintő különbségére is:
![]()
![]()
Az egyenes függvényt tartalmazó termékek
A két hiperbolikus érintőfüggvény szorzata, valamint a hiperbolikus érintő és a kotangens szorzata a következő ábrázolásokkal rendelkezik:
![]()
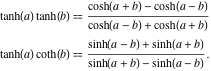
Egyenlőtlenségek
A hiperbolikus érintőfüggvényre vonatkozó leghíresebb egyenlőtlenség a következő:
![]()
![]()
Kapcsolatok a fordított függvényével
A ![]() függvény és a
függvény és a ![]() fordított függvénye között egyszerű összefüggések vannak:
fordított függvénye között egyszerű összefüggések vannak:
![]()
![]()
![]()
![]()
A második képlet legalább a ![]() vízszintes sávban érvényes. Ezen a sávon kívül egy sokkal bonyolultabb összefüggés (amely tartalmazza az egységlépést, a valós részt és a padlófüggvényeket) érvényes:
vízszintes sávban érvényes. Ezen a sávon kívül egy sokkal bonyolultabb összefüggés (amely tartalmazza az egységlépést, a valós részt és a padlófüggvényeket) érvényes:
![]()
![]()
Más hiperbolikus függvényeken keresztül történő ábrázolások
A hiperbolikus érintő- és kotangensfüggvényeket egy nagyon egyszerű képlet köti össze, amely tartalmazza a lineáris függvényt az argumentumban:
![]()
![]()
A hiperbolikus érintőfüggvény más hiperbolikus függvényeken keresztül is ábrázolható a következő képletekkel:
![]()
![]()
![]()
![]()
Ábrázolások trigonometrikus függvényeken keresztül
A hiperbolikus érintőfüggvénynek vannak olyan ábrázolásai, amelyek trigonometrikus függvényeket használnak:
![]()
![]()
![]()
![]()
Alkalmazások
A hiperbolikus érintőfüggvényt az egész matematikában, az egzakt tudományokban és a mérnöki tudományokban használják.