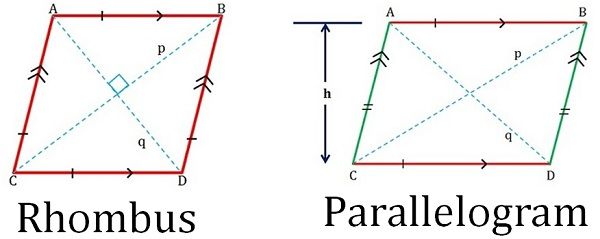
I geometrien er der mange typer af firkanter, dvs. parallelogram, rhombe, kvadrat, rektangel, trapez og drage, som har fælles karakteristika, hvilket gør det svært for folk at forstå disse figurer. En rhombe kan betegnes som et skråt kvadrat, hvis tilstødende sider er lige store. Et parallelogram er derimod et skråt rektangel med to sæt parallelle modsatte sider.
Den grundlæggende forskel mellem rhombe og parallelogram ligger i deres egenskaber, dvs. at alle siderne i en rhombe har samme længde, mens parallelogrammet er en retvinklet figur, hvis modsatte sider er parallelle.
Indhold: Rhombe vs. parallelogram
- Sammenligningsskema
- Definition
- Nøgleforskelle
- Konklusion
Sammenligningsskema
| Basis for sammenligning | Rombus | Parallelogram |
|---|---|---|
| Betydning | Rombus henviser til et fladformet, firsidet figur med alle sider kongruente. | Et parallelogram er en firsidet fladformet figur, hvis modsatte sider er parallelle med hinanden. |
| Lige sider | Alle fire sider har samme længde. | Modstående sider har samme længde. |
| Diagonaler | Diagonalerne skærer hinanden i rette vinkler og danner en scalene trekant. | Diagonalerne skærer hinanden i halve vinkler og danner to kongruente trekanter. |
| Areal | (pq)/2, hvor p og q er diagonalerne | bh, hvor b = grundflade og h = højde |
| Omkreds | 4 a, hvor a = side | 2 (a+b), hvor a = side, b = base |
Definition af rhombe
En firsidig, hvis sidelængder er kongruente, kaldes en rhombe. Den er fladformet og har fire sider, hvor de modstående sider er parallelle med hinanden (se figuren nedenfor).
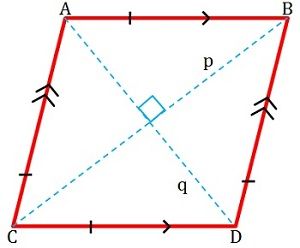De modsatte vinkler i en rhombe er lige store, dvs. af samme grad. Dens diagonaler møder hinanden i 90 grader (ret vinkel), og er derfor vinkelrette på hinanden og danner to ligesidede trekanter. Dens tilstødende sider er komplementære, hvilket betyder, at summen af deres mål er lig med 180 grader. Det er også kendt som et ligesidet parallelogram.
Definition af parallelogram
Et parallelogram er som navnet antyder et beskrives som en flad formet figur, der har fire sider, hvis sæt af modsatte sider er parallelle og kongruente (se nedenstående figur).
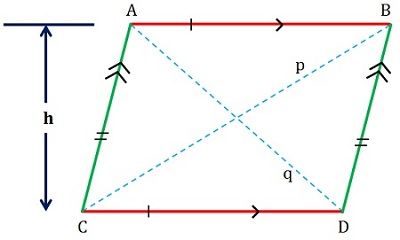Målet på de modstående vinkler er lige store, og de på hinanden følgende vinkler er komplementære, dvs. at summen af deres mål er lig med 180 grader. Dens diagonaler halverer hinanden, der danner to kongruente trekanter.
Nøgleforskelle mellem rhombus og parallelogram
Skellen mellem rhombus og parallelogram kan tegnes tydeligt på følgende grundlag:
- Vi definerer rhombus som en fladformet, firsidet firkant, hvis længde på alle sider er kongruent. Et parallelogram er en firsidet fladformet figur, hvis modsatte sider er parallelle med hinanden.
- Alle siderne i en rhombe er lige lange, mens kun de modsatte sider i et parallelogram er lige lange.
- Diagonalerne i en rhombe halverer hinanden i rette vinkler og danner to scalene trekanter. I modsætning til et parallelogram, hvis diagonaler skærer hinanden i to dele og danner to kongruente trekanter.
- Den matematiske formel for rhombusens areal er (pq)/2, hvor p og q er diagonalerne. Omvendt kan arealet af parallelogrammet beregnes ved at gange basis og højde.
- Rombens omkreds kan beregnes ved hjælp af følgende formel – 4 a, hvor a = siden af rhomben. Omkredsen af parallelogrammet kan derimod beregnes ved – at lægge base og højde sammen og gange summen med 2.
Slutning
Både parallelogrammet og rhomben er kvadrilaterale, hvis modstående sider er parallelle, modsatte vinkler er lige store, summen af de indvendige vinkler er 360 grader. En rhombe er i sig selv en særlig form for parallelogram. Derfor kan man sige, at enhver rhombe er et parallelogram, men det omvendte er ikke muligt.