Tom-Cook-algoritmen
Her lærer vi en genial anvendelse af en divide and conquer-algoritme kombineret med lineær algebra til at multiplicere store tal, hurtigt. Og en introduktion til big-O notation!
Dette resultat er faktisk så kontra-intuitivt, at den store matematiker Kolmogorov formodede, at en så hurtig algoritme ikke fandtes.
Del 0: Lang multiplikation er langsom multiplikation. (Og en introduktion til Big-O Notation)
Vi kan alle huske, at vi lærte at multiplicere i skolen. Faktisk har jeg en tilståelse at gøre. Husk, at dette er en zone uden domme 😉
I skolen havde vi “våd leg”, når det regnede for meget til at lege på legepladsen. Mens de andre (normale/glade/glade-elskende/positive-adjektiv-af-valg) børn legede spil og fjollede rundt, tog jeg nogle gange et stykke papir og multiplicerede store tal sammen, bare for hyggens skyld. Den rene glæde ved at regne! Vi havde endda en multiplikationskonkurrence, “Super 144”, hvor vi skulle multiplicere et 12 gange 12 gitter af tal (fra 1 til 12) så hurtigt som muligt. Jeg øvede mig religiøst på dette, i en sådan grad at jeg havde mine egne forberedte øvelsesark, som jeg fotokopierede og derefter brugte på skift. Til sidst fik jeg min tid ned på 2 minutter og 1 sekund, hvor min fysiske grænse for at kradse var nået.
Trods denne besættelse af multiplikation faldt det mig aldrig ind, at vi kunne gøre det bedre. Jeg brugte så mange timer på at gange, men jeg forsøgte aldrig at forbedre algoritmen.
Tænk på at gange 103 med 222.
Vi beregner 2 gange 3 gange 1 + 2 gange 0 gange 10 + 2 gange 1 gange 100 + 20 gange 3 gange 1 + 20 gange 0 gange 10 + 20 gange 1 gange 100 = 22800
Generelt set kræver det O(n²) operationer at gange til n cifre for at gange med n tal. Den “store O”-notation betyder, at hvis vi skulle tegne en graf over antallet af operationer som en funktion af n, er det i virkeligheden n²-udtrykket, der betyder noget. Formen er i det væsentlige kvadratisk.
I dag vil vi opfylde alle vores barndomsdrømme og forbedre denne algoritme. Men først! Big-O venter os.
Big-O
Se på de to grafer nedenfor

Spørg en matematiker: “Er x² og x²+x^(1/3) det samme?”, og de vil sandsynligvis kaste op i deres kaffekop og begynde at græde, og mumle noget om topologi. Det var i hvert fald min reaktion (i begyndelsen), og jeg ved næppe noget om topologi.
Okay. De er ikke det samme. Men vores computer er ligeglad med topologi. Computere adskiller sig i ydeevne på så mange måder, som jeg ikke engang kan beskrive, fordi jeg intet ved om computere.
Men det nytter ikke noget at finjustere en damptromle. Hvis to funktioner for store værdier af deres input vokser i samme størrelsesorden, så indeholder det til praktiske formål det meste af den relevante information.
I grafen ovenfor ser vi, at de to funktioner ser ret ens ud for store input. Men på samme måde ligner x² og 2x² hinanden – sidstnævnte er kun dobbelt så stor som den første. Ved x = 100 er den ene 10.000 og den anden 20.000. Det betyder, at hvis vi kan beregne den ene, kan vi sandsynligvis også beregne den anden. Hvorimod en funktion, der vokser eksponentielt, lad os sige 10^x, ved x = 100 allerede er langt langt større end antallet af atomer i universet. (10¹⁰⁰ >>>>> 10⁸⁰ som er et estimat, Eddington-tallet, på antallet af atomer i universet ifølge min Googling*).
* faktisk brugte jeg DuckDuckGo.
At skrive hele tal som polynomier er både meget naturligt og meget unaturligt. At skrive 1342 = 1000 + 300 + 40 + 2 er meget naturligt. At skrive 1342 = x³+3x²+4x + 2, hvor x = 10, er lidt mærkeligt.
Generelt set kan man antage, at man ønsker at gange to store tal, skrevet i base b, med n cifre hver. Vi skriver hvert n-cifret tal som et polynomium. Hvis vi deler det n-cifrede tal op i r stykker, har dette polynomium n/r termer.
Lad f.eks. b = 10, r = 3, og vores tal er 142 122 912
Vi kan lave dette om til
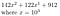
Dette fungerer meget fint, når r = 3, og vores tal, skrevet i base 10, havde 9 cifre. Hvis r ikke deler n perfekt, så kan vi bare tilføje nogle nuller foran. Igen illustreres dette bedst med et eksempel:
27134 = 27134 + 0*10⁵ = 027134, som vi repræsenterer som
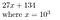
Hvorfor kan dette være nyttigt? For at finde koefficienterne til polynomiet P, hvis polynomiet er af orden N, kan vi bestemme koefficienterne ved at udtage det i N+1 punkter ved at prøveudtage det i N+1 punkter.
Til eksempel: Hvis polynomiet x⁵ + 3x³ +4x-2, som er af orden 5, samples i 6 punkter, kan vi derefter udregne hele polynomiet.
Intuitivt har et polynomium af orden 5 6 koefficienter: koefficienten for 1, x, x², x³, x⁴, x⁵. Givet 6 værdier og 6 ubekendte kan vi finde ud af værdierne.
(Hvis du kan lineær algebra, kan du behandle de forskellige potenser af x som lineært uafhængige vektorer, lave en matrix til at repræsentere informationen, invertere matrixen, og voila)
Sampling af polynomier for at bestemme koefficienter (valgfrit)
Her ser vi lidt mere indgående på logikken bag sampling af et polynomium for at udlede dets koefficienter. Du er velkommen til at springe til næste afsnit.
Det, vi vil vise, er, at hvis to polynomier af grad N stemmer overens på N+1 punkter, så må de være ens. Dvs. at N+1 punkter entydigt angiver et polynomium af orden N.
Tænk på et polynomium af orden 2. Dette er af formen P(z) = az² +bz + c. I henhold til algebraens fundamentale sætning – skamløs, plug her, jeg har brugt flere måneder på at samle et bevis for dette, og derefter skrive det op, her – kan dette polynomium faktoriseres. Det betyder, at vi kan skrive det som A(z-r)(z-w)
Bemærk, at polynomiet ved z = r og ved z = w evalueres til 0. Vi siger, at w og r er rødder af polynomiet.
Nu viser vi, at P(z) ikke kan have mere end to rødder. Lad os antage, at det har tre rødder, som vi kalder w, r, s. Vi faktoriserer derefter polynomiet. P(z) = A(z-r)(z-w). Så er P(s) = A(s-r)(s-w). Dette er ikke lig med 0, da multiplikation af tal, der ikke er nul, giver et tal, der ikke er nul. Dette er en modsigelse, fordi vores oprindelige antagelse var, at s var en rod i polynomiet P.
Dette argument kan anvendes på et polynomium af orden N på en stort set identisk måde.
Så lad os nu antage, at to polynomier P og Q af orden N stemmer overens på N+1 punkter. Så er P-Q, hvis de er forskellige, et polynomium af orden N, som er 0 i N+1 punkter. I henhold til det foregående er dette umuligt, da et polynomium af orden N højst har N rødder. Vores antagelse må således have været forkert, og hvis P og Q stemmer overens i N+1 punkter, er de det samme polynomium.
Seeing is believing: Et arbejdseksempel
Lad os se på et virkelig stort tal, som vi kalder p. I base 10 er p 24 cifre langt (n=24), og vi vil dele det i 4 stykker (r=4). n/r = 24/4 = 6
p = 292.103.243.859.143.157.364.152.
Og lad det polynomium, der repræsenterer det, hedde P,
P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152
med P(10⁶) = p.
Da graden af dette polynomium er 3, kan vi udregne alle koefficienterne ved at tage stikprøver på 4 steder. Lad os få en fornemmelse af, hvad der sker, når vi prøver det på nogle få punkter.
- P(0) = 364.152
- P(1) = 1.043.271
- P(-1) = 172.751
- P(2) = 3.962.726
Det er påfaldende, at disse alle har 6 eller 7 cifre. Det er sammenlignet med de 24 cifre, der oprindeligt findes i p.
Lad os gange p med q. Lad q = 124.153.913.241.241.143.634.899.130, og
Q(x) = 124.153 x³ + 913.241 x²+143.634 x + 899.130
Det kunne være forfærdeligt at beregne t=pq. Men i stedet for at gøre det direkte, prøver vi at beregne polynomiumrepræsentationen af t, som vi betegner T. Da P er et polynomium af orden r-1=3, og Q er et polynomium af orden r-1 = 3, er T et polynomium af orden 2r-2 = 6.
T(10⁶) = t = pq
T(10⁶) = P(10⁶)Q(10⁶)
Tricket er, at vi vil regne koefficienterne i T ud, i stedet for direkte at gange p og q sammen. Så er det nemt at udregne T(1⁰⁶), fordi vi for at gange med 1⁰⁶⁶ bare sætter 6 nuller på bagsiden. Det er også let at summere alle delene, fordi addition er en meget billig handling for computere at udføre.
For at beregne T’s koefficienter skal vi prøve det i 2r-1 = 7 punkter, fordi det er et polynomium af orden 6. Vi ønsker sandsynligvis at vælge små hele tal, så vi vælger
- T(0)=P(0)Q(0)= 364.152*899.130
- T(1)=P(1)Q(1)= 1.043.271*2.080.158
- T(2)=P(2)Q(2)= 3.962.726*5.832,586
- T(-1)=P(-1)Q(-1)= 172751*1544584
- T(-2)=P(-2)Q(-2)= -1.283.550*3.271,602
- T(3)=P(-3)Q(-3)= -5,757,369*5,335,266
Opmærksomheden henledes på størrelsen af P(-3), Q(-3), P(2), Q(2) osv… Det er alle tal med ca. n/r = 24/4 = 6 cifre. Nogle er 6 cifre, andre er 7. Efterhånden som n bliver større, bliver denne tilnærmelse mere og mere rimelig.
Så vidt vi har reduceret problemet til følgende trin, eller algoritme:
(1) Beregn først P(0), Q(0), P(1), Q(1) osv. (lavomkostningshandling)
(2) For at få vores 2r-1= 7 værdier af T(x) skal vi nu gange 2r-1 tal af tilnærmelsesvis størrelse n/r cifre lange. Vi skal nemlig beregne P(0)Q(0), P(1)Q(1), P(-1)Q(-1), osv. (Handling med høje omkostninger)
(3) Rekonstruer T(x) ud fra vores datapunkter. (Lavomkostningshandling: men vil komme i betragtning senere).
(4) Med vores rekonstruerede T(x) evalueres T(10⁶) i dette tilfælde
Dette fører pænt til en analyse af køretiden for denne fremgangsmåde.
Løbetid
Fra ovenstående fandt vi ud af, at omkostningerne ved at gange to n-cifrede tal med Tooms algoritme vil adlyde:
Det er det, vi så i det udførte eksempel. At gange hver P(0)Q(0), P(1)Q(1) osv. koster T(n/r), fordi vi gangsætter to tal af længde ca. n/r. Vi skal gøre dette 2r-1 gange, da vi ønsker at prøve T(x) – som er et polynomium af orden 2r-2 – på 2r-1 steder.
Hvor hurtigt er dette? Vi kan løse denne slags ligning eksplicit.

Det eneste, der nu mangler, er nogle rodet algebra
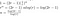
Som der var nogle andre omkostninger fra matrixmultiplikationsprocessen (‘reassembling’), og fra additionen, kan vi ikke rigtig sige, at vores løsning er den nøjagtige løbetid, så i stedet konkluderer vi, at vi har fundet den store-O af løbetiden
Optimering af r
Denne løbetid afhænger stadig af r. Retter r, og så er vi færdige. Men vores nysgerrighed er endnu ikke tilfredsstillet!
Da n bliver stor, ønsker vi at finde en tilnærmelsesvis optimal værdi for vores valg af r. Dvs. vi ønsker at vælge en værdi af r, som ændrer sig for forskellige værdier af n.
Det vigtigste her er, at når r varierer, skal vi være lidt opmærksomme på omkostningerne ved reassemblering – den matrix, der udfører denne operation, har en omkostning på O(r²). Da r var fast, behøvede vi ikke at se på det, for da n voksede sig stor med r fast, var det de termer, der involverede n, der bestemte væksten i hvor meget beregning der var nødvendig. Da vores optimale valg af r vil blive større, når n bliver større, kan vi ikke længere ignorere dette.
Denne sondring er afgørende. I første omgang valgte vi i vores analyse en værdi af r, måske 3, måske 3 milliarder, og så kiggede vi på big-O-størrelsen, efterhånden som n voksede vilkårligt stort. Nu ser vi på adfærden, når n vokser vilkårligt stort, og r vokser med n med en eller anden hastighed, som vi bestemmer. Denne ændring af perspektivet ser på O(r²) som en variabel, mens da r blev holdt fast, var O(r²) en konstant, om end en vi ikke kendte.
Så vi opdaterer vores analyse fra før:
hvor O(r²) repræsenterer omkostningerne ved reassembleringsmatrixen. Vi ønsker nu at vælge en værdi af r for hver værdi af n, som tilnærmelsesvis minimerer dette udtryk. For at minimere prøver vi først at differentiere med hensyn til r. Dette giver det noget hæsligt udseende udtryk

Normalt set, for at finde minimumspunktet, sætter vi den afledte lig med 0. Men dette udtryk har ikke et pænt minimum. I stedet finder vi en “god nok” løsning. Vi bruger r = r^(sqrt(logN))) som vores guestimate-værdi. Grafisk set er dette ret tæt på minimum. (I diagrammet nedenfor er 1/1000-faktoren der for at gøre grafen synlig i rimelig skala)
Den nedenstående graf viser vores funktion for T(N), skaleret med en konstant, med rødt. Den grønne linje er ved x = 2^sqrt(logN), som var vores guestimate-værdi. ‘x’ træder i stedet for ‘r’, og i hvert af de tre billeder er der anvendt en anden værdi for N.



Dette er ret overbevisende for mig om, at vores valg var et godt valg. Med dette valg af r kan vi sætte det ind og se, hvordan vores algoritmes endelige big-O:

hvor vi blot satte vores værdi for r ind og brugte en tilnærmelse for log(2r-1)/log(r), som er meget nøjagtig for store værdier af r.
Hvor stor en forbedring?
Måske var det rimeligt, at jeg ikke opdagede denne algoritme, da jeg var en lille dreng, der lavede multiplikation. I nedenstående graf giver jeg koefficienten for vores big-O-funktion til 10 (til demonstrationsformål) og dividerer den med x² (da den oprindelige fremgangsmåde til multiplikation var O(n²)). Hvis den røde linje tenderer mod 0, ville det vise, at vores nye løbetid asymptotisk set gør det bedre end O(n²).
Og faktisk, selv om formen på funktionen viser, at vores fremgangsmåde i sidste ende er hurtigere, og i sidste ende er den meget hurtigere, skal vi vente, til vi har næsten 400 cifre lange tal, før dette er tilfældet! Selv hvis koefficienten kun var 5, skulle tallene være omkring 50 cifre lange for at se en hastighedsforbedring.

For mit 10-årige jeg ville det være lidt af en udfordring at gange 400 cifre med tal! At holde styr på de forskellige rekursive kald af min funktion ville også være noget skræmmende. Men for en computer, der udfører en opgave inden for AI eller fysik, er dette et almindeligt problem!
Hvor dybtgående er dette resultat?
Hvad jeg elsker ved denne teknik er, at den ikke er raketvidenskab. Det er ikke den mest forbløffende matematik, der nogensinde er blevet opdaget. Set i bakspejlet virker det måske indlysende!
Men det er netop det, der er matematikkens genialitet og skønhed. Jeg har læst, at Kolmogorov på et seminar formodede, at multiplikation grundlæggende set var O(n²). Kolmogorov opfandt i grunden masser af moderne sandsynlighedsteori og analyse. Han var en af det 20. århundredes store matematiske personligheder. Alligevel viste det sig, at der i forbindelse med dette uvedkommende område var et helt korpus af viden, der ventede på at blive opdaget, og som sad lige under hans og alle andres næser!
Der er faktisk algoritmer af typen Divide and Conquer, som man ret hurtigt kommer til at tænke på i dag, fordi de er så almindeligt anvendte. Men de er et produkt af computerrevolutionen, idet det først er med den enorme beregningskraft, at menneskelige hjerner har fokuseret specifikt på beregningshastighed som et område af matematikken, der er værd at studere i sin egen ret.
Det er derfor, at matematikere ikke bare er villige til at acceptere, at Riemann-hypotesen er sand, bare fordi det ser ud til, at den kunne være sand, eller at P ikke er lig med NP, bare fordi det virker mest sandsynligt. Matematikkens vidunderlige verden bevarer altid en evne til at forvirre vores forventninger.
Faktisk set kan man finde endnu hurtigere måder at gange på. De bedste metoder i øjeblikket anvender hurtige fouriertransformationer. Men det gemmer jeg til en anden dag 🙂
Lad mig vide, hvad du mener nedenunder. Jeg er nyligt på Twitter som ethan_the_mathmo, du kan følge mig her.
Jeg stødte på dette problem i en vidunderlig bog jeg bruger kaldet ‘The Nature of Computation’ af fysikerne Moore og Mertens, hvor et af problemerne guider dig gennem en analyse af Tooms algoritme.