Sådan hjælper du elever, der kæmper med ordproblemer

“De kender matematikken. De kan bare ikke løse ordproblemerne. Det er deres læseforståelse.”

Mrs. Hartwell forklarede, hvorfor hendes elever havde haft det svært ved de statslige prøver. Hun kendte sine elever og havde foretaget en omfattende vurdering. Hun var sikker på, at deres vanskeligheder var et problem med læse- og skrivefærdigheder.

“Jeg forstår ikke, hvorfor de gør det så svært at læse. Børnene tager allerede en prøve i sprogkunst.”

Jeg var blevet matchet med fru Hartwell (og andre på hendes skole) som en del af et program i New York City, der skulle øge resultaterne i matematik. Målet var at bringe konceptuel matematik ind på “Tier 1”-skoler. Tier 1-skoler var de skoler, der var førende i byen på tre områder. Laveste indkomst, laveste testresultater og højeste procentdel af farvede elever.

Jeg havde hørt forklaringen om “læse- og skrivefærdigheder” fra andre lærere i programmet. Og det gav faktisk mening. Hvis eleverne kunne matematik, hvorfor havde de så ellers problemer med testen, som indeholdt mange ordproblemer?

Men der var en hage ved det. I løbet af de sidste tre år var læse- og skrivefærdighederne steget fra 30-40 % i hele byen. I samme periode var resultaterne i matematik stort set uændret.

Hvis det var et problem med læsning, burde stigninger i læsepræstationer udløse en eksplosiv vækst i matematik. Desuden virkede sproget i ordopgaverne bare ikke kompliceret nok til at skabe problemer.

Den næste time skulle jeg besøge Ms. Hartwells klasse. Hun havde planlagt en lektion om ordproblemer, så jeg kunne se problemet med egne øjne.

Over-Scaffolding Word Problems

De studerende sad ved runde borde, og hun stod forrest. Hun og hendes elever havde alle håndholdte whiteboards.

De slog deres lærebøger op på side 47, og hun læste et ordproblem højt. “Sarah har 40 pund gulerødder til sine heste. Hvis hun har 100 heste, hvor mange pund får hver hest så?”

“OK klassen, hun har 40 pund, som hun vil give til hver hest. Så hvilken operation skal vi bruge?”

Hun pegede på en ankertavle, hvor der stod “nøgleord” for hver operation. ‘Hver’ stod øverst på listen over opdeling.

“Opdeling!” svarede klassen.

“Rigtigt. Så hvordan dividerer vi et lille tal med et stort tal?”

Klassen var stille. Ms. Hartwell tegnede et vinculum (hus til lang division) på sin whiteboardtavle. Eleverne kopierede, mens hun satte 40 under huset og 100 udenfor.

“Nu passer 100 ikke ind i 40, så vi er nødt til at tilføje et decimal.” Hun ændrede 40 til 40,0. “Hvor mange gange går 100 ind i 400?”

Et par elever råbte: “Fire!”

“Præcis. Nu skal vi også sætte et decimaltal i vores kvotienten. Vores endelige svar er?”

Klassen læste svaret, “0,4”, fra hendes whiteboard.

Hun gav en lignende opgave og pegede på “CUBES”-plakaten på væggen. “Husk at sætte en cirkel om tallene og sætte en boks om nøgleordene.”

Hun cirkulerede rundt, mens eleverne arbejdede. Nogle spurgte, hvor de skulle sætte decimalerne. Andre havde problemer med at sætte subtraktionsdelen af den lange division på linje. Nogle elever arbejdede parvis, hvor den ene lavede udregningen, mens den anden kopierede.

I slutningen af lektionen havde alle det rigtige svar på deres papir. “Kan du se?”

Hvad gik galt?

Selv om dette er et ekstremt eksempel, er mange af de fejl, som fru Hartwell begik, faktisk ret almindelige.

Over-scaffolding opstår, når vi giver eleverne for meget støtte. Mens det er almindeligt, at pædagoger sætter en ære i at give eleverne “så meget støtte, som de har brug for”, er overscaffolding noget andet.

Begrebet “scaffolding” stammer fra Lev Vygotskys arbejde. Han opfandt begrebet “Zone for proximal udvikling”. ZPD omfatter ting, der er lige uden for en lærendes rækkevidde. De kan ikke helt klare det på egen hånd, men de kan klare det med støtte. Ved hjælp af “stilladsering” kan vi flytte disse færdigheder ind i en lærendes centrale færdigheder.

Det, der ofte overses, er, at stilladsering kun gælder for færdigheder, der allerede befinder sig i en lærendes ZPD. Der er en lang række færdigheder, som i øjeblikket er uden for en lærendes rækkevidde. Når vi forsøger at stille disse færdigheder til rådighed, gør vi mere skade end gavn.

Et af problemerne med overdreven stilladsering er, at eleverne aldrig internaliserer de målrettede færdigheder. Når vi hjælper en elev med noget, der ligger uden for deres ZPD, vil de altid have brug for vores hjælp. I hvert fald indtil vi identificerer de mellemliggende færdigheder, der ligger inden for deres ZPD.

Et andet problem er, at over-scaffolding giver os en falsk følelse af succes. I dette tilfælde troede fru Hartwell, at hendes elever kunne “klare matematikken” i ordproblemet. I virkeligheden efterlignede de blot hendes handlinger. Der var ingen grund til at tro, at de kunne finde en lignende løsning på egen hånd.

Hun fjernede også hele processen med “formulering” fra problemløsningsprocessen. Mange undervisere tænker på forståelse og formulering som det samme, men formulering er en separat matematisk kompetence.

Og det kan netop være den manglende ingrediens i den måde, du i øjeblikket underviser i ordproblemer.

Classroom Resources and Professional Learning

Formulering: Nøglen til succes med ordproblemer

Formulering af ordproblemer indebærer, at man skal forstå dem. Men det går videre end det. Formulering minder mere om oversættelse end om forståelse.

Når en elev læser et ordproblem, skal han eller hun først omdanne bogstaver til lyde (afkodning). Derefter skal de forstå, hvad ordene betyder (ordforråd). De skal forstå, hvordan ordene passer sammen i en sætning (syntaks). Endelig kommer forståelsen ved at sætte disse dele sammen til en mening.

De fleste elever i 6. klasse kunne læse fru Hartwells opgave og nemt forstå, at Sarah uddeler gulerødder til sine heste. Men langt færre vil forbinde “delingen” af gulerødder med division.

Dette er den del, der får mange undervisere til at snuble. Det virker så indlysende for os. “Hun deler bogstaveligt talt gulerødderne op. Hvordan kan de ikke se, at det er deling.”

Det gør de bare ikke. Hvis de gjorde det, ville du ikke se nøgleordsskemaer hænge i matematiklokalerne. Og det hele går tilbage til dengang vi først underviste i operationer.

Hvorfor eleverne kæmper med formuleringen

Mange lærere på mange skoler lærer eleverne, at matematik er et fag, der handler om at skabe mening. Men i andre lærer man matematik som et fag, der handler om at huske.

Et eksempel på ‘matematik som huskeri’ er, når eleverne lærer matematiske fakta udenad. Men algoritmer handler også om at huske. Læg 120 oven på 47. Følg disse trin for at addere, disse for at subtrahere subtrahere, og disse for at multiplicere.

De studerende kan gentage disse trin uden at forstå størrelsen af tallene eller endda hvad operationerne betyder.

Når vi starter med begreber (ved at bruge visuelle modeller eller talsætninger), lærer de studerende, hvad operationerne betyder. Når vi går direkte til en algoritme, tænker eleverne på operationer som en række tilfældige trin.

År efter år får vi eleverne til at huske og gentage. De gennemfører den samme algoritme 30 gange som hjemmeopgave. Ændr tallene, og processen forbliver den samme. Men giv dem en ordopgave, og nu skal de finde mening.

Hvad prøverne fortæller os om ræsonnement

Vi kunne give vores elever 10 opgaver med titlen “Divisionsordproblemer”, for at gøre det lettere. De behøver ikke engang at læse problemerne. De skal blot regne ud (eller gætte), hvilket tal der er divisoren og hvilket tal der er dividende.

Men når eleverne sidder til en statsprøve, er målet ikke at gøre det lettere. Målet er at vurdere, hvad de kan gøre på egen hånd.

Prøvedeltagerne ønsker ikke at fortælle dem, hvilken operation de skal bruge. De vil endda sætte nøgleord for division og addition ind i den samme opgave. “Der er 20 elever i klassen. Hvis hvert barn har tre dollars, hvor meget har de så i alt?”

Så når eleverne kæmper med ordproblemer, handler det ikke kun om ordproblemerne. Det betyder som regel, at de laver matematik ud fra hukommelsen. Vi er nødt til at lære dem, at matematik handler om at skabe mening.

Studenterne har brug for strategier og processer for at løse ordproblemer

En del af problemet med et system som CUBES er, at det kalder sig selv en strategi, men i virkeligheden er det en proces.

En proces er en række trin. Når man først har identificeret en effektiv proces, kan man gentage den igen og igen uden at tænke for meget over. Algoritmer er en proces. Ligesom det er at stille sig på række “fra den højeste til den korteste” for at gå til frokost.

En strategi er noget andet. Strategier kræver en dyb forståelse. Og evnen til at anvende forståelsen i nye situationer.

Vi kan ikke forberede eleverne på alle de scenarier, de vil støde på i en ordopgave. Nogle kræver, at de kombinerer forskellige matematiske færdigheder, som de aldrig har kombineret før. Eller de kan kræve, at eleverne ændrer rækkefølgen af trinene for at finde frem til den korrekte løsning.

Tænk på følgende:

Du har 5 galloner juice til et skolearrangement med 100 elever. Hvis hver kop indeholder 3 oz, hvor mange kopper kan hver elev så drikke? Hvor meget vil der være tilbage.

En problemløsningsproces kan hjælpe eleverne med at begynde at løse dette problem. “Identificer, hvad der bliver spurgt om.” “Overvej, hvilke oplysninger der gives.”

Men der er ingen fast proces, vi kan lære dem at løse det rent faktisk. Det er her, strategien kommer ind i billedet. De er nødt til at omregne enheder. Erkende, at vi dividerer med rester, i stedet for at dividere fuldstændigt. De skal nok også omordne operationerne og dele saften i kopper, før de dividerer med antallet af elever.

Der er ikke noget “trick”, der får eleverne dertil. De er nødt til at forstå betydningen af operationerne. De har brug for at forstå matematik som et fag, hvor man skaber mening. Og de skal gentagne gange øve sig i at anvende strategisk tænkning på ordproblemer.

Polya-processen til løsning af ordproblemer

George Pólya var en indflydelsesrig ungarsk matematiker og Stanford-professor, der fandt en proces, der kunne bruges til at løse ethvert problem. Hans arbejde har berørt utallige matematikere og undervisere, hvoraf de fleste ikke kender hans navn.

Faktisk set er CUBES og andre såkaldte problemløsningsstrategier løseligt baseret på hans arbejde. Problemet er, at de forsøger at forenkle det. I den proces fjerner de alt, hvad der ligner dybdegående tænkning.

Polya mente, at ethvert problem kunne løses i fire trin: Forstå, planlægge, løse og reflektere. Jeg mener, at Polya’s oprindelige firetrins-proces er helt fin til brug i skoler.

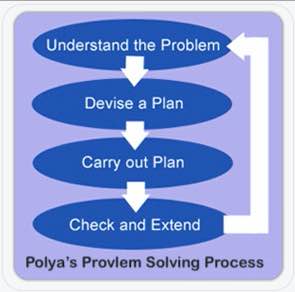For at forstå problemet identificerer vi, hvilke oplysninger der er givet, og hvad vi ønsker at finde. Det er her, hvor “C” og “U” i terninger kommer fra. Hvis eleverne ønsker at sætte en cirkel om tallene og understrege spørgsmålet, er det fint. Jeg foretrækker, at de skriver dem (med enheder) i et grafisk skema, i det mindste i begyndelsen. Det hjælper dem med at bearbejde det, de læser. Det hjælper også mig som lærer til at vurdere deres forståelse, mens jeg går rundt i lokalet.

Næste del er den vanskelige del. Det er i “planen”, at vi formulerer problemet. Vi tager et scenarie fra den virkelige verden og omdanner det til en anden matematisk repræsentation.

Det tredje trin er at løse. Hvis vi har formuleret korrekt, er det her, vi beregner. Eleverne bruger normalt en algoritme, men jeg opfordrer også til at bruge ligninger og visuelle modeller.

Sidst ser eleverne tilbage og kontrollerer deres arbejde. De bør også reflektere over deres proces. Hvis jeg har begået en fejl, hvorfor så? Kunne denne strategi hjælpe mig til at løse lignende problemer i fremtiden?

Strategier til løsning af ordproblemer

Det er helt sikkert nyttigt at have en proces til at gribe ordproblemer an. Men vi kan ikke foregive, at man lærer meningsfuld matematik ved blot at følge trin. Hele pointen med ordproblemer er at udvide matematikken ud over “matematiske fakta” og algoritmer.

Der er nogle nyttige strategier til at hjælpe eleverne med at formulere. I begyndelsen underviser jeg eksplicit i en række forskellige strategier.

Når jeg underviser i strategierne, lader jeg eleverne løse opgaver, der passer godt til den pågældende strategi. Nogle problemtyper går rigtig godt sammen med ‘Gæt og tjek’. Andre egner sig bedre til ‘Tegn et billede’.

Eventuelt giver jeg dem udfordrende ordproblemer, som kan løses på flere måder. Når de først har værktøjerne i deres værktøjsbælte, kan de vælge, hvilken der er bedst til situationen.

Kombination af strategier kan også være meget effektiv. For eksempel kan det ofte være nyttigt at tegne et billede for at hjælpe med formuleringen. Hvis en landmand har 18 rækker med gulerødder og 10 gulerødder i hver række, kan en elev starte med at tegne marken. På et tidspunkt tænker de måske “Wow, det er et array” og indser, at de kan gange ved hjælp af mental matematik, et udtryk eller en algoritme.

Andre gange kan eleverne bruge visuelle modeller til at formulere og løse problemet.

Hjælpe dine elever med at tackle udfordrende ordproblemer

Hvis du er som mange lærere, er du måske bekymret for, hvordan dine elever vil håndtere alt dette. Processer, strategier, kritisk tænkning … der er meget involveret.

Du tænker måske endda, at ordproblemer virkede lettere før denne artikel. Hvis det er tilfældet, undskylder jeg.

Nøglen er ikke at blive overvældet af at forsøge at gøre alting på én gang. Start med at løse et simpelt ordproblem ved hjælp af Polya’s proces. Indfør derefter en ny strategi hver uge. Når året er omme, vil du blive overrasket over, hvor langt de er nået.

Måske er du interesseret i at gå dybere ind i kreativ problemløsning. Overvej at deltage i en praktisk matematikworkshop eller at arbejde med en online coach.

Hvis du er klar til at bringe noget Polya ind i dit klasseværelse i morgen, er dette grafiske organizer en god måde at starte på. Det vil give dig et stillads til den fire-trins proces og hjælpe dig med at identificere, hvor dine elever går af sporet.

Gratis ordproblemorganizer

Om forfatteren

Jeff Lisciandrello er grundlægger af Room to Discover og uddannelseskonsulent med speciale i elevcentreret læring. Hans 3-Bridges Design for Learning hjælper skoler med at udforske innovativ praksis inden for traditionelle rammer. Han nyder at hjælpe pædagoger med at omfavne undersøgelsesbaserede og personlige tilgange til undervisning. Du kan komme i kontakt med ham via Twitter @EdTechJeff