Indledning
På denne side gennemgås kontinuitetsligningen, som fremtvinger bevarelse af masse i en eulersk analyse. Dette er ikke strengt taget en beskrivelse af materialeadfærd, men den resulterende ligning anvendes ofte som en identitet til toalgebraisk manipulation af konstitutive modeller, der beskriver materialeadfærd. Det er derfor værd at gennemgå den. Den er også central for analysen af væskestrømning, fordi klassiske væskeanalyser ikke kan være lagrangeanske, da positionerne for alle væskepartiklerne ved \(t = 0\) er ukendte.
Massebevarelse
Kontinuitetsligningen afspejler det faktum, at massen er bevaret i enhver ikke-nuklear kontinuumsmekanisk analyse. Ligningen udvikles ved at addere den hastighed, hvormed massen flyder ind og ud af et kontrolvolumen, og sætte netto-indstrømningen lig med masseændringshastigheden i volumenet. Dette er vist i figuren nedenfor.
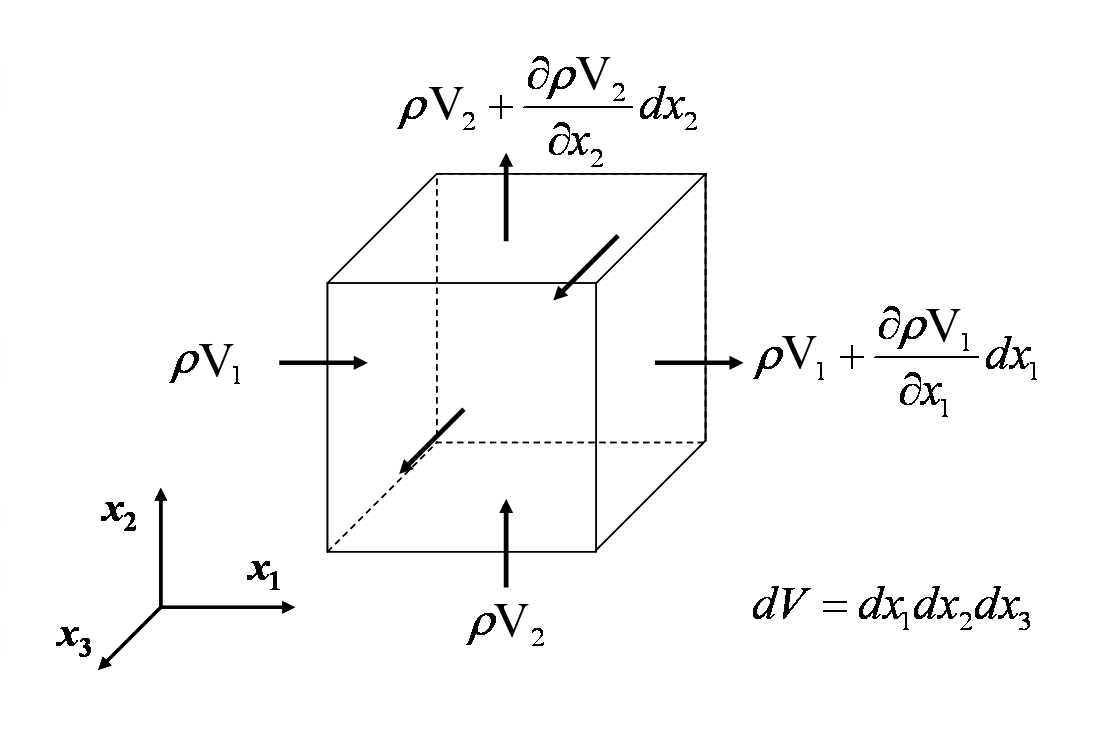
Geligning af alle massestrømningshastighederne ind og ud af det differentielle kontrolvolumen giver
\
Kan man annullere termerne og dividere med \(dx_1 dx_2 dx_3\) giver
\
og omlægning giver
\
Dette kan kortfattet skrives som
\

Vigtige punkter
Dette er de sidste, fuldstændige og mest generelle former af den kontinuitetsligning, der fremtvinger bevarelse af masse. Den gælder for alle materialer, ikke kun for væsker. Så den gælder også for faste stoffer. Bemærk, at det er en enkelt skalarligning og er eulersk i sin natur, fordi gradienttermerne er \({\partial \over \partial x_i}\) og ikke \({\partial \over \partial X_i}\).
Man kan undre sig over, om der findes en lagrangsk pendant til den eulerske form af dette. Det er der. Den skrives normalt som
\
Dette siger simpelthen, at massens differentialkumme i den deformerede tilstand\(\rho \, dV\) skal være lig med dens oprindelige værdi\(\rho_o dV_o\) i den ikke-deformerede tilstand.
Der er flere specialtilfælde af kontinuitetsligningen.Det første forekommer, når strømningen er stationær tilstand. I dette tilfælde er den afledte med hensyn til tidennul, hvorved.
\
Det andet specialtilfælde er det tilfælde, hvor der er inkompressibilitet, dvs, \(\rho = \)konstant.I dette tilfælde er den tidsmæssige afledning nul, og \(\rho\) kan udgå af ligningen, så der kun er
Dette resultat er så simpelt, at det ofte uddybes.
Bemærk, at dette ikke er andet end \(\text{tr}({\bf D}) = 0\) for tilfældet med inkompressible materialer.

Materialeafledning
Det følgende er værd at påpege, fordi det gør det muligt at adskille tætheds- og hastighedsvektorerne. Det første skridt er at anvende produktreglen på divergensudtrykket i kontinuitetsligningen.
\
Og bemærk derefter, at\({{\partiel \rho \over \partiel t} + {\bf v} \cdot \nabla \rho\)blot er den materielle afledning af tætheden,\({D \rho \over D t}\).
Så kontinuitetsligningen kan også skrives som
\
Hvis materialet er inkompressibelt, så kan \(\rho\) ikke ændre sig, så\( {D \rho \over D t} \) må være nul, så
\
Og divider derefter gennem med \(\rho\) (da den ikke er nul) for at få
\

Kontinuitetsligning Eksempel
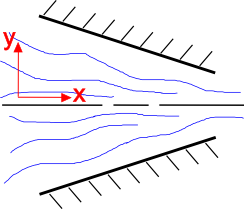
Det er intuitivt, at væskestrømningen accelererer, når tværsnitsarealet mindskes, som vist til højre. Kontinuitetsligningen forklarer dette. Betragt et 2-dimensionalt, stationært strømningsfelt af en inkompressibel væske. kontinuitetsligningen for denne situation er
\
Start med at se på y-komponenten af strømningen, \(v_2\). Geometrien af den konvergerende dyse tvinger \(v_2\) komponenten til at strømme opad, når\(y \lt 0\) og nedad, når \(y \gt 0\). Så \(v_2 \gt 0\) når\(y \lt 0\) og \(v_2 \lt 0\) når \(y \gt 0\).
Nettoeffekten af dette er, at \({\partial v_2 \over \partial x_2} \lt 0\) i den konvergerende dyse.
Men kontinuitetsligningen foreskriver, at summen af de to partielle afledte skal være lig med nul. Så hvis den anden er mindre end nul, så
\
og det betyder, at væskestrømmen må være accelererende.