Konkav vs. konveks?

Hvad er forskellen på konkav og konveks?

Hvis vi skulle beskrive forskellen mellem konkav og konveks på den mest generelle måde, ville vi sige, at ethvert hult, skållignende objekt er konkavt, mens ethvert objekt, der ligner en rugbybold eller en fodbold, har en konveks form. Men måske er grunden til, at konvekse og konkave former så ofte bliver misbrugt, at de to ord ikke er så enkle, som vi gerne vil have dem til at være.

De fleste grammatikkilder insisterer på, hvordan det er muligt at bruge mnemoteknik til at afkode konvekse og konkave gennem ordhulen. Mens forestillingen om at associere konkav med begivenheden, at noget “huler ind”, hjælper med at lære om overfladeegenskaber, er det forvirrende at relatere denne idé til emner, der involverer grafer.

For at forstå, hvordan konkav og konveks er forskellige fra hinanden, er vi nødt til at lære, hvordan hvert udtryk bruges i egenskab af matematik, spejle, linser og endelig inden for kreativ skrivning. Når du først har besluttet dig for, i hvilken sammenhæng du gerne vil bruge ord som konkav og konveks, vil du, hvis du lærer om deres tekniske aspekter, være mere sikker på at bruge dem i daglig tale.

Hvad betyder konkav?

Konkav bruges som adjektiv eller substantiv til at beskrive formen af en genstand eller overflade, der er buet indad eller udhulet som en skål. Eksempler på konkav i en sætning er bl.a.

“Hun skovlede isen fra beholderen og efterlod et konkavt fodaftryk.”

Ifølge The Oxford Dictionary of Word Histories stammer ordet konkav fra sent middelengelsk. Concave og concavity gengiver det latinske begreb concavus (con- og cavus), som kan oversættes til ‘sammen’ og ‘hul’ (“Concave”, 110).

Synonymer til konkav er bl.a.:

Den er indbøjet, nedtrykt, skæv, hul, indbøjet, fordybet og forsænket.

Antonymer af konkav er bl.a.:

Bule, kammeret, fremspringende, udstående, fremspringende, fremspringende, fremspringende.

Hvad betyder konveks?

Ordet konvekse, eller konveksitet, er et adjektiv, der beskriver en genstand eller en overflade, der er afrundet eller buet. Med hensyn til genstande er den midterste overflade af en konveks genstand bredere end dens yderste hjørne. Eksempler på konvekse i en sætning omfatter,

“Jeg faldt ned i giftig efeu og har nu røde, konvekse buler over hele min hud.”

Synonymer for konveks er bl.a.:

Bøjede, bøjede, udbulende, hævede.

Antonymer af konveks er bl.a:

Dykket, nedtrykt, synkende.

Konkave vs. konvekse funktioner

En konveks funktion repræsenterer en kontinuerlig linje på en graf, hvor midtpunktet, eller medianen heltal i et domæne, ikke overstiger intervallets middelværdi. En konkav funktion er det stik modsatte af en konveks funktion, for for at f(x) kan være konkav, skal f(x) være negativ. For at gøre forskellene mere tydelige er her en hurtig gennemgang af, hvordan begreberne sammenlignes:

Konkav opad = konveks = konveks nedad

Konkav nedad = konkav = konveks opad

Skellen mellem konkave og konvekse funktioner fremgår tydeligere, hvis vi ser på en graf. Læg mærke til, hvordan den konvekse funktion åbner opad, mens den konkave funktion åbner nedad.

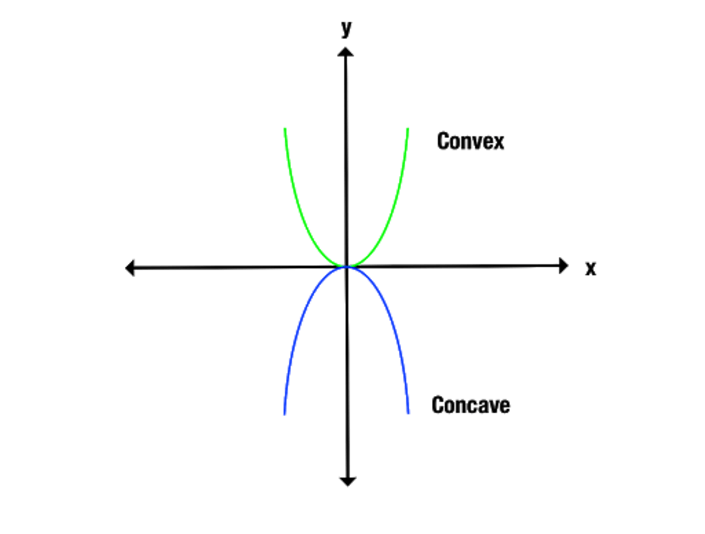
En anden måde at identificere konkave og konvekse funktioner på er ved at forbinde punkter på grafen langs x-aksen. En konkav funktion forbinder kun linjer under grafen, mens en konveks funktion kun giver linjer over grafen.

Vi kan desuden bruge regnearket til at afkode, om en funktion er konveks eller konkav eller ej. Hvis den anden afledte af f(x) er større end nul, så er funktionen konveks. Men hvis den anden afledede af f(x) er mindre end nul, så er funktionen konkav.

Konvekse vs. konkave polygoner

Du skal ikke gå i panik, men ordene konvekse og konkave bruges også i geometri. Konvekse og konkave former diskuteres oftest med henvisning til polygoner, som er figurer med mindst tre sider og vinkler.

Regulære polygoner findes med lige store sider og vinkler, men konvekse og konkave polygoner er en smule mere komplicerede. Konvekse polygoner indeholder indvendige vinkler, der er mindre end 180 grader, mens konkave polygoner indeholder en eller flere indvendige vinkler, der er større end 180 grader.

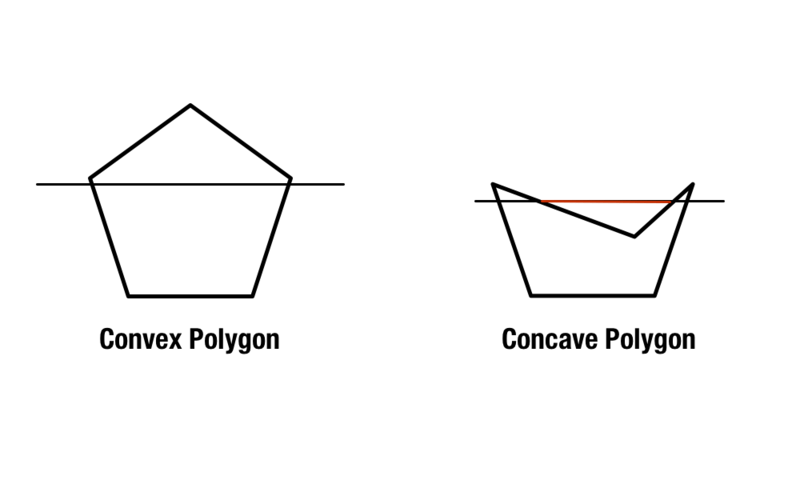
En anden metode til at identificere konkave og konvekse polygoner er at tegne to diagonale linjer på tværs af formen med udgangspunkt i figurens hjørner. Hvis hver linje findes inden for formen, er formen konveks. Hvis der er mindst én linje, der krydser uden for formen, er den konkav.

Konkave vs. konvekse spejle

Ordene konkave og konvekse bruges ofte, når man taler om optiske genstande, f.eks. spejle og linser. Enhver konveks overflade vil rage udad, svarende til en boble, hvilket giver effekten af bredden. Konvekse spejle findes ofte i parkeringshuse, hvor bilisterne har brug for et bredt udsyn omkring hjørner eller potentielle blinde vinkler.

Men i modsætning hertil er et konkavt spejl buet indad og giver et forstørret spejlbillede, der er opadvendt. Som vist af University of South Wales’ School of Physics kan enhver, der har en skinnende ske, teste denne observation ved at se på sit spejlbillede i skeen. På skeens konkave overflade, hvor du tager din mad op, bliver dit spejlbillede forvrænget på en snæver måde, og du vil fremstå på hovedet. Men hvis du vender skeen om til den konvekse side, vil dit spejlbillede være oprejst og mindre.

Refleksioner varierer så meget mellem konvekse og konkave overflader, fordi spejlet i sig selv er en del af en kugle, uanset om overfladen krummer udad eller indad eller ej. Fordi overfladen af en kugle ikke er flad, vil det lys, der reflekteres fra dens overflade, tilbagelægge forskellige afstande, før det kommer i kontakt med spejlet.

Afhængigt af, hvilket område af overfladen lyset kommer i kontakt med, kan en lysstråle reflekteres af nærliggende overflader for at skabe et mere fokuseret synligt område. Det er derfor, at man, når man ser på indersiden af en ske, måske kun ser refleksionen af det, der er tættest på skeens overflade – selv om den stadig ser mindre ud. Hvis man derudover placerer sin finger inde i skeen, kan spejlets overflade frembringe to eller tre forskellige refleksioner på samme tid.

Konkav linse vs. konveks linse

Konkave og konvekse linser findes i dagligdags genstande som f.eks. briller, kontaktlinser, kikkerter og teleskoper. På samme måde som videnskaben bag lysets refleksion på konvekse og konkave spejle findes der også mønstre for, hvordan lys passerer gennem konkave og konvekse linser for at frembringe et synligt billede.

Konvekse linser

Ifølge Manocha Academy kaldes konvekse linser for konvergerende linser, fordi de kan producere billeder, der er formindskede, forstørrede eller indadvendte. Hvor nøjagtigt et billede vises gennem den konvekse linse afhænger af, hvor tæt genstanden er på objektivets brændpunkt. For enhver konveks linse er der symmetriske brændpunkter på hver side af linsen.

Hvor nøjagtigt et objekt fremstilles gennem en konveks linse forudsiges med tre principper:

Princip 1: Enhver lysstråle, der passerer gennem en konveks linse, er parallel med hovedaksen, som er en midterlinje, der går gennem det absolutte centrum af en sfærisk linse. Når lyset kommer i kontakt med linsen, brydes det og passerer gennem brændpunktet på den anden side. Forbipasserende lysstråler, der er parallelle med hovedaksen, bevæger sig over objektet foran linsen.

Princip 2: Enhver lysstråle, der passerer gennem centrum af en konveks linse, fortsætter i en lige linje på den anden side.
Princip 3: Enhver lysstråle, der passerede gennem et brændpunkt på samme side som objektet, vil brydes ved kontakt med linsen og blive parallel med hovedaksen på den anden side.

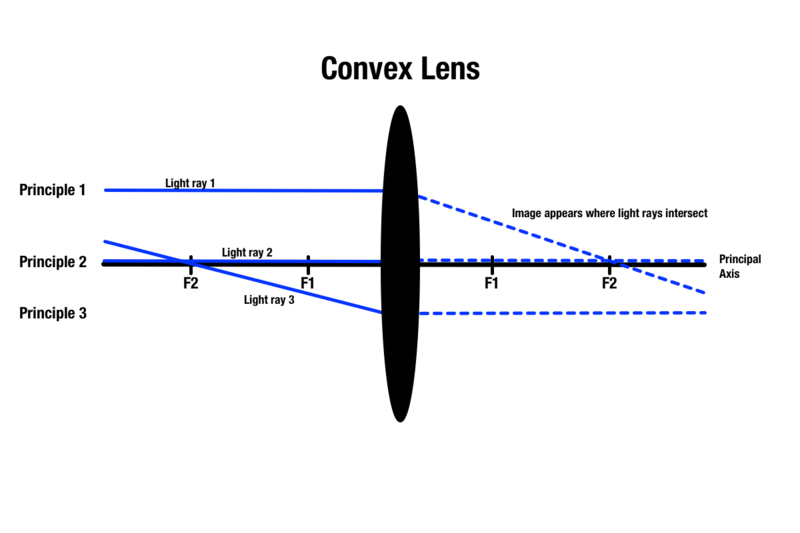
Mens der er tre principper til forudsigelse af billedkvaliteten gennem en konveks linse, kan kun to principper anvendes på et objekt, når man tegner et strålediagram. Enhver to principper vil give et lyskryds på den anden side af linsen, hvilket vil angive det område, hvor objektets billede vises.

Jo længere væk et objekt er fra en konveks linse, jo mindre vil billedet være på den anden side, og jo tættere et objekt er på den konvekse linse, jo større vil det fremstå. Et objekt, der befinder sig forbi det nærmeste brændpunkt, giver et større billede bag objektet. Som Manocha Academy påpeger, anvendes denne type linsestørrelse til optiske redskaber såsom forstørrelsesglas.

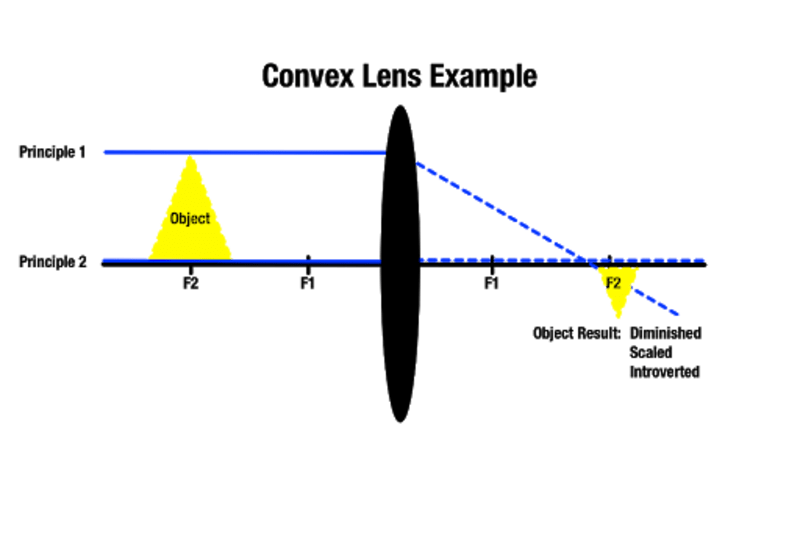
Afhængigt af, hvilket brændpunkt et objekt befinder sig i, er det muligt at frembringe et billede, der er tilnærmelsesvis stort. Det er også muligt at skabe reelle billeder, som ikke er synlige, hvis de forbipasserende lysstråler aldrig skærer hinanden, fordi de er parallelle på den anden side. I dette tilfælde eksisterer det producerede billede i en uendelig afstand.

Konkave linser

Alle konkave linser vil have en tykkere diameter og et tyndere centrum, da en konkav linse er buet indad. Formen på konkave linser gør det muligt for lyset at sprede sig, når det kommer i kontakt med linsen, hvilket får virtuelle objekter til at fremstå mindre. Den konkave linses evne til at sprede lyset gør den til en ideel linse til redskaber som f.eks. lommelygter, hvor en central lyskilde kan bruges over et større område.

Konkave linser producerer billeder med tre principper, der svarer til konvekse linser:

Princip 1: Enhver lysstråle, der bevæger sig over objektet og parallelt med hovedaksen, vil brydes ved kontakt med linsen og fremstå som om den kommer fra retningen af det nærmeste brændpunkt.

Princip 2: Enhver lysstråle, der passerer gennem midten af den konkave linse, vil passere igennem uden at blive brydet.
Princip 3: Enhver lysstråle, der er rettet mod et brændpunkt på den anden side af den konkave linse, vil brydes og blive parallel med hovedaksen.

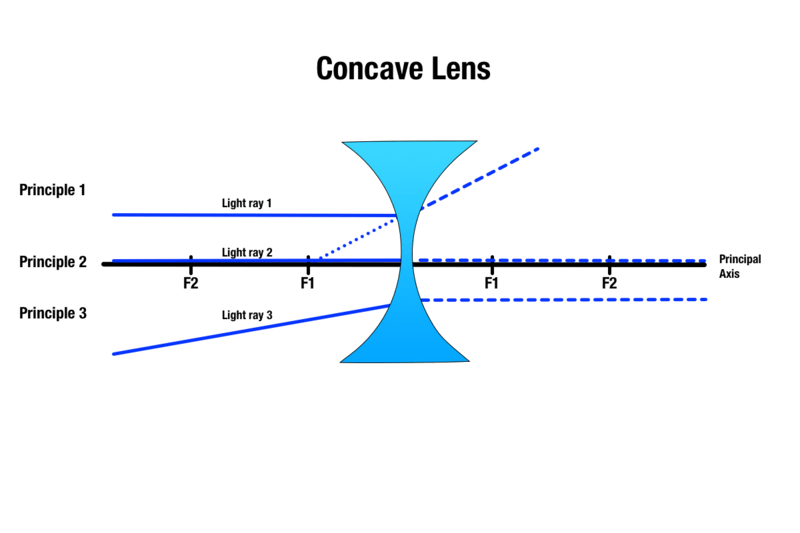
Mens størrelsen af objektets billede vil variere afhængigt af objektets afstand fra en konkav linse, er det producerede billede altid virtuelt, opadrettet, mindre og vises på samme side af linsen som objektet.

Konkav vs. konveks i skrift

Ordene konkav og konveks står i modsætning til hinanden, og de beskriver i det væsentlige formen af genstande eller overflader på samme måde, som vi kontrasterer ord som:

• Små vs. stor
• Lang vs. kort
• Slank vs. bred
• Rund vs. flad

Da konkave og konvekse er tekniske ord, kan brugen af dem beskrivende til prosa give en mere metaforisk eller abstrakt fortolkning for et tilfældigt publikum. Det betyder, at hvis skribenter beslutter sig for at bruge konkave eller konvekse uden for deres typiske anvendelsesområde, skal skribenten beslutte, hvor klart han/hun ønsker at gøre sin tekst tydelig.

Tænk på adjektivet

Et fremtrædende eksempel på brug af konkav eller konveks i litteraturen er at se på den amerikanske forfatter David Foster Wallaces (eller DFW forkortet) forfatterskab. DFW er berygtet for sin komplekse og tekniske skrivestil – og ja, han har flere gange brugt konvekse og konkave til at beskrive navneord. Wallace bruger konkave og konvekse i følgende eksempler:

“Mit håndelaug var okay, men jeg var hverken stor eller hurtig, havde et næsten konkavt bryst og håndled så tynde, at jeg kunne armbinde dem med en tommelfinger og en lillefinger …”

– “Tennis, Trigonometri, Tornadoer: A Midwestern Boyhood,” Harper’s Magazine.

“…dukkeøjne, der åbner sig med et træk i en hjertesnor, konkave, hvor jeg er konveks.”

– “Order and Flux in Northampton,” Conjunctions.

Pointen med at bruge DFW-eksempler er ikke blot at vise, hvordan forfattere har brugt konvekse eller konkave uden for matematisk sammenhæng, men snarere, at forfattere skal overveje, om det er nyttigt at bruge tekniske eller abstrakte udtryk for at kommunikere klart til deres publikum.
I det første DFW-eksempel giver brugen af konkav mening, fordi han beskriver strukturen af noget. Men at bruge konkave og konvekse til at beskrive ikke-objektive navneord, som f.eks. følelser eller tanker, har en tendens til at sløre betydningen af det, vi forsøger at forklare. Det andet DFW-eksempel bevæger sig på en hårfin linje, mens det bruger konvekse og konkave, fordi deres brug er både bogstavelig og metaforisk.

FAQ:

Hvad er en funktion?

En funktion er ligningen for en linje på en graf. Funktioner er forskellige for hver linje på en graf, men de har den generelle form,

f(x) = x + 1

Med enhver linjefunktion er den afhængige variabel typisk f(x), mens enhver ukendt variabel inden for funktionen kaldes en uafhængig variabel.

Hvad er domænet?

Domænet er et sæt af uafhængige variabler på en graf, der svarer til en liniefunktion. Domæner er vigtige at forstå, fordi de lokaliserer specifikke punkter på grafen, der svarer til ethvert reelt output af en ligning.

Hvad er intervallet?

Alle funktionsintervaller repræsenterer enhver mulig værdi langs x- eller y-aksen på en graf, som giver en gyldig værdi for den afhængige variabel. Alle minimale og maksimale hele tal identificeres ved at erstatte x- eller y-aksen med variabler.

Hvad er et interval?

Et interval er et sæt af tal, der repræsenterer de hele tal på en linje, også kaldet domænet. Et lukket interval omfatter to endeløse punkter på en linje, hvor linjen ikke længere eksisterer uden for et heltalsområde. Et åbent interval er et sæt af heltal, der ikke repræsenterer den absolutte ende af en linjes domæne.

Test dig selv!

Se, hvor godt du forstår forskellen mellem konveks og konkav med følgende multiple choice-spørgsmål:

1. Mens du kigger på en skinnende ske, bemærker du, at dit spejlbillede er vendt på hovedet. Skeens overflade er en _________ overflade.
   a. Konveks
   b. Spejl
   c. Konkav
   d. Metal
2. Med hensyn til grafiske funktioner kaldes en konveks funktion nogle gange for:
   a. Konkav opad
   b. Konveks nedad
   c. Konkav nedad
   d. A og B
3. Hvilken af følgende beskriver ikke en konkav overflade:
   a. Hul halvkugle
   b. Øjenlinse
   c. Kornskål
   d. Halvkugle
4. Hvilken af følgende beskriver ikke en konveks overflade:
   a. Karakteren Stewie fra Family Guy
   b. Kugle
   c. Parkeringsgaragespejl
   d. Fodbold
5. Hvilken af følgende figurer kan ikke eksistere som en konkav polygon:
   a. Pentagon
   b. Hexagon
   c. Triangel
   d. Ottekant

Svar

1. C: Konkav
2. D: A og B
3. D: Halvkugle
4. B: Kugle
5. C: Trekant

Kilder:

1. Bourne, M. “Domain and Range of a Function.” Interactive Mathematics, 4. januar 2019.

“Concave.” Merriam-Webster Dictionary, 2019.

2. “Konkav.” The Oxford Dictionary of Word Histories, Ed. Chantrell, 2002, s. 110.
3. “Konkave og konvekse spejle.” Manocha Academy, YouTube, 2019.
4. “Konkav linse: Definition & Anvendelser.” Study.com, 2019.
5. “Konveks.” Merriam-Webster Dictionary, 2019.
6. “Konvekse og konkave linser.” Manocha Academy, YouTube, 2019.
7. “Matematik / Forståelse af polygoner.” Learnhive Inc., 2018.
8. “Refleksion fra et konkavt spejl.” UNSW Physics, YouTube, 2017.
9. Wallace, D.F. “Tennis, trigonometri, tornadoer: A Midwestern Boyhood.” Harper’s Magazine, 1991.
10. Wallace, D.F. “Order and Flux in Northampton.” Conjunctions, 1991.
11. Weisstein, Eric W. “Concave Function.” MathWorld-A Wolfram Web Resource, n.d.

Weisstein, Eric W. “Convex Function.” MathWorld-A Wolfram Web Resource, n.d.

The Word Counter er et dynamisk online værktøj, der bruges til at tælle ord, tegn, sætninger, afsnit og sider i realtid, sammen med stave- og grammatikkontrol.