Indledende erhvervsstatistik

Overvej følgende datasæt.
4; 5; 6; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7; 7; 7; 7; 8; 8; 8; 8; 9; 10

Dette datasæt kan repræsenteres ved følgende histogram. Hvert interval har en bredde på én, og hver værdi er placeret i midten af et interval.

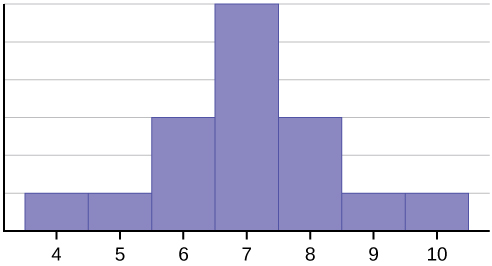
Histogrammet viser en symmetrisk fordeling af data. En fordeling er symmetrisk, hvis der kan trækkes en lodret linje et sted i histogrammet, således at formen til venstre og til højre for den lodrette linje er spejlbilleder af hinanden. Middelværdien, medianen og modus er hver syv for disse data. I en perfekt symmetrisk fordeling er middelværdien og medianen den samme. Dette eksempel har én modus (unimodal), og modus er den samme som middelværdien og medianen. I en symmetrisk fordeling, der har to modes (bimodal), ville de to modes være forskellige fra middelværdien og medianen.

Histogrammet for dataene: 4566677778 er ikke symmetrisk. Højre side virker “hakket af” i forhold til venstre side. En fordeling af denne type kaldes skævt til venstre, fordi den er trukket ud til venstre. Vi kan formelt måle skævheden af en fordeling på samme måde som vi matematisk kan måle dataenes centervægt eller deres generelle “speadness”. Den matematiske formel for skævhed er: . Jo større afvigelsen fra nul er, desto større er skævheden. Hvis skævheden er negativ, er fordelingen skæv til venstre som i (figur). Et positivt mål for skævhed angiver skævhed til højre som i (figur).

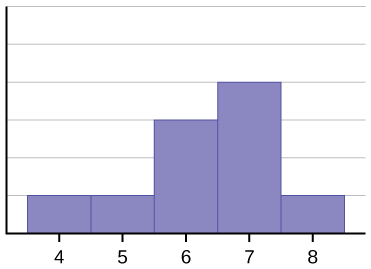
Middelværdien er 6,3, medianen er 6,5, og modus er syv. Bemærk, at middelværdien er mindre end medianen, og at de begge er mindre end modus. Middelværdien og medianen afspejler begge skævheden, men middelværdien afspejler den i højere grad.

Histogrammet for dataene: 67777888910, er heller ikke symmetrisk. Det er skævt til højre.

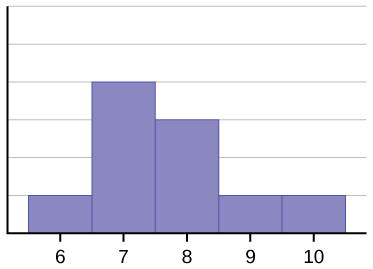
Middelværdien er 7,7, medianen er 7,5, og modus er syv. Af de tre statistikker er middelværdien den største, mens modus er den mindste. Igen afspejler gennemsnittet skævheden mest.

Som opsummering kan man sige, at hvis fordelingen af data generelt er skæv til venstre, er gennemsnittet mindre end medianen, som ofte er mindre end modus. Hvis fordelingen af data er skæv til højre, er modus ofte mindre end medianen, som er mindre end middelværdien.

Som med middelværdien, medianen og modus, og som vi vil se om lidt, variansen, findes der matematiske formler, der giver os præcise mål for disse karakteristika ved fordelingen af dataene. Hvis vi igen ser på formlen for skævhed, kan vi se, at dette er et forhold mellem dataenes gennemsnit og de enkelte observationer sat i tern.

hvor er stikprøvens standardafvigelse for dataene, , og er det aritmetiske gennemsnit og er stikprøvens størrelse.

Formelt set er det aritmetiske gennemsnit kendt som det første moment i fordelingen. Det andet moment, som vi vil se, er variansen, og skævhed er det tredje moment. Variansen måler dataenes kvadrerede forskelle fra middelværdien, og skewness måler dataenes kubiske forskelle fra middelværdien. Mens variansen aldrig kan være et negativt tal, kan skævhedsmålet være det, og det er på denne måde, vi afgør, om dataene er skæve til højre eller venstre. Skævheden for en normalfordeling er nul, og alle symmetriske data bør have en skævhed tæt på nul. Negative værdier for skævhed indikerer data, der er skæve til venstre, og positive værdier for skævhed indikerer data, der er skæve til højre. Med skævt til venstre menes, at den venstre hale er lang i forhold til den højre hale. Tilsvarende betyder skævt til højre, at den højre hale er lang i forhold til den venstre hale. Skævheden karakteriserer graden af asymmetri i en fordeling omkring dens gennemsnit. Mens middelværdien og standardafvigelsen er dimensionelle størrelser (det er derfor, vi tager kvadratroden af variansen ), dvs. har samme enheder som de målte størrelser , er skævheden konventionelt defineret på en sådan måde, at den er ikke-dimensionel. Det er et rent tal, der kun karakteriserer fordelingens form. En positiv værdi af skewness betyder en fordeling med en asymmetrisk hale, der strækker sig ud mod mere positive X, og en negativ værdi betyder en fordeling, hvis hale strækker sig ud mod mere negative X. Et mål på nul for skewness vil indikere en symmetrisk fordeling.

Skewness og symmetri bliver vigtige, når vi diskuterer sandsynlighedsfordelinger i senere kapitler.