Når data er klar til at blive analyseret, bør det vurderes grundigt, baseret på inspektion af dataene, om der bør anvendes statistiske metoder til håndtering af manglende data. Bell et al. havde til formål at vurdere omfanget og håndteringen af manglende data i randomiserede kliniske forsøg, der blev offentliggjort mellem juli og december 2013 i BMJ, JAMA, Lancet og New England Journal of Medicine . 95 % af de 77 identificerede forsøg rapporterede nogle manglende udfaldsdata. Den mest anvendte metode til håndtering af manglende data i den primære analyse var komplet case-analyse (45 %), enkelt imputering (27 %), modelbaserede metoder (f.eks. blandede modeller eller generaliserede estimerende ligninger) (19 %) og multipel imputering (8 %) .
Complete case-analyse
Complete case-analyse er en statistisk analyse baseret på deltagere med et komplet sæt af udfaldsdata. Deltagere med manglende data er udelukket fra analysen. Som beskrevet i indledningen vil den komplette case-analyse, hvis de manglende data er MCAR, have en reduceret statistisk styrke som følge af den reducerede stikprøvestørrelse, men de observerede data vil ikke være skævvredet . Når de manglende data ikke er MCAR, kan den komplette case-analyses estimat af interventionseffekten være baseret, dvs. at der ofte vil være risiko for overvurdering af fordelene og undervurdering af skaderne . Se afsnittet “Bør multipel imputation anvendes til at håndtere manglende data?” for en mere detaljeret diskussion af den potentielle validitet, hvis den komplette case-analyse anvendes.
Single imputation
Ved anvendelse af single imputation erstattes manglende værdier med en værdi, der er defineret af en bestemt regel . Der findes mange former for enkelt imputering, f.eks. sidste observation fremført (en deltagers manglende værdier erstattes af deltagerens sidst observerede værdi), værste observation fremført (en deltagers manglende værdier erstattes af deltagerens værste observerede værdi) og simpel middelimputering . Ved simpel gennemsnitsimputation erstattes manglende værdier med gennemsnittet for den pågældende variabel . Anvendelse af simpel imputation resulterer ofte i en undervurdering af variabiliteten, fordi hver uobserveret værdi har samme vægt i analysen som de kendte, observerede værdier . Validiteten af single imputation afhænger ikke af, om dataene er MCAR; single imputation afhænger snarere af specifikke antagelser om, at de manglende værdier f.eks. er identiske med den sidst observerede værdi . Disse antagelser er ofte urealistiske, og single imputation er derfor ofte en potentielt skæv metode og bør anvendes med stor forsigtighed .
Multiple imputation
Multiple imputation har vist sig at være en gyldig generel metode til håndtering af manglende data i randomiserede kliniske forsøg, og denne metode er tilgængelig for de fleste typer af data . Vi vil i de følgende afsnit beskrive, hvornår og hvordan multipel imputation bør anvendes.
Bør multipel imputation anvendes til håndtering af manglende data?
Grunde til, at multipel imputation ikke bør anvendes til håndtering af manglende data
Er det gyldigt at ignorere manglende data?
Analyse af observerede data (komplet case-analyse), hvor man ignorerer de manglende data, er en gyldig løsning under tre omstændigheder.
- a)
Complete case analysis kan anvendes som primær analyse, hvis andelen af manglende data er under ca. 5 % (som en tommelfingerregel), og det er usandsynligt, at visse patientgrupper (f.eks. de meget syge eller de meget ‘raske’ deltagere) specifikt går tabt til opfølgning i en af de sammenlignede grupper . Med andre ord, hvis den potentielle virkning af de manglende data er ubetydelig, kan der ses bort fra de manglende data i analysen . I tvivlstilfælde kan der anvendes følsomhedsanalyser for det bedste og værste tilfælde: Først genereres et datasæt for det “bedste og værste tilfælde”, hvor det antages, at alle deltagere, der er gået tabt til opfølgning i den ene gruppe (benævnt gruppe 1), har haft et gunstigt resultat (f.eks. ingen alvorlige uønskede hændelser), og at alle deltagere med manglende resultater i den anden gruppe (gruppe 2) har haft et skadeligt resultat (f.eks. har haft en alvorlig uønsket hændelse) . Derefter genereres et datasæt for det værst mulige scenarie, hvor det antages, at alle deltagere, der er gået tabt til opfølgning i gruppe 1, har haft et skadeligt resultat, og at alle deltagere, der er gået tabt til opfølgning i gruppe 2, har haft et gavnligt resultat . Hvis der anvendes kontinuerlige resultater, kan et “gavnligt resultat” være gruppens gennemsnit plus 2 standardafvigelser (eller 1 standardafvigelse) af gruppens gennemsnit, og et “skadeligt resultat” kan være gruppens gennemsnit minus 2 standardafvigelser (eller 1 standardafvigelse) af gruppens gennemsnit . For dikotomiserede data vil disse følsomhedsanalyser for det værste og værste tilfælde vise usikkerhedsintervallet på grund af manglende data, og hvis dette interval ikke giver kvalitativt modstridende resultater, kan der ses bort fra de manglende data. For kontinuerte data vil en imputering med 2 SD repræsentere et muligt usikkerhedsinterval givet 95 % af de observerede data (hvis de er normalfordelte).
- b)
Hvis kun den afhængige variabel har manglende værdier, og der ikke er identificeret hjælpevariabler (variabler, der ikke indgår i regressionsanalysen, men som er korreleret med en variabel med manglende værdier og/eller er relateret til dens manglende værdier), kan en komplet case-analyse anvendes som den primære analyse, og der bør ikke anvendes særlige metoder til at håndtere de manglende data. Der vil ikke blive opnået yderligere oplysninger ved f.eks. at anvende multiple imputation, men standardfejlene kan stige på grund af den usikkerhed, der indføres ved den multiple imputation .
- c)
Som nævnt ovenfor (se Metoder til håndtering af manglende data) vil det også være gyldigt blot at foretage en komplet case-analyse, hvis det er relativt sikkert, at dataene er MCAR (se Indledning). Det er relativt sjældent, at det er relativt sikkert, at dataene er MCAR. Det er muligt at teste hypotesen om, at dataene er MCAR med Little’s test , men det kan være uklogt at bygge videre på tests, der viste sig at være insignifikante. Hvis der er rimelig tvivl om, hvorvidt dataene er MCAR, selv om Little’s test er insignifikant (ikke kan forkaste nulhypotesen om, at dataene er MCAR), bør MCAR derfor ikke antages.
Er andelen af manglende data for stor?
Hvis store andele af data mangler, bør det overvejes blot at rapportere resultaterne af den fuldstændige caseanalyse og derefter klart diskutere de deraf følgende fortolkningsmæssige begrænsninger af forsøgsresultaterne. Hvis der anvendes multiple imputationer eller andre metoder til at håndtere manglende data, kan det antyde, at forsøgets resultater er bekræftende, hvilket de ikke er, hvis der mangler en stor del af dataene. Hvis andelen af manglende data er meget stor (f.eks. mere end 40 %) for vigtige variabler, kan forsøgsresultaterne kun betragtes som hypotesegenererende resultater . En sjælden undtagelse vil være, hvis den underliggende mekanisme bag de manglende data kan beskrives som MCAR (se afsnit ovenfor)
Er MCAR- og MAR-antagelsen begge usandsynlige?
Hvis MAR-antagelsen forekommer usandsynlig på baggrund af de manglende datas karakteristika, vil forsøgsresultaterne være i risiko for fordrejede resultater på grund af “ufuldstændige udfaldsdata bias”, og ingen statistisk metode kan med sikkerhed tage højde for denne potentielle bias . Validiteten af de metoder, der anvendes til at håndtere MNAR-data, kræver visse antagelser, som ikke kan testes på grundlag af observerede data. Følsomhedsanalyser af de bedste og værst mulige tilfælde kan vise hele det teoretiske usikkerhedsområde, og konklusionerne bør relateres til dette usikkerhedsområde. Analysernes begrænsninger bør diskuteres og overvejes grundigt.
Er udfaldsvariablen med manglende værdier kontinuerlig, og er den analytiske model kompliceret (f.eks. med interaktioner)?
I denne situation kan man overveje at anvende den direkte maximum likelihood-metode for at undgå problemerne med modelkompatibilitet mellem den analytiske model og den multiple imputeringsmodel, hvor førstnævnte er mere generel end sidstnævnte. Generelt kan man anvende direkte maximum likelihood-metoder, men så vidt vides er kommercielt tilgængelige metoder på nuværende tidspunkt kun tilgængelige for kontinuerte variabler.
Hvornår og hvordan man skal anvende multiple imputationer
Hvis ingen af “Årsagerne til, at multiple imputationer ikke bør anvendes til at håndtere manglende data” fra ovenfor er opfyldt, kan man anvende multiple imputationer. I litteraturen er der i de sidste årtier blevet foreslået forskellige procedurer til håndtering af manglende data . Vi har skitseret de ovennævnte overvejelser om statistiske metoder til håndtering af manglende data i fig. 1.
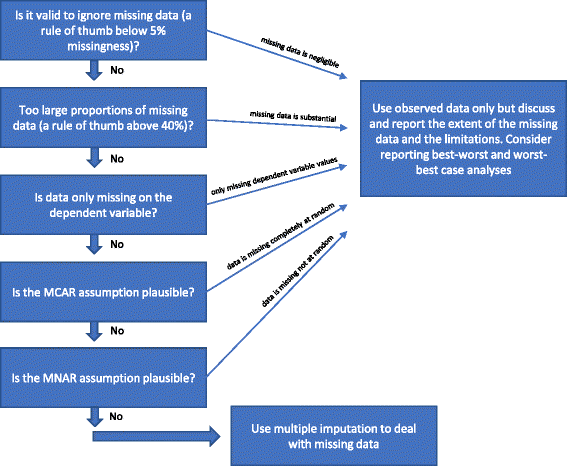
Flowchart: Hvornår bør multipel imputation anvendes til at håndtere manglende data ved analyse af resultater af randomiserede kliniske forsøg
Multipel imputation stammer fra begyndelsen af 1970’erne og har vundet stigende popularitet i årenes løb . Multiple imputation er en simulationsbaseret statistisk teknik til håndtering af manglende data . Multiple imputation består af tre trin:
-
Imputationstrin. En “imputation” repræsenterer generelt ét sæt plausible værdier for manglende data – multipel imputation repræsenterer flere sæt plausible værdier . Ved brug af multipel imputation identificeres manglende værdier og erstattes af en tilfældig stikprøve af imputationer af plausible værdier (fuldstændige datasæt). Der genereres flere komplette datasæt ved hjælp af en valgt imputeringsmodel . Fem imputerede datasæt er traditionelt blevet foreslået som værende tilstrækkeligt af teoretiske grunde, men 50 datasæt (eller flere) synes at være at foretrække for at reducere stikprøvevariabiliteten fra imputeringsprocessen .
-
Fuldstændige dataanalyse (estimation) trin. Den ønskede analyse udføres separat for hvert datasæt, der genereres i forbindelse med imputeringsprocessen . Herved konstrueres der f.eks. 50 analyseresultater.
-
Pooling-trin. De resultater, der er opnået fra hver afsluttet dataanalyse, kombineres til et enkelt resultat af flere imputeringer . Der er ikke behov for at foretage en vægtet metaanalyse, da alle f.eks. 50 analyseresultater anses for at have samme statistiske vægt.
- 1)
Det er nemmere at implementere, dvs. det er ikke nødvendigt at gennemgå forskellige trin som ved brug af multiple imputation
- 2)
I modsætning til multiple imputation har full information maximum likelihood ingen potentielle problemer med inkompatibilitet mellem imputationsmodellen og analysemodellen (se “Multiple imputation”). Validiteten af resultaterne af den multiple imputering vil være tvivlsom, hvis der er en inkompatibilitet mellem imputeringsmodellen og analysemodellen, eller hvis imputeringsmodellen er mindre generel end analysemodellen .
- 3)
Ved anvendelse af multipel imputation erstattes alle manglende værdier i hvert genereret datasæt (imputationstrin) med en tilfældig stikprøve af plausible værdier . Medmindre der er angivet “a random seed”, vil der derfor blive vist forskellige resultater, hver gang der udføres en analyse med flere imputeringer, medmindre der er angivet “a random seed” . Analyser ved anvendelse af full information maximum likelihood på det samme datasæt vil give de samme resultater hver gang analysen udføres, og resultaterne er derfor ikke afhængige af en random number seed . Hvis den tilfældige seed-værdi defineres i den statistiske analyseplan kan dette problem dog løses.
-
Vi har allerede beskrevet brugen af best-worst- og worst-best case-følsomhedsanalyser til at vise intervallet af usikkerhed som følge af manglende data (se Vurdering af, om der bør anvendes metoder til håndtering af manglende data). Vores tidligere beskrivelse af best-worst- og worst-best case-følsomhedsanalyser var relateret til manglende data om enten en dikotomisk eller en kontinuert afhængig variabel, men disse følsomhedsanalyser kan også anvendes, når der mangler data om stratificeringsvariabler, baselineværdier osv. Den potentielle indflydelse af manglende data bør vurderes for hver variabel for sig, dvs. der bør være et best-worst- og et worst-best case-scenarie for hver variabel (afhængig variabel, resultatindikator og stratificeringsvariabler) med manglende data.
-
Hvis det besluttes, at der f.eks. skal anvendes multiple imputationer, bør disse resultater være det primære resultat af det givne resultat. Hver primær regressionsanalyse bør altid suppleres med en tilsvarende observeret (eller tilgængelig) case-analyse.
Det er af stor betydning, at der enten er kompatibilitet mellem imputeringsmodellen og analysemodellen, eller at imputeringsmodellen er mere generel end analysemodellen (f.eks. at imputeringsmodellen omfatter flere uafhængige kovariater end analysemodellen) . Hvis analysemodellen f.eks. har signifikante interaktioner, bør imputeringsmodellen også omfatte dem , hvis analysemodellen anvender en transformeret version af en variabel, bør imputeringsmodellen anvende den samme transformation osv.
Differente typer af multipel imputering
Der findes forskellige typer af metoder til multipel imputering. Vi vil præsentere dem i henhold til deres stigende grad af kompleksitet: 1) regressionsanalyse med enkeltværdi; 2) monotonisk imputation; 3) kædeformede ligninger eller Markov-kæde Monte Carlo-metoden (MCMC). Vi vil i de følgende afsnit beskrive disse forskellige multiple imputeringsmetoder, og hvordan man vælger mellem dem.
En regressionsanalyse med en enkelt variabel omfatter en afhængig variabel og de stratificeringsvariabler, der er anvendt i randomiseringen. Stratificeringsvariablerne omfatter ofte en centerindikator, hvis forsøget er et multicenterforsøg, og normalt en eller flere justeringsvariable med prognostiske oplysninger, som er korreleret med resultatet. Når der anvendes en kontinuert afhængig variabel, kan der også medtages en baselineværdi for den afhængige variabel. Som nævnt i “Årsager til, at statistiske metoder ikke bør anvendes til at håndtere manglende data” bør der, hvis kun den afhængige variabel har manglende værdier, og der ikke er identificeret hjælpevariabler, foretages en fuldstændig case-analyse, og der bør ikke anvendes særlige metoder til at håndtere de manglende data. Hvis der er identificeret hjælpevariabler, kan der foretages en imputation af en enkelt variabel. Hvis der er betydelige mangler på basisvariablen for en kontinuert variabel, kan en komplet case-analyse give skæve resultater . Derfor foretages der under alle omstændigheder en imputering med en enkelt variabel (med eller uden ekstra variabler inkluderet efter behov), hvis kun basisvariablen mangler.
Hvis både den afhængige variabel og basisvariablen mangler, og manglen er monoton, foretages der en monoton imputering. Antag en datamatrix, hvor patienterne er repræsenteret ved rækker og variablerne ved kolonner. Manglen på en sådan datamatrix siges at være monoton, hvis kolonnerne kan omarrangeres således, at for enhver patient a) hvis en værdi mangler, mangler alle værdier til højre for denne værdi også, og b) hvis en værdi er observeret, er alle værdier til venstre for denne værdi også observeret. Hvis den manglende værdi er monoton, er metoden til multipel imputering også relativt ligetil, selv om mere end én variabel har manglende værdier . I dette tilfælde er det relativt enkelt at imputere de manglende data ved hjælp af sekventiel regressionsimputation, hvor de manglende værdier imputeres for hver variabel ad gangen . Mange statistiske pakker (f.eks. STATA) kan analysere, om missingness er monoton eller ej.
Hvis missingness ikke er monoton, foretages en multipel imputering ved hjælp af kædeformede ligninger eller MCMC-metoden. Hjælpevariabler medtages i modellen, hvis de er tilgængelige. Vi har opsummeret, hvordan man vælger mellem de forskellige multiple imputeringsmetoder i fig. 2.
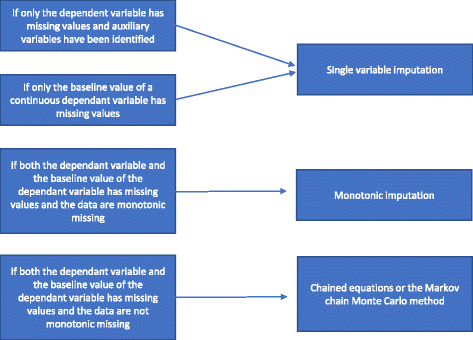
Flowchart over multiple imputering
Full information maximum likelihood
Full information maximum likelihood er en alternativ metode til håndtering af manglende data . Princippet i maximum likelihood-estimation er at estimere parametre for den fælles fordeling af resultatet (Y) og kovariater (X1,…, Xk), som, hvis de var sande, ville maksimere sandsynligheden for at observere de værdier, som vi faktisk observerede . Hvis der mangler værdier for en given patient, kan vi få sandsynligheden ved at summere den sædvanlige sandsynlighed over alle mulige værdier af de manglende data, forudsat at mekanismen for manglende data er ignorabel. Denne metode kaldes full information maximum likelihood .
Full information maximum likelihood har både styrker og begrænsninger i forhold til multiple imputation.
Styrker ved full information maximum likelihood i forhold til multiple imputation
Begrænsninger ved full information maximum likelihood sammenlignet med multiple imputation
Begrænsningerne ved anvendelse af full information maximum likelihood sammenlignet med anvendelse af multiple imputation, er, at anvendelse af full information maximum likelihood kun er mulig ved hjælp af specielt designet software . Der er blevet udviklet foreløbig designet software, men de fleste af disse har ikke de samme funktioner som kommercielt udviklet statistisk software (f.eks. STATA, SAS eller SPSS). I STATA (ved hjælp af SEM-kommandoen) og SAS (ved hjælp af PROC CALIS-kommandoen) er det muligt at anvende full information maximum likelihood, men kun når der anvendes kontinuerlige afhængige (udfalds)variabler. For logistisk regression og Cox-regression er den eneste kommercielle pakke, der giver fuld information maximum likelihood for manglende data, Mplus.
En anden potentiel begrænsning ved anvendelse af fuld information maximum likelihood er, at der kan være en underliggende antagelse om multivariat normalitet . Ikke desto mindre er overtrædelser af den multivariate normalitetsantagelse måske ikke så vigtige, så det kan være acceptabelt at medtage binære uafhængige variabler i analysen.
Vi har i Additional file 1 inkluderet et program (SAS), der producerer et fuldt legetøjsdatasæt, herunder flere forskellige analyser af disse data. Tabel 1 og tabel 2 viser output og viser, hvordan forskellige metoder, der håndterer manglende data, giver forskellige resultater.
Panelværdier regressionsanalyse
Paneldata er normalt indeholdt i en såkaldt bred datafil, hvor den første række indeholder variabelnavnene, og de efterfølgende rækker (én for hver patient) indeholder de tilsvarende værdier. Resultatet repræsenteres af forskellige variabler – en for hver planlagt, tidsbestemt måling af resultatet. For at analysere dataene skal filen konverteres til en såkaldt lang fil med én post pr. planlagt måling af udfaldet, herunder udfaldsværdien, tidspunktet for målingen og en kopi af alle andre variabelværdier undtagen værdierne for udfaldsvariablen. For at bevare korrelationerne inden for patienten mellem de tidsbestemte resultatmålinger er det almindelig praksis at foretage en multipelimputering af datafilen i dens brede form efterfulgt af en analyse af den resulterende fil, efter at den er blevet konverteret til dens lange form. Proc mixed (SAS 9.4) kan anvendes til analyse af kontinuerlige udfaldsværdier og proc. glimmix (SAS 9.4) til andre typer af udfald. Da disse procedurer anvender den direkte maximum likelihood-metode på udfaldsdataene, men ignorerer tilfælde med manglende covariatværdier, kan procedurerne anvendes direkte, når der kun mangler værdier af afhængige variabler, og der ikke er gode hjælpevariabler til rådighed. I modsat fald bør proc. mixed eller proc. glimmix (alt efter hvad der er relevant) anvendes efter en multipel beregning. Det er klart, at en tilsvarende fremgangsmåde kan være mulig ved hjælp af andre statistiske pakker.
Følsomhedsanalyser
Følsomhedsanalyser kan defineres som et sæt analyser, hvor data håndteres på en anden måde end i den primære analyse. Følsomhedsanalyser kan vise, hvordan antagelser, der adskiller sig fra de antagelser, der er gjort i den primære analyse, påvirker de opnåede resultater . Følsomhedsanalyser bør være foruddefineret og beskrevet i den statistiske analyseplan, men yderligere post hoc-følsomhedsanalyser kan være berettigede og gyldige. Når den potentielle indflydelse af manglende værdier er uklar, anbefaler vi følgende følsomhedsanalyser:
Når der anvendes blandede effektmetoder
Det vil ofte være nødvendigt at anvende et multicenterforsøgsdesign for at rekruttere et tilstrækkeligt antal forsøgsdeltagere inden for en rimelig tidsramme . Et multicenterforsøgsdesign giver også et bedre grundlag for den efterfølgende generalisering af resultaterne . Det er blevet vist, at de mest almindeligt anvendte analysemetoder i randomiserede kliniske forsøg fungerer godt med et lille antal centre (analyse af binært afhængige resultater) . Med et relativt stort antal centre (50 eller flere) er det ofte optimalt at anvende “center” som en tilfældig effekt og at anvende analysemetoder med blandede effekter. Det vil ofte også være hensigtsmæssigt at anvende analysemetoder med blandede effekter, når der analyseres longitudinelle data . Det kan under visse omstændigheder være hensigtsmæssigt at medtage kovariatet med “tilfældig effekt” (f.eks. “center”) som en kovariat med fast effekt under imputationstrinnet og derefter anvende blandede modeller eller generaliserede estimerende ligninger (GEE) under analysetrinnet . Anvendelsen af en model med blandede effekter (med f.eks. “center” som en tilfældig effekt) indebærer imidlertid, at der skal tages hensyn til dataenes flerlagede struktur ved modelleringen af den multiple imputering. Nu er der ikke direkte kommerciel software til rådighed til at gøre dette. Man kan dog anvende REALCOME-pakken, som kan kobles sammen med STATA . Grænsefladen eksporterer data med manglende værdier fra STATA til REALCOM, hvor imputeringen foretages under hensyntagen til dataenes flerniveaukarakter og ved hjælp af en MCMC-metode, der omfatter kontinuerte variabler og ved hjælp af en latent normal model også giver mulighed for en korrekt håndtering af diskrete data . De imputerede datasæt kan derefter analyseres ved hjælp af STATA-kommandoen “mi estimate:”, som kan kombineres med erklæringen “mixed” (for et kontinuert resultat) eller erklæringen “meqrlogit” for et binært eller ordinalt resultat i STATA . Ved analyse af paneldata kan man imidlertid let komme ud for en situation, hvor dataene omfatter tre eller flere niveauer, f.eks. målinger inden for den samme patient (niveau-1), patienter inden for centre (niveau-2) og centre (niveau-3) . For ikke at blive involveret i en ret kompliceret model, som kan føre til manglende konvergens eller ustabile standardfejl, og som der ikke findes kommerciel software til, vil vi anbefale, at man enten behandler centereffekten som fast (direkte eller efter sammenlægning af små centre til et eller flere centre af passende størrelse ved hjælp af en procedure, der skal foreskrives i den statistiske analyseplan) eller udelukker centeret som en kovariabel. Hvis randomiseringen er blevet stratificeret efter center, vil sidstnævnte fremgangsmåde føre til en opadgående skævhed i standardfejlene, hvilket resulterer i en noget konservativ testprocedure .