Som med kage kan du have 2 små stykker eller 1 stykke, der er dobbelt så stort, og det er den samme mængde. Derfor er en masse brøker ækvivalente, som f.eks. 2/5 og 4/10.


Alt tal kan skrives som et brøk
Skriv ethvert helt tal over 1 for at gøre det til et brøk, da det samlede antal dele i ethvert uopdelt helt tal er 1.
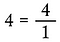
Multiplikér brøker lige på tværs
Det er nemt at multiplicere brøker, du skal bare gange lige på tværs.
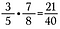
Bemærk: Blandede tal skal først omdannes til ukorrekte brøker, læs mere om dette.
Multiplikér med enhver form for 1 til enhver tid
Tallet 1 kaldes den multiplikative identitet, fordi vi kan multiplicere det med et hvilket som helst tal, og tallet forbliver det samme. Dette er vigtigt for brøker, fordi vi ofte har brug for at ændre udseendet af en brøk uden faktisk at ændre dens værdi.
For eksempel kan jeg ændre 1/3 til den tilsvarende brøk 3/9 ved at gange med 3/3.
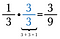
Addér og subtraher lige store dele
Når man adderer og subtraherer brøker, skal nævnerne være de samme. Det giver god mening. Hvis vi vil kombinere eller fjerne dele, skal der være tale om dele af samme størrelse, ellers bliver det forvirrende.
Så hvad gør du, hvis dine brøker ikke har samme størrelse?
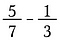
Multiplikér med en form af et for at ændre nævnerne til en fælles størrelse. I bund og grund deler vi brøkerne op i mindre store stykker, indtil de er af samme størrelse. Dette kaldes at finde en fællesnævner.
Sandt nok kan enhver fællesnævner bruges, men folk foretrækker at finde den mindste. I dette tilfælde er det mindste tal, som både 7 og 3 går ind i uden en rest, 21. Så gang den første brøk med 3/3 og den anden med 7/7.
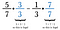
Hvis du ikke kan komme på den mindste fællesnævner, kan du altid gange hver brøk med den modsatte nævner. Nogle gange, som i dette tilfælde, viser det sig at være den mindste fællesnævner. Hvis det ikke er det, skal du bare reducere dit svar til sidst.
Når nævnerne passer sammen, skal du trække tællerne fra hinanden for at få 8/21.
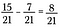
Dette fungerer, som man kunne forvente. Billedligt set begynder man med 15 stykker af i alt 21.

Fjern farven fra 7 af de 15 blå klodser.

Hvilket giver 8/21 som forventet.
Skift først blandede tal ud
Et blandet tal er kombinationen af et helt tal og en brøk.
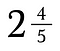
Blandede tal spiller ikke godt sammen med andre brøker. Det er en god idé at omdanne dem til ukorrekte brøker først.
Bemærk: En ukorrekt brøk er en brøk, hvis tæller er større end dens nævner og derfor har en værdi større end 1.
Omdannelse af et blandet tal er egentlig addition
For at omdanne 2 og 4/5 til en ukorrekt brøk skal du tilføje 2 + 4/5.
Strin 1: Begynd med at omskrive 2 til 2/1.
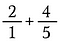
Stræk 2: Multiplicer 2/1 med 5/5 for at lave en tilsvarende brøk på 10/5, som har den ønskede fællesnævner på 5.
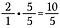
Stræk 3: Læg 10/5 + 4/5 sammen.
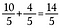
Vores resultat er den tilsvarende ulige brøk 14/5.
For at konvertere tilbage til et blandet tal udfører du divisionen. For eksempel går 5 ind i 14 to gange (da 5 x 2 = 10) med 4 stykker tilbage.
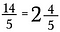
Sammenlign brøker ved hjælp af krydsproduktet
Sæt, at vi vil bestemme, hvilket brøk der er størst: 5/12 eller 6/13.
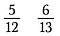
Strap et: Multiplicer en diagonal, og skriv produktet over tælleren.
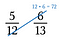
Stræk to: Multiplicer den anden diagonal, og skriv dens produkt over tælleren.
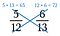
Stræk tre: Sammenlign produkterne. Den side med det største produkt er den største brøk. Så i dette tilfælde er 5/12 mindre end 6/13.
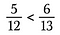
Vi kan også bestemme, om brøker er lige store ved hjælp af krydsprodukter.
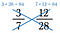
Krydsningsproduktet af 3/7 og 12/28 er begge 84, derfor er 3/7 = 12/28.
Annuller alt, der dividerer til et
Det bedste ved brøker er, at man kan finde masser af muligheder for at annullere. Hvilket gør dem hurtige og nemme at håndtere.
Sæt, at jeg har brøken 8/10. Både 8 og 10 kan omskrives med 2 som faktor.
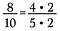
Da 2/2 = 1, kan jeg annullere 2’eren, så jeg får 4/5 tilbage som den reducerede brøk.
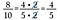
Udnyt denne strategi til også at gøre det lettere at gange brøker.
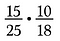
Begynd med at omskrive hvert tal i faktorer.
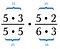
Slet alle talpar, der dividerer til 1. F.eks. 5/5 = 1.
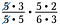
Jeg har endnu et par 5’ere samt et par 3’ere, der også dividerer til 1.
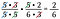
Ops! Jeg kunne have omskrevet 6 som 2 x 3 og annulleret et par 2’ere. Det er okay, hvis du mangler en faktor, bare fortsæt, indtil du får dem alle.
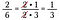
Hvis jeg havde ganget 15/25 gange 10/18 direkte ville det have været en masse aritmetik, ved at bruge annullering forreducerer jeg brøkerne på forhånd og gør det enklere at gange.
Brug multiplikation til at dividere brøker
Begrebet om at dividere brøker er nemt med enkle eksempler som:

Der er to halvdele i en hel, derfor er der 10 halvdele i 5 helheder.
Men begrebet bliver vanskeligere med mere komplicerede brøker.
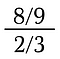
For at løse dette problem vil vi benytte os af to kendsgerninger:
- Vi kan gange med enhver form for et (i.dvs. alt over sig selv)
- Multiplikation med den reciprokke af 3/2, som er 2/3, resulterer i 1 via annullering
Strin et:
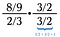
Nu har vi to mindre problemer at løse (blå og grøn).
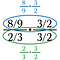
Skridt to: Annuller alt, der dividerer til 1 i den nederste (grønne) brøk. Det skal altid give 1.

Nu er vi tilbage med det øverste problem, som vi skal løse.
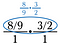
Strin tre: Brug annullering til at reducere brøken på forhånd. Når du har foretaget disse reduktioner, skal du gange på tværs for at få 4/3.

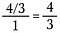
Kortvej
Dette er den lange hånd mekanik af “vend og multiplicer”.”
Vi kan springe multiplikation med det reciprokke i bunden over, da det altid annullerer til 1. Derfor skal du blot gange tælleren med det reciprokke af nævneren.

Bonus: Teori, hvis du er interesseret…
Godt spørgsmål! For at generalisere kan du lave to brøker ved at bruge bogstaverne a, b, c og d til at repræsentere fire forskellige tal.
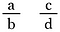
Multiplicer begge brøker med b-d (på den måde kan vi ophæve nævnerne).
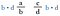
Nu annullerer vi b’erne til venstre og d’erne til højre, da de dividerer til 1. Vi har ikke længere brøker, kun produkterne d-a og c-b.
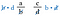
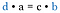
Kig tilbage på de oprindelige brøker. Det er de samme produkter, som hvis vi havde ganget diagonalerne. Derfor er genvejen at sammenligne krydsproduktet.
❤ BLIVER FORBINDET ❤
Hold dig opdateret med alt, hvad Math Hacks har gang i!