Grafteori – typer af grafer

Der findes forskellige typer af grafer afhængigt af antallet af hjørner, antallet af kanter, sammenkoblingsmuligheder og deres overordnede struktur. Vi vil kun diskutere nogle få vigtige typer grafer i dette kapitel.

Nulgraf

En graf uden kanter kaldes en nulgraf.

Eksempel

I ovenstående graf er der tre toppunkter ved navn ‘a’, ‘b’ og ‘c’, men der er ingen kanter mellem dem. Derfor er det en nulgraf.

Trivialgraf

En graf med kun ét toppunkt kaldes en trivialgraf.

Eksempel

I den ovenfor viste graf er der kun ét toppunkt ‘a’ uden andre kanter. Derfor er det en Trivial graf.

Non-directed Graph

En non-directed graf indeholder kanter, men kanterne er ikke dirigerede.

Eksempel

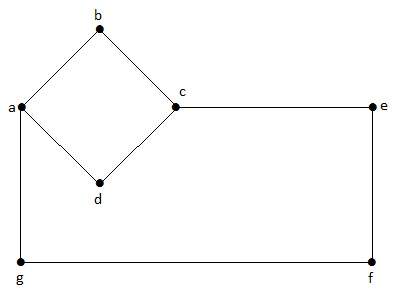
I denne graf er ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’ toppene, og ‘ab’, ‘bc’, ‘cd’, ‘da’, ‘ag’, ‘gf’, ‘ef’ er grafernes kanter. Da det er en ikke-retningsbestemt graf, er kanterne “ab” og “ba” ens. Tilsvarende andre kanter betragtes også på samme måde.

Direkte grafer

I en rettet graf har hver kant en retning.

Eksempel

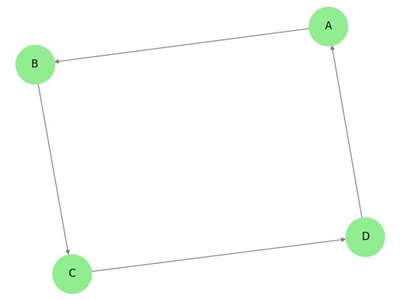
I ovenstående graf har vi syv toppunkter ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’ og ‘g’, og otte kanter ‘ab’, ‘cb’, ‘dc’, ‘ad’, ‘ec’, ‘fe’, ‘gf’ og ‘ga’. Da det er en rettet graf, er hver kant forsynet med et pilmærke, der viser dens retning. Bemærk, at i en rettet graf er ‘ab’ forskellig fra ‘ba’.

En simpel graf

En graf uden sløjfer og uden parallelle kanter kaldes en simpel graf.

• Det maksimale antal mulige kanter i en enkelt graf med ‘n’ hjørner er nC2, hvor nC2 = n(n – 1)/2.

• Det mulige antal simple grafer med ‘n’ hjørner er 2nc2 = 2n(n – 1)/2.

Eksempel

I den følgende graf er der 3 hjørner med 3 kanter, hvilket er maksimalt eksklusive de parallelle kanter og sløjfer. Dette kan bevises ved hjælp af ovenstående formler.

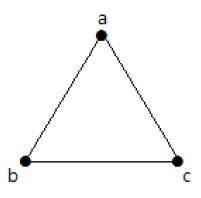
Det maksimale antal kanter med n=3 hjørner –

nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges

Det maksimale antal simple grafer med n=3 hjørner –

2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8

Disse 8 grafer er som vist nedenfor –

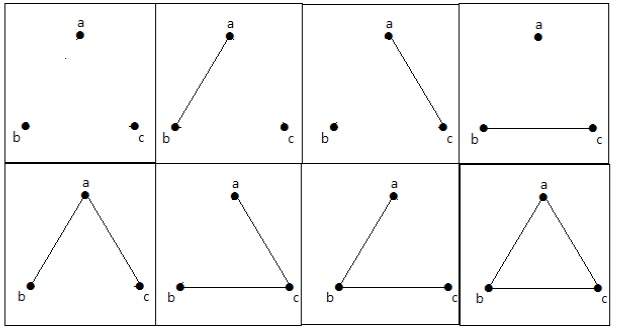
Sammenhængende graf

En graf G siges at være forbundet, hvis der findes en sti mellem hvert par af hjørner. Der skal være mindst én kant for hvert toppunkt i grafen. Så vi kan sige, at det er forbundet med et andet toppunkt på den anden side af kanten.

Eksempel

I den følgende graf har hvert toppunkt sin egen kant forbundet med en anden kant. Derfor er det en sammenhængende graf.

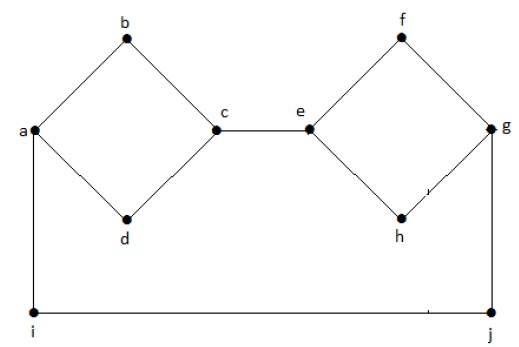
Disconnected Graph

En graf G er disconnected, hvis den ikke indeholder mindst to sammenhængende toppunkter.

Eksempel 1

Den følgende graf er et eksempel på en Disconnected Graph, hvor der er to komponenter, en med ‘a’, ‘b’, ‘c’, ‘d’ toppunkter og en anden med ‘e’, ‘f’, ‘g’, ‘h’ toppunkter.

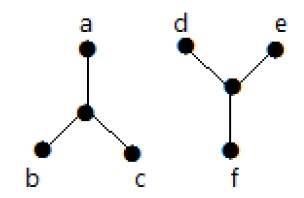
De to komponenter er uafhængige og er ikke forbundet med hinanden. Derfor kaldes den for en usammenhængende graf.

Eksempel 2

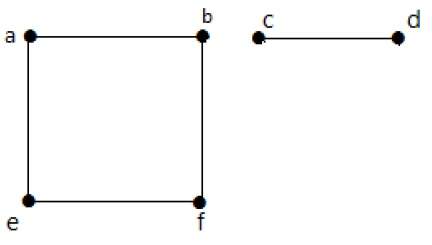
I dette eksempel er der to uafhængige komponenter, a-b-f-e og c-d, som ikke er forbundet med hinanden. Derfor er dette en usammenhængende graf.

Regulær graf

En graf G siges at være regulær, hvis alle dens hjørner har den samme grad. Hvis graden af hvert toppunkt i en graf er “k”, kaldes grafen for en “k-regulær graf”.

Eksempel

I følgende grafer har alle toppene den samme grad. Så disse grafer kaldes regulære grafer.

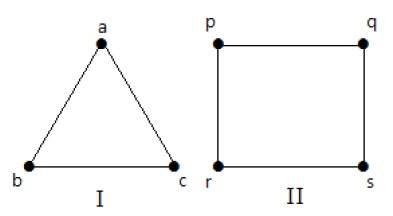
I begge grafer har alle toppene grad 2. De kaldes 2-regulære grafer.

Komplet graf

En simpel graf med ‘n’ gensidige toppunkter kaldes en komplet graf, og den betegnes med ‘Kn’. I grafen skal et toppunkt have kanter med alle andre toppunkter, så kaldes den en komplet graf.

Med andre ord, hvis et toppunkt er forbundet med alle andre toppunkter i en graf, så kaldes den en komplet graf.

Eksempel

I de følgende grafer er hvert toppunkt i grafen forbundet med alle de resterende toppunkter i grafen undtagen med sig selv.

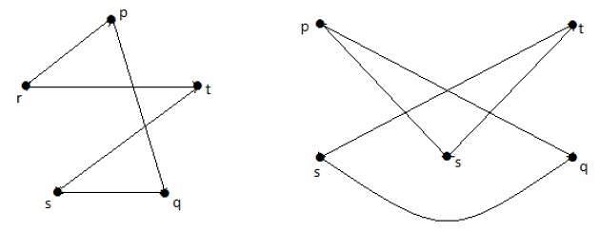
I graf I,

	a	b	c
a	Not Connected	Connected	Connected	Connected
b	Sammenkoblet	Ikke sammenkoblet	Sammenkoblet
c	Sammenkoblet	Sammenkoblet	Ikke sammenkoblet

I graf II,

	p	q	r	s
p	Not Connected	Connected	Connected	Connected	Tilsluttet
q	Tilsluttet	Ikke tilsluttet	Tilsluttet	Tilsluttet	Tilsluttet
r	Tilsluttet	Tilsluttet	Ikke tilsluttet	Tilsluttet
s	Tilsluttet	Tilsluttet	Tilsluttet	Ikke tilsluttet	Ikke Connected

Cykelgraf

En simpel graf med “n” hjørner (n >= 3) og “n” kanter kaldes en cyklusgraf, hvis alle dens kanter danner en cyklus af længde “n”.

Hvis graden af hvert toppunkt i grafen er to, kaldes den en cyklusgraf.

Notation – Cn

Eksempel

Se på følgende grafer –

• Grafen I har 3 toppunkter med 3 kanter, som danner en cyklus ‘ab-bc-ca’.

• Graf II har 4 toppunkter med 4 kanter, som danner en cyklus ‘pq-qs-sr-rp’.

• Graf III har 5 toppunkter med 5 kanter, som danner en cyklus ‘ik-km-ml-lj-ji’.

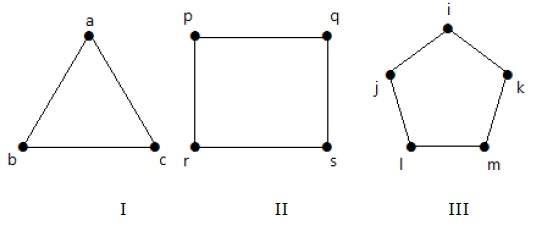
Hermed er alle de givne grafer cyklusgrafer.

Hjulgraf

En hjulgraf fås fra en cyklusgraf Cn-1 ved at tilføje et nyt toppunkt. Dette nye toppunkt kaldes et knudepunkt, som er forbundet med alle toppunkter i Cn.

Notation – Wn

No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)

Eksempel

Se på følgende grafer. De er alle hjulgrafer.

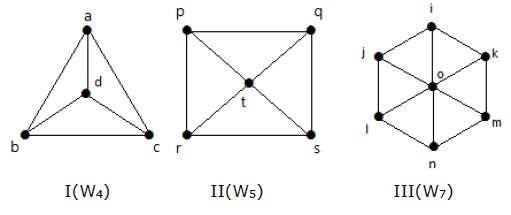
I graf I fås den fra C3 ved at tilføje et toppunkt i midten, der hedder “d”. Den betegnes W4.

Number of edges in W4 = 2(n-1) = 2(3) = 6

I graf II fås den fra C4 ved at tilføje et toppunkt i midten med navnet “t”. Den betegnes som W5.

Number of edges in W5 = 2(n-1) = 2(4) = 8

I graf III fås den fra C6 ved at tilføje et toppunkt i midten med betegnelsen “o”. Den betegnes som W7.

Number of edges in W4 = 2(n-1) = 2(6) = 12

Cyklisk graf

En graf med mindst én cyklus kaldes en cyklisk graf.

Eksempel

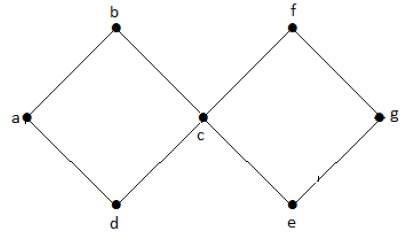
I ovenstående eksempelgraf har vi to cyklusser a-b-c-c-d-a og c-f-g-e-c. Derfor kaldes den en cyklisk graf.

Acyklisk graf

En graf uden cyklusser kaldes en acyklisk graf.

Eksempel

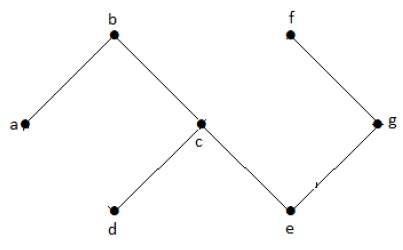
I ovenstående eksempelgraf har vi ikke nogen cyklusser. Derfor er det en ikke-cyklisk graf.

Bipartite grafer

En simpel graf G = (V, E) med toppunktsfordeling V = {V1, V2} kaldes en bipartite graf, hvis hver kant i E forbinder et toppunkt i V1 med et toppunkt i V2.

En bipartitisk graf har generelt to sæt af toppunkter, lad os sige V1 og V2, og hvis der tegnes en kant, skal den forbinde ethvert toppunkt i mængden V1 med ethvert toppunkt i mængden V2.

Eksempel

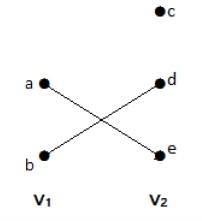
I denne graf kan man iagttage to sæt af toppunkter – V1 og V2. Her forbinder to kanter ved navn “ae” og “bd” toppene i de to sæt V1 og V2.

Komplet bipartite graf

En bipartite graf “G”, G = (V, E) med partition V = {V1, V2} siges at være en komplet bipartite graf, hvis alle toppene i V1 er forbundet med alle toppene i V2.

En komplet bipartit graf forbinder generelt hvert toppunkt fra mængden V1 med hvert toppunkt fra mængden V2.

Eksempel

Den følgende graf er en komplet bipartit graf, fordi den har kanter, der forbinder hvert toppunkt fra mængden V1 med hvert toppunkt fra mængden V2.

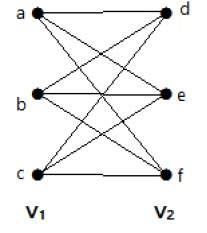
Hvis |V1| = m og |V2| = n, så betegnes den komplette bipartit graf med Km, n.

• Km,n har (m+n) toppunkter og (mn) kanter.

• Km,n er en regulær graf, hvis m=n.

En komplet bipartite graf er generelt ikke en komplet graf.

Km,n er en komplet graf, hvis m=n=1.

Det maksimale antal kanter i en bipartit graf med n toppunkter er

Hvis n=10, k5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25

Sådan er det også med K6, 4=24

K7, 3=21

K8, 2=16

K9, 1=9

Hvis n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20

Sådan er det også med K6, 3=18

K7, 2=14

K8, 1=8

‘G’ er en bipartit graf, hvis ‘G’ ikke har nogen cykler af ulige længde. Et specialtilfælde af en bipartit graf er en stjernegraf.

Stjernegraf

En komplet bipartit graf af formen K1, n-1 er en stjernegraf med n-bjælker. En stjernegraf er en komplet bipartite graf, hvis et enkelt toppunkt hører til det ene sæt, og alle de resterende toppunkter hører til det andet sæt.

Eksempel

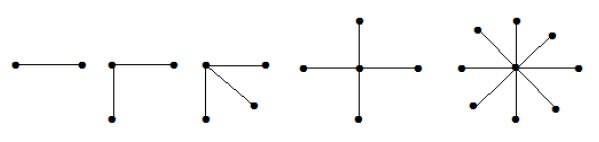
I ovenstående grafer er alle “n-1” toppunkter ud af “n” toppunkter forbundet med et enkelt toppunkt. Derfor er det i form af K1, n-1, som er stjernegrafer.

Komplement af en graf

Lad “G-” være en simpel graf med nogle toppunkter som i “G”, og en kant {U, V} er til stede i “G-“, hvis kanten ikke er til stede i G. Det betyder, at to toppunkter er tilstødende i “G-“, hvis de to toppunkter ikke er tilstødende i G.

Hvis de kanter, der findes i graf I, er fraværende i en anden graf II, og hvis både graf I og graf II kombineres sammen til en komplet graf, kaldes graf I og graf II for komplementer af hinanden.

Eksempel

I følgende eksempel har graf-I to kanter ‘cd’ og ‘bd’. Dens komplement graf-II har fire kanter.

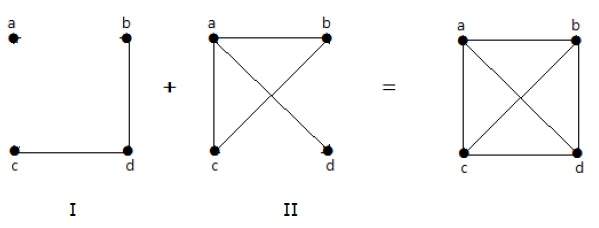
Bemærk, at kanterne i graf-I ikke er til stede i graf-II og omvendt. Kombinationen af begge grafer giver derfor en komplet graf med ‘n’ hjørner.

Bemærk – En kombination af to komplementære grafer giver en komplet graf.

Hvis ‘G’ er en hvilken som helst simpel graf, så

|E(G)| + |E(‘G-‘)| = |E(Kn)|, hvor n = antallet af hjørner i grafen.

Eksempel

Lad ‘G’ være en simpel graf med ni hjørner og tolv kanter, find antallet af kanter i ‘G-‘.

Du har, |E(G)| + |E(‘G-‘)| = |E(Kn)|

12 + |E(‘G-‘)| =