For nylig stillede en af mine kollegaer mig et par spørgsmål som “hvorfor har vi så mange aktiveringsfunktioner?”, “hvorfor er det, at den ene virker bedre end den anden?”, “hvordan ved vi, hvilken funktion vi skal bruge?”, “er det hardcore matematik?” og så videre. Så jeg tænkte, hvorfor ikke skrive en artikel om det for dem, der kun er bekendt med neurale netværk på et grundlæggende niveau og derfor undrer sig over aktiveringsfunktioner og deres “hvorfor-hvorfor-matematik!”.
BEMÆRK: Denne artikel forudsætter, at du har et grundlæggende kendskab til en kunstig “neuron”. Jeg vil anbefale, at du læser op på det grundlæggende om neurale netværk, før du læser denne artikel for at få en bedre forståelse.
Aktiveringsfunktioner
Så hvad gør et kunstigt neuron? Kort sagt beregner den en “vægtet sum” af dens input, tilføjer en bias og beslutter derefter, om den skal “fyres” eller ej ( ja, det er rigtigt, det gør en aktiveringsfunktion, men lad os følge med strømmen et øjeblik ).
Så tænk på en neuron.
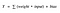
Nu kan værdien af Y være alt fra -inf til +inf. Neuronet kender reelt ikke grænserne for værdien. Så hvordan beslutter vi, om neuronet skal fyre eller ej ( hvorfor dette fyringsmønster? Fordi vi har lært det af biologien, at det er sådan hjernen fungerer, og hjernen er et arbejdsvidnesbyrd om et fantastisk og intelligent system ).
Vi besluttede at tilføje “aktiveringsfunktioner” til dette formål. For at kontrollere den Y-værdi, der produceres af en neuron og beslutte, om eksterne forbindelser skal betragte denne neuron som “fyret” eller ej. Eller lad os snarere sige – “aktiveret” eller ej.
Step-funktion
Det første, der falder os ind, er, hvad med en tærskelværdibaseret aktiveringsfunktion? Hvis værdien af Y er over en bestemt værdi, erklæres den for aktiveret. Hvis den er mindre end tærskelværdien, så siges det, at den ikke er det. Hmm fantastisk. Det kunne fungere!
Aktiveringsfunktion A = “aktiveret” hvis Y tærskelværdi ellers ikke
Alternativt: A = 1 hvis y tærskelværdi, 0 ellers
Jamen, det vi lige har gjort er en “trinfunktion”, se nedenstående figur.
Dets output er 1 ( aktiveret) når værdi 0 (tærskel) og udsender en 0 ( ikke aktiveret) ellers.
Glimrende. Det giver altså en aktiveringsfunktion for en neuron. Ingen forvirringer. Der er dog visse ulemper ved dette. For at forstå det bedre skal du tænke på følgende:
Sæt, at du opretter en binær klassifikator. Noget som skal sige et “ja” eller “nej” ( aktivere eller ikke aktivere ). En Step-funktion kunne gøre det for dig! Det er præcis hvad den gør, siger et 1 eller 0. Tænk nu på den use case hvor du vil have flere sådanne neuroner til at blive forbundet for at få flere klasser ind. Klasse1, klasse2, klasse3 osv. Hvad vil der ske, hvis mere end 1 neuron bliver “aktiveret”. Alle neuroner vil udstede en 1 ( fra trinfunktionen). Hvad ville du nu beslutte? Hvilken klasse er det? Hmm svært, kompliceret.
Du ville ønske at netværket kun aktiverer 1 neuron og de andre skal være 0 ( kun da ville du kunne sige at det klassificerede korrekt/identificerede klassen ). Ah! Det er sværere at træne og konvergere på denne måde. Det ville have været bedre, hvis aktiveringen ikke var binær, og der i stedet stod “50% aktiveret” eller “20% aktiveret” osv. Og så kunne man, hvis mere end 1 neuron aktiveres, finde frem til hvilket neuron der har den “højeste aktivering” osv. ( bedre end max, et softmax, men lad os lade det ligge for nu ).
I dette tilfælde også, hvis mere end 1 neuron siger “100% aktiveret”, er problemet stadigvæk til stede.Jeg ved det! Men..da der er mellemliggende aktiveringsværdier for output, kan læring være glattere og lettere ( mindre wiggly ) og chancerne for at mere end 1 neuron er 100% aktiveret er mindre i forhold til trinfunktion under træning ( også afhængigt af hvad du træner og data ).
Ok, så vi vil have noget til at give os mellemliggende ( analoge ) aktiveringsværdier i stedet for at sige “aktiveret” eller ikke ( binært ).
Det første, der falder os ind, ville være Lineær funktion.
Linær funktion
A = cx
En retlinet funktion, hvor aktiveringen er proportional med input ( som er den vægtede sum fra neuron ).
På denne måde giver den et interval af aktiveringer, så det er ikke binær aktivering. Vi kan helt sikkert forbinde et par neuroner sammen, og hvis mere end 1 fyrer, kan vi tage max ( eller softmax ) og beslutte ud fra det. Så det er også ok. Hvad er så problemet med dette?
Hvis du er bekendt med gradientafstigning til træning, vil du bemærke, at for denne funktion er afledningen en konstant.
A = cx, afledningen i forhold til x er c. Det betyder, at gradienten ikke har nogen sammenhæng med X. Det er en konstant gradient, og afstigningen vil foregå på konstant gradient. Hvis der er en fejl i forudsigelsen, er de ændringer, der foretages af back propagation, konstante og ikke afhængige af ændringen i input delta(x) !!!
Det er ikke så godt! ( ikke altid, men bær over med mig ). Der er også et andet problem. Tænk på forbundne lag. Hvert lag aktiveres af en lineær funktion. Denne aktivering går igen ind i det næste lag som input, og det andet lag beregner vægtet sum på dette input, og det affyrer igen baseret på en anden lineær aktiveringsfunktion.
Og uanset hvor mange lag vi har, hvis alle er lineære i naturen, er den endelige aktiveringsfunktion i det sidste lag ikke andet end blot en lineær funktion af input fra første lag! Hold en lille pause og tænk over det.
Det betyder, at disse to lag ( eller N lag ) kan erstattes af et enkelt lag. Ah! Vi har lige mistet muligheden for at stable lag på denne måde. Uanset hvordan vi stabler, svarer hele netværket stadig til et enkelt lag med lineær aktivering ( en kombination af lineære funktioner på en lineær måde er stadig en anden lineær funktion ).
Lad os komme videre, skal vi?
Sigmoidfunktion
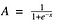
Jamen, det ser glat og “trinfunktionslignende” ud. Hvad er fordelene ved dette? Tænk over det et øjeblik. Først og fremmest er det ikke-lineært i sin natur. Kombinationer af denne funktion er også ikke-lineære! Fint. Nu kan vi stable lag på lag. Hvad med ikke-binære aktiveringer? Ja, også det!. Det vil give en analog aktivering i modsætning til trinfunktion. Den har også en jævn gradient.
Og hvis du lægger mærke til, at mellem X-værdierne -2 til 2, er Y-værdierne meget stejle. Hvilket betyder, at enhver lille ændring i X-værdierne i dette område vil medføre, at værdierne for Y ændres betydeligt. Ah, det betyder, at denne funktion har en tendens til at bringe Y-værdierne til begge ender af kurven.
Det ser ud til, at den er god til en klassifikator i betragtning af dens egenskab? Ja ! Det er den faktisk. Den har en tendens til at bringe aktiveringerne til begge sider af kurven ( over x = 2 og under x = -2 for eksempel). Gør klare sondringer på forudsigelse.
En anden fordel ved denne aktiveringsfunktion er, i modsætning til lineær funktion, at aktiveringsfunktionens output altid vil ligge i intervallet (0,1) sammenlignet med (-inf, inf) for lineær funktion. Så vi har vores aktiveringer bundet i et område. Dejligt, det vil ikke sprænge aktiveringerne så.
Det er godt. Sigmoide funktioner er en af de mest udbredte aktiveringsfunktioner i dag. Hvad er så problemerne med dette?
Hvis du lægger mærke til, at mod begge ender af sigmoidfunktionen har Y-værdierne en tendens til at reagere meget mindre på ændringer i X. Hvad betyder det? Gradienten i dette område vil være lille. Det giver anledning til et problem med “forsvindende gradienter”. Hmm. Hvad sker der så, når aktiveringerne når tæt på den “nær-horisontale” del af kurven på begge sider?
Gradienten er lille eller er forsvundet ( kan ikke foretage væsentlige ændringer på grund af den ekstremt lille værdi ). Netværket nægter at lære yderligere eller er drastisk langsomt ( afhængig af brugssituation og indtil gradient/beregning bliver ramt af grænser for floating point-værdi ). Der er måder at arbejde uden om dette problem på, og sigmoid er stadig meget populær i klassifikationsproblemer.
Tanh-funktion
En anden aktiveringsfunktion, der anvendes, er tanh-funktionen.
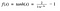
Hm. Det ligner meget sigmoid. Faktisk er det en skaleret sigmoidfunktion!

Ok, nu har dette egenskaber, der ligner sigmoid, som vi diskuterede ovenfor. Den er ikke-lineær i sin natur, så fantastisk vi kan stakke lag! Den er bundet til området (-1, 1), så ingen bekymringer om, at aktiveringer eksploderer. Et punkt at nævne er, at gradienten er stærkere for tanh end sigmoid ( afledninger er stejlere). Beslutningen mellem sigmoid eller tanh vil afhænge af dit krav til gradientstyrke. Ligesom sigmoid har tanh også problemet med forsvindende gradient.
Tanh er også en meget populær og meget anvendt aktiveringsfunktion.
ReLu
Sidst kommer ReLu-funktionen,
A(x) = max(0,x)
ReLu-funktionen er som vist ovenfor. Den giver et output x hvis x er positiv og 0 ellers.
Det ser ved første øjekast ud til at have de samme problemer som en lineær funktion, da den er lineær i positiv akse. For det første er ReLu ikke lineær i sin natur. Og kombinationer af ReLu er også ikke-lineære! ( faktisk er det en god approksimator. Enhver funktion kan tilnærmes med kombinationer af ReLu). Fint, det betyder altså, at vi kan stable lag. Det er dog ikke bundet. ReLu’s område er [0, inf). Det betyder, at den kan sprænge aktiveringen op.
Et andet punkt, som jeg gerne vil diskutere her, er sparsomheden af aktiveringen. Forestil dig et stort neuralt netværk med en masse neuroner. Brug af en sigmoid eller tanh vil få næsten alle neuroner til at fyre på en analog måde ( husker du? ). Det betyder, at næsten alle aktiveringer vil blive behandlet for at beskrive et netværks output. Med andre ord er aktiveringen tæt. Dette er dyrt. Vi vil ideelt set ønske, at nogle få neuroner i netværket ikke aktiveres og dermed gøre aktiveringerne sparsomme og effektive.
ReLu giver os denne fordel. Forestil dig et netværk med tilfældigt initialiserede vægte ( eller normaliserede ), og næsten 50 % af netværket giver 0 aktivering på grund af ReLu’s karakteristik ( output 0 for negative værdier af x ). Det betyder, at færre neuroner affyres ( sparsom aktivering ), og at netværket er lettere. Woah, flot! ReLu ser ud til at være fantastisk! Ja, det er det, men intet er fejlfrit… Ikke engang ReLu.
På grund af den vandrette linje i ReLu ( for negativ X ) kan gradienten gå mod 0. For aktiveringer i det område af ReLu vil gradienten være 0, hvorfor vægtene ikke bliver justeret under nedstigningen. Det betyder, at de neuroner, der går ind i denne tilstand, vil holde op med at reagere på variationer i fejl/ input ( simpelthen fordi gradienten er 0, ændres der intet ). Dette kaldes det døende ReLu-problem. Dette problem kan medføre, at flere neuroner bare dør og ikke reagerer, hvilket gør en væsentlig del af netværket passivt. Der findes variationer i ReLu for at afhjælpe dette problem ved simpelthen at gøre den horisontale linje til en ikke-horisontal komponent . f.eks. y = 0,01x for x<0 vil gøre den til en let skrå linje i stedet for en horisontal linje. Dette er en utæt ReLu. Der findes også andre variationer. Hovedidéen er at lade gradienten være ikke-nul og genoprettes i løbet af træningen til sidst.
ReLu er mindre beregningsmæssigt dyrt end tanh og sigmoid, fordi det indebærer enklere matematiske operationer. Det er et godt punkt at overveje, når vi designer dybe neurale net.
Ok, hvilken skal vi nu bruge?
Nu skal vi finde ud af, hvilke aktiveringsfunktioner vi skal bruge. Betyder det, at vi bare bruger ReLu til alt, hvad vi gør? Eller sigmoid eller tanh? Tja, ja og nej. Når man ved, at den funktion, man forsøger at tilnærme sig, har visse egenskaber, kan man vælge en aktiveringsfunktion, som vil tilnærme sig funktionen hurtigere, hvilket fører til en hurtigere træningsproces. F.eks. fungerer en sigmoid godt til en klassifikator ( se grafen for sigmoid, viser den ikke egenskaberne for en ideel klassifikator? ), fordi det er lettere at tilnærme en klassifikatorfunktion som kombinationer af sigmoide end f.eks. Hvilket vil føre til en hurtigere træningsproces og konvergens. Du kan også bruge dine egne brugerdefinerede funktioner!. Hvis du ikke kender karakteren af den funktion du forsøger at lære, så vil jeg måske foreslå at starte med ReLu, og så arbejde baglæns. ReLu fungerer det meste af tiden som en generel approximator!
I denne artikel har jeg forsøgt at beskrive nogle få aktiveringsfunktioner, der ofte anvendes. Der findes også andre aktiveringsfunktioner, men den generelle idé forbliver den samme. Forskning efter bedre aktiveringsfunktioner er stadig i gang. Jeg håber, at du fik idéen bag aktiveringsfunktionen, hvorfor de bruges, og hvordan vi beslutter, hvilken funktion vi skal bruge.