10.5: Halbleiter – Bandlücken, Farben, Leitfähigkeit und Dotierung

Leitfähigkeit von intrinsischen Halbleitern

Die Leitfähigkeit (σ) ist das Produkt aus der Anzahldichte der Ladungsträger (n oder p), ihrer Ladung (e) und ihrer Beweglichkeit (µ). Aus Kapitel 6 wissen wir, dass µ das Verhältnis zwischen der Ladungsträgerdriftgeschwindigkeit und dem elektrischen Feld ist und die Einheit cm2/Volt-Sekunde hat. Typischerweise haben Elektronen und Löcher etwas unterschiedliche Beweglichkeiten (µe bzw. µh), so dass die Leitfähigkeit gegeben ist durch:

\

Für jeden Ladungsträgertyp ist die Beweglichkeit μ gegeben durch:

\

wobei e die Grundeinheit der Ladung, τ die Streuzeit und m die effektive Masse des Ladungsträgers ist.

Mittelt man die Elektronen- und Lochmobilität und verwendet n = p, so erhält man

\

Durch Messung der Leitfähigkeit in Abhängigkeit von der Temperatur erhält man die Aktivierungsenergie für die Leitung, die Egap/2 ist. Ein solches Diagramm, das einem Arrhenius-Diagramm ähnelt, ist rechts für drei verschiedene undotierte Halbleiter dargestellt. Die Steigung der Linie ist in jedem Fall -Egap/2k.

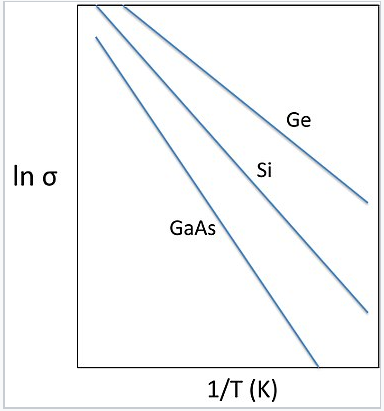
Darstellungen von ln(σ) gegen die inverse Temperatur für die intrinsischen Halbleiter Ge (Egap = 0,7 eV), Si (1,1 eV) und GaAs (1,4 eV). Die Steigung der Linie ist -Egap/2k.

Dotierung von Halbleitern. Fast alle Anwendungen von Halbleitern beinhalten eine kontrollierte Dotierung, d.h. die Substitution von Fremdatomen in das Gitter. Sehr kleine Mengen von Dotierstoffen (im Promillebereich) beeinflussen die Leitfähigkeit von Halbleitern drastisch. Aus diesem Grund werden sehr reine Halbleitermaterialien benötigt, die sowohl hinsichtlich der Konzentration als auch der räumlichen Verteilung der Fremdatome sorgfältig dotiert sind.

n- und p-Typ-Dotierung. In kristallinem Si hat jedes Atom vier Valenzelektronen und geht vier Bindungen mit seinen Nachbarn ein. Dies ist genau die richtige Anzahl von Elektronen, um das Valenzband des Halbleiters vollständig zu füllen. Durch das Einfügen eines Phosphoratoms in das Gitter (das positiv geladene Atom in der Abbildung rechts) wird ein zusätzliches Elektron hinzugefügt, da P fünf Valenzelektronen hat und nur vier benötigt, um Bindungen mit seinen Nachbarn einzugehen. Das zusätzliche Elektron ist bei niedriger Temperatur an das Phosphoratom in einem wasserstoffähnlichen Molekülorbital gebunden, das wegen der hohen Dielektrizitätskonstante des Halbleiters viel größer ist als das 3s-Orbital eines isolierten P-Atoms. In Silizium beträgt dieser „erweiterte“ Bohr-Radius etwa 42 Å, d. h. er ist 80-mal größer als beim Wasserstoffatom. Die Energie, die erforderlich ist, um dieses Elektron zu ionisieren – damit es sich frei im Gitter bewegen kann -, beträgt nur etwa 40-50 meV, was nicht viel mehr ist als die thermische Energie (26 meV) bei Raumtemperatur. Daher liegt das Fermi-Niveau knapp unterhalb der Leitungsbandkante, und ein großer Teil dieser zusätzlichen Elektronen wird bei Raumtemperatur in das Leitungsband befördert, wobei feste positive Ladungen auf den P-Atomstellen zurückbleiben. Der Kristall ist n-dotiert, was bedeutet, dass der Hauptladungsträger (Elektron) negativ geladen ist.

Alternativ kann Bor das Silizium im Gitter ersetzen, was zu einer p-Dotierung führt, bei der der Hauptladungsträger (Loch) positiv geladen ist. Bor hat nur drei Valenzelektronen und „leiht“ sich eines aus dem Siliziumgitter, wodurch ein positiv geladenes Loch entsteht, das sich in einem großen wasserstoffähnlichen Orbital um das B-Atom befindet. Dieses Loch kann delokalisiert werden, indem ein Elektron aus dem Valenzband zum Auffüllen des lokalisierten Lochzustands befördert wird. Auch dieser Prozess erfordert nur 40-50 meV, so dass bei Raumtemperatur ein großer Teil der durch die Bor-Dotierung eingebrachten Löcher in delokalisierten Valenzbandzuständen vorliegt. Das Fermi-Niveau (das Elektronenenergieniveau, das bei Nulltemperatur eine 50%ige Besetzungswahrscheinlichkeit hat) liegt in einem p-Typ-Halbleiter knapp über der Valenzbandkante.

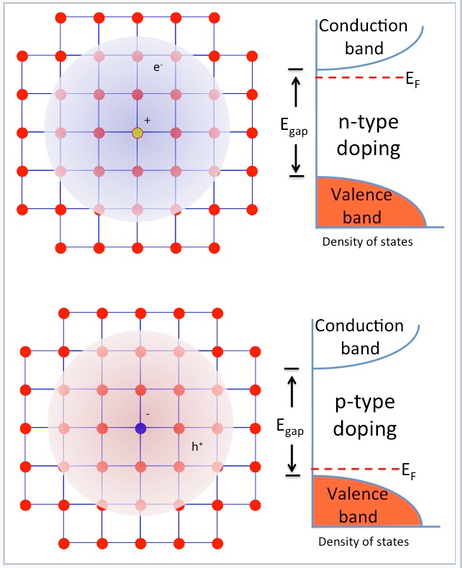
N- und p-Typ-Dotierung von Halbleitern beinhaltet die Substitution von Elektronendonatoratomen (hellorange) oder Akzeptoratomen (blau) im Gitter. Diese Substitutionen führen zusätzliche Elektronen bzw. Löcher ein, die durch thermische Energie leicht ionisiert und zu freien Ladungsträgern werden können. Das Fermi-Niveau eines dotierten Halbleiters liegt einige zehn mV unterhalb des Leitungsbandes (n-Typ) oder oberhalb des Valenzbandes (p-Typ).

Wie bereits erwähnt, verändert die Dotierung von Halbleitern ihre Leitfähigkeit drastisch. Zum Beispiel beträgt die intrinsische Ladungsträgerkonzentration in Si bei 300 K etwa 1010 cm-3. Das Massenwirkungsgleichgewicht für Elektronen und Löcher gilt auch für dotierte Halbleiter, so dass wir schreiben können:

\

Wenn wir P für Si auf dem Niveau von einem Teil pro Million ersetzen, beträgt die Elektronenkonzentration etwa 1016 cm-3, da sich etwa 1022 Si-Atome/cm3 im Kristall befinden. Nach der Massenwirkungsgleichung gilt für n = 1016, dass p = 104 cm-3. Aus dieser Berechnung ergeben sich drei Konsequenzen:

• Die Dichte der Ladungsträger im dotierten Halbleiter (1016 cm-3) ist viel höher als im undotierten Material (~1010 cm-3), so dass auch die Leitfähigkeit um viele Größenordnungen höher ist.
• Die Aktivierungsenergie für die Leitung beträgt nur 40-50 meV, so dass sich die Leitfähigkeit mit der Temperatur kaum ändert (im Gegensatz zum intrinsischen Halbleiter)
• Die Minoritätsträger (in diesem Fall Löcher) tragen nicht zur Leitfähigkeit bei, weil ihre Konzentration so viel niedriger ist als die des Majoritätsträgers (Elektronen).

Auch bei p-Typ-Materialien wird die Leitfähigkeit von Löchern dominiert und ist ebenfalls viel höher als die des intrinsischen Halbleiters.

Chemie der Halbleiterdotierung. Manchmal ist es nicht sofort ersichtlich, welche Art von Dotierung (n- oder p-Typ) durch das „Durcheinanderbringen“ eines Halbleiterkristallgitters hervorgerufen wird. Neben der Substitution von Fremdatomen auf normalen Gitterplätzen (die oben genannten Beispiele für Si) ist es auch möglich, mit Leerstellen – fehlenden Atomen – und mit Zwischengitteratomen – zusätzlichen Atomen auf normalerweise nicht besetzten Plätzen – zu dotieren. Einige einfache Regeln lauten wie folgt:

• Bei Substitutionen führt das Hinzufügen eines Atoms auf der rechten Seite des Periodensystems zu einer Dotierung vom n-Typ und das Hinzufügen eines Atoms auf der linken Seite zu einer Dotierung vom p-Typ.

Wird TiO2 beispielsweise mit Nb auf einigen der Ti-Stellen oder mit F auf O-Stellen dotiert, so ist das Ergebnis eine Dotierung vom n-Typ. In beiden Fällen hat das Fremdatom ein Valenzelektron mehr als das Atom, das es ersetzt hat. In ähnlicher Weise führt das Ersetzen von Ga in GaAs durch eine kleine Menge Zn oder von Ni in NiO durch eine kleine Menge Li zu einer Dotierung vom p-Typ.

• Leerstellen in Anionen führen zu einer Dotierung vom n-Typ, und Leerstellen in Kationen zu einer Dotierung vom p-Typ.

Beispiele sind Anionenleerstellen in CdS1-x und WO3-x, die beide n-Typ-Halbleiter ergeben, und Kupferleerstellen in Cu1-xO, das einen p-Typ-Halbleiter ergibt.

• Zwischengitterkationen (z. B. Li) geben Elektronen an das Gitter ab, was zu einer n-Typ-Dotierung führt. Zwischengitteranionen sind eher selten, würden aber zu einer Dotierung vom p-Typ führen.

Gelegentlich können sowohl p- als auch n-Typ-Dotierstoffe im selben Kristall vorhanden sein, z. B. B- und P-Verunreinigungen in einem Si-Gitter oder Kationen- und Anionenlücken in einem Metalloxidgitter. In diesem Fall kompensieren sich die beiden Dotierungsarten gegenseitig, und die Art der Dotierung wird durch diejenige bestimmt, die in höherer Konzentration vorliegt. Ein Dotierstoff kann auch auf mehr als einer Stelle vorhanden sein. So kann Si beispielsweise sowohl die Ga- als auch die As-Stellen in GaAs besetzen, und die beiden Substitutionen gleichen sich gegenseitig aus. Si hat jedoch eine leichte Präferenz für die Ga-Stelle, was zu einer n-Typ-Dotierung führt.