Viime aikoina eräs kollegani kysyi minulta muutamia kysymyksiä, kuten ”miksi meillä on niin paljon aktivointifunktioita?”.”, ”miksi yksi toimii paremmin kuin toinen?”, ”mistä tiedämme, mitä kannattaa käyttää?”, ”onko se hardcore-matematiikkaa?” ja niin edelleen. Joten ajattelin, miksi en kirjoittaisi artikkelia siitä niille, jotka tuntevat neuroverkkoa vain perustasolla ja siksi ihmettelevät aktivointifunktioita ja niiden ”miksi-miten-miten-matematiikkaa!”.
Huomautus: Tämä artikkeli olettaa, että sinulla on perustiedot keinotekoisesta ”neuronista”. Suosittelen tutustumaan neuroverkkojen perusteisiin ennen tämän artikkelin lukemista paremman ymmärryksen saamiseksi.
Aktivaatiofunktiot
Mitä keinotekoinen neuroni siis tekee? Yksinkertaisesti sanottuna se laskee ”painotetun summan” syötteestään, lisää siihen harhaa ja päättää sitten, pitäisikö se ”laukaista” vai ei ( joo joo, aktivointifunktio tekee tämän, mutta mennäänpä hetkeksi virran mukana ).
Tarkastellaan siis neuronia.
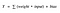
Nyt Y:n arvo voi olla mitä tahansa välillä -inf ja +inf. Neuroni ei todellakaan tiedä arvon rajoja. Miten siis päätämme, pitäisikö neuronin syttyä vai ei ( miksi tämä syttymismalli? Koska opimme sen biologiasta, että näin aivot toimivat ja aivot ovat toimivan todistuksen mahtavasta ja älykkäästä järjestelmästä ).
Päätimme lisätä ”aktivointifunktioita” tähän tarkoitukseen. Tarkistamaan neuronin tuottaman Y-arvon ja päättämään, pitäisikö ulkopuolisten yhteyksien pitää tätä neuronia ”laukaistuna” vai ei. Tai pikemminkin sanotaan – ”aktivoituna” vai ei.
Aktiivifunktio
Ensimmäisenä mieleemme tulee, miten olisi kynnysarvoon perustuva aktivointifunktio? Jos Y:n arvo on tietyn arvon yläpuolella, julistetaan se aktivoiduksi. Jos se on alle kynnysarvon, sanotaan ettei se ole. Hmm hienoa. Tämä voisi toimia!
Aktivaatiofunktio A = ”aktivoitu” jos Y > kynnysarvo muuten ei
Vaihtoehtoisesti A = 1 jos y> kynnysarvo, 0 muuten
Noh, se mitä juuri teimme, on ”askelfunktio”, katso alla oleva kuva.
Sen ulostulo on 1 ( aktivoituu), kun arvo > 0 (kynnysarvo) ja ulostulot ovat 0 ( ei aktivoitu) muutoin.
Hienoa. Tästä saadaan siis aktivointifunktio neuronille. Ei sekaannuksia. Tässä on kuitenkin tiettyjä haittoja. Jotta ymmärtäisit sen paremmin, mieti seuraavaa.
Esitellään, että olet luomassa binääriluokittelijaa. Jotain, jonka pitäisi sanoa ”kyllä” tai ”ei” ( aktivoi tai ei aktivoi ). Step-funktio voisi tehdä sen puolestasi! Juuri niin se tekee, sanoo 1 tai 0. Ajattele nyt käyttötapausta, jossa haluaisit kytkeä useita tällaisia neuroneja, jotta saataisiin lisää luokkia. Luokka1, luokka2, luokka3 jne. Mitä tapahtuu, jos useampi kuin 1 neuroni ”aktivoituu”. Kaikki neuronit antavat tulokseksi 1 (askelfunktiosta). Mitä sinä nyt päättäisit? Mikä luokka on kyseessä? Hmm vaikeaa, monimutkaista.
Haluaisit verkon aktivoivan vain 1 neuronin ja muiden pitäisi olla 0 ( vain silloin voisit sanoa, että se luokitteli oikein / tunnisti luokan ). Ah! Tätä on vaikeampi treenata ja konvergoitua näin. Olisi ollut parempi, jos aktivointi ei olisi ollut binäärinen, vaan se olisi sanonut ”50 % aktivoitu” tai ”20 % aktivoitu” ja niin edelleen. Ja sitten jos useampi kuin 1 neuroni aktivoituu, voitaisiin löytää, millä neuronilla on ”korkein aktivoituminen” ja niin edelleen ( parempi kuin max, softmax, mutta jätetään se toistaiseksi ).
Tällöinkin, jos useampi kuin 1 neuroni sanoo ”100% aktivoitunut”, ongelma säilyy edelleen. tiedän! Mutta…koska ulostulolle on olemassa väliaktivointiarvot, oppiminen voi olla tasaisempaa ja helpompaa ( vähemmän kiemurtelevaa ) ja mahdollisuudet siihen, että useampi kuin 1 neuroni on 100% aktivoitunut, ovat pienemmät verrattuna askelfunktioon harjoittelun aikana ( riippuu myös siitä, mitä olet harjoittelemassa ja datasta ).
Ok, joten haluamme siis jonkun antavan meille välivaiheessa olevat ( analogiset ) aktivaatioarvot sen sijaan, että sanomme ”aktivoitunut” tai ”ei” ( binäärinen ).
Ensimmäinen asia mikä tulee mieleemme olisi Lineaarinen funktio.
Lineaarinen funktio
A = cx
Suoraviivainen funktio, jossa aktivointi on verrannollinen syötteeseen ( joka on neuronin painotettu summa ).
Tällä tavalla se antaa vaihteluväliä aktivoinneille, joten se ei ole binäärinen aktivointi. Voimme varmasti liittää muutaman neuronin yhteen ja jos useampi kuin 1 palaa, voisimme ottaa max ( tai softmax) ja päättää sen perusteella. Sekin on siis ok. Mikä tässä sitten on ongelmana?
Jos olet perehtynyt gradientti-laskeutumiseen harjoittelua varten, huomaisit, että tälle funktiolle derivaatta on vakio.
A = cx, derivaatta x:n suhteen on c. Eli gradientilla ei ole mitään suhdetta X:ään. Se on vakio-gradientti ja laskeutuminen tapahtuu vakio-gradientilla. Jos ennusteessa on virhe, takaperin etenemisen tekemät muutokset ovat vakioita eivätkä riipu syötteen muutoksesta delta(x) !!!
Tämä ei ole niin hyvä! ( ei aina, mutta kärsivällisyyttä ). On myös toinenkin ongelma. Ajattele kytkettyjä kerroksia. Jokainen kerros aktivoidaan lineaarisella funktiolla. Tuo aktivointi puolestaan menee seuraavalle tasolle syötteenä ja toinen kerros laskee painotetun summan tuolle syötteelle ja se puolestaan laukeaa toisen lineaarisen aktivointifunktion perusteella.
Ei ole väliä kuinka monta kerrosta meillä on, jos kaikki ovat luonteeltaan lineaarisia, niin viimeisen kerroksen lopullinen aktivointifunktio ei ole mitään muuta kuin vain lineaarinen funktio ensimmäisen kerroksen syötteestä! Pysähdy hetkeksi miettimään asiaa.
Tämä tarkoittaa, että nämä kaksi kerrosta ( tai N kerrosta ) voidaan korvata yhdellä kerroksella. Ah! Menetimme juuri kyvyn pinota kerroksia tällä tavalla. Riippumatta siitä, miten pinomme, koko verkko vastaa edelleen yhtä kerrosta lineaarisella aktivaatiolla ( lineaaristen funktioiden yhdistelmä lineaarisella tavalla on edelleen toinen lineaarinen funktio ).
Mennäänkö eteenpäin?
Sigmoidifunktio
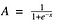
>
No, tämähän näyttää tasaiselta ja ”askelfunktion kaltaiselta”. Mitä hyötyä tästä on? Mieti asiaa hetki. Ensinnäkin se on luonteeltaan epälineaarinen. Myös tämän funktion yhdistelmät ovat epälineaarisia! Hienoa. Nyt voimme pinota kerroksia. Entä ei-binääriset aktivoinnit? Kyllä, sekin!. Se antaa analogisen aktivoinnin toisin kuin askelfunktio. Sillä on myös tasainen gradientti.
Ja jos huomaatte, X-arvojen -2 ja 2 välillä Y-arvot ovat hyvin jyrkkiä. Mikä tarkoittaa, että mikä tahansa pieni muutos X:n arvoissa tuolla alueella aiheuttaa Y:n arvojen muuttumisen merkittävästi. Ah, se tarkoittaa, että tällä funktiolla on taipumus viedä Y-arvot käyrän kumpaankin päähän.
Näyttää siltä, että se on hyvä luokittimeksi ottaen huomioon sen ominaisuuden? Kyllä ! Se todellakin on. Sillä on taipumus tuoda aktivoinnit käyrän kummallekin puolelle ( esimerkiksi x = 2 yläpuolelle ja x = -2 alapuolelle). Tekee selkeitä erotteluja ennusteessa.
Tämän aktivointifunktion toinen etu on, toisin kuin lineaarisen funktion, aktivointifunktion ulostulo tulee aina olemaan alueella (0,1) verrattuna lineaarisen funktion (-inf, inf). Joten meillä on aktivointimme sidottu alueelle. Hienoa, se ei sitten räjäytä aktivaatioita.
Tämä on hienoa. Sigmoidifunktiot ovat yksi yleisimmin käytetyistä aktivaatiofunktioista nykyään. Mitä ongelmia tässä sitten on?
Jos huomaat, sigmoidifunktion kummassakin päässä Y-arvoilla on taipumus reagoida hyvin vähän muutoksiin X:ssä. Mitä se tarkoittaa? Gradientti tuolla alueella tulee olemaan pieni. Siitä syntyy ”katoavan gradientin” ongelma. Hmm. Mitä siis tapahtuu, kun aktivaatiot yltävät lähelle käyrän ”lähes vaakasuoraa” osaa kummallakin puolella?
Gradientti on pieni tai se on kadonnut ( ei voi tehdä merkittävää muutosta äärimmäisen pienen arvon takia ). Verkko kieltäytyy oppimasta lisää tai on rajusti hidas ( riippuen käyttötapauksesta ja kunnes gradientti/laskenta osuu liukulukuarvojen rajoihin ). On olemassa tapoja kiertää tämä ongelma ja sigmoidi on edelleen hyvin suosittu luokitusongelmissa.
Tanh-funktio
Toinen aktivointifunktio, jota käytetään on tanh-funktio.
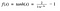
Hm. Tämä näyttää hyvin samanlaiselta kuin sigmoidi. Itse asiassa se on skaalattu sigmoidifunktio!

Ok, nyt tällä on ominaisuuksiltaan samankaltaisia piirteitä kuin sigmoidilla, josta keskustelimme edellä. Se on luonteeltaan epälineaarinen, joten hienoa, että voimme pinota kerroksia! Se on sidottu alueeseen (-1, 1), joten aktivointien räjähtämisestä ei ole huolta. Mainittakoon, että gradientti on voimakkaampi tanh:lle kuin sigmoidille ( johdannaiset ovat jyrkempiä). Päätös sigmoidin tai tanh:n välillä riippuu gradientin voimakkuutta koskevista vaatimuksistasi. Kuten sigmoidilla, myös tanh:lla on häviävän gradientin ongelma.
Tanh on myös hyvin suosittu ja laajalti käytetty aktivointifunktio.
ReLu
Myöhemmin tulee ReLu-funktio,
A(x) = max(0,x)
ReLu-funktio on yllä olevan kuvan mukainen. Se antaa tulosteen x, jos x on positiivinen ja muuten 0.
Ensi silmäyksellä tässä näyttäisi olevan samoja ongelmia kuin lineaarisessa funktiossa, koska se on lineaarinen positiivisella akselilla. Ensinnäkin ReLu on luonteeltaan epälineaarinen. Ja ReLun yhdistelmät ovat myös epälineaarisia! ( itse asiassa se on hyvä approksimaattori. Mikä tahansa funktio voidaan approksimoida ReLun yhdistelmillä). Hienoa, tämä siis tarkoittaa, että voimme pinota kerroksia. Se ei kuitenkaan ole sidottu. ReLu:n alue on [0, inf). Tämä tarkoittaa, että se voi räjäyttää aktivaation.
Toinen seikka, josta haluaisin keskustella tässä, on aktivaation harvuus. Kuvitellaan iso neuroverkko, jossa on paljon neuroneja. Sigmoidin tai tanh:n käyttäminen aiheuttaa sen, että lähes kaikki neuronit palavat analogisesti ( muistatko? ). Tämä tarkoittaa, että lähes kaikki aktivaatiot käsitellään kuvaamaan verkon ulostuloa. Toisin sanoen aktivaatio on tiheä. Tämä on kallista. Ihannetapauksessa haluaisimme, että muutama neuroni verkostossa ei aktivoidu ja siten teemme aktivoinneista harvoja ja tehokkaita.
ReLu antaa meille tämän edun. Kuvitellaan verkko, jossa on satunnaisesti alustetut painot ( tai normalisoidut ) ja lähes 50 % verkosta tuottaa 0 aktivaatiota ReLu:n ominaisuuden vuoksi ( ulostulo 0 negatiivisille x:n arvoille ). Tämä tarkoittaa, että vähemmän neuroneja laukeaa ( harva aktivaatio ) ja verkko on kevyempi. Woah, hienoa! ReLu näyttää olevan mahtava! Kyllä se on, mutta mikään ei ole virheetöntä… Ei edes ReLu.
Koska ReLussa on vaakasuora viiva ( negatiivisen X:n kohdalla ), gradientti voi mennä kohti 0:a. Aktivoinneille, jotka ovat ReLun tuolla alueella, gradientti on 0, minkä takia painoja ei säädetä laskeutumisen aikana. Se tarkoittaa, että ne neuronit, jotka menevät tuohon tilaan, lakkaavat reagoimasta virheen/syötteen vaihteluihin ( yksinkertaisesti koska gradientti on 0, mikään ei muutu ). Tätä kutsutaan kuolevaksi ReLu-ongelmaksi. Tämä ongelma voi aiheuttaa sen, että useat neuronit vain kuolevat eivätkä reagoi, jolloin merkittävä osa verkosta on passiivinen. ReLussa on muunnelmia tämän ongelman lieventämiseksi yksinkertaisesti tekemällä vaakasuorasta viivasta ei-vaakasuora komponentti . esimerkiksi y = 0.01x for x<0 tekee siitä hieman kaltevan viivan vaakasuoran viivan sijasta. Tämä on vuotava ReLu. Muitakin variaatioita on olemassa. Pääidea on antaa gradientin olla nollasta poikkeava ja palautua lopulta harjoittelun aikana.
ReLu on laskennallisesti vähemmän kallis kuin tanh ja sigmoidi, koska se sisältää yksinkertaisempia matemaattisia operaatioita. Tämä on hyvä huomioida, kun suunnittelemme syviä neuroverkkoja.
Okei, kumpaa nyt käytämme?
Mitä aktivaatiofunktioita nyt käytämme. Tarkoittaako tämä, että käytämme vain ReLua kaikkeen mitä teemme? Vai sigmoidia vai tanhia? No, kyllä ja ei. Kun tiedät, että funktiolla, jota yrität approksimoida, on tietyt ominaisuudet, voit valita aktivointifunktion, joka approksimoi funktion nopeammin, mikä johtaa nopeampaan koulutusprosessiin. Esimerkiksi sigmoidi toimii hyvin luokittimessa ( katso sigmoidin kuvaaja, eikö se näytä ihanteellisen luokittimen ominaisuuksia? ), koska luokittimen funktion approksimointi sigmoidin yhdistelminä on helpompaa kuin esimerkiksi ReLu. Mikä johtaa nopeampaan koulutusprosessiin ja konvergenssiin. Voit käyttää myös omia mukautettuja funktioita!. Jos et tiedä, millaista funktiota yrität oppia, suosittelen ehkä aloittamaan ReLu:lla ja työskentelemään sitten taaksepäin. ReLu toimii useimmiten yleisenä approksimaattorina!
Tässä artikkelissa yritin kuvata muutamia yleisesti käytettyjä aktivointifunktioita. On olemassa muitakin aktivointifunktioita, mutta yleinen idea pysyy samana. Parempien aktivointifunktioiden tutkimus on edelleen käynnissä. Toivottavasti ymmärsit aktivointifunktion idean, miksi niitä käytetään ja miten päätämme, mitä niistä käytetään.