Aivan kuten kakkua voi olla kaksi pientä palaa tai yksi kaksi kertaa isompi pala, ja se on sama määrä. Siksi monet murtoluvut ovat ekvivalentteja, kuten 2/5 ja 4/10.


Mikä tahansa luku voidaan kirjoittaa murtolukuna
Kirjoita mikä tahansa kokonaisluku, joka on suurempi kuin 1, murtoluvuksi, koska minkä tahansa jakamattoman kokonaisluvun osien kokonaismäärä on yksi.
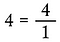
Murtolukujen kertominen suoraan ristiin
Murtolukujen kertominen on helppoa, kerro vain suoraan ristiin.
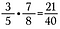
Huomautus: Sekaluvut on ensin muutettava epäsäännöllisiksi murtoluvuiksi, lue tästä lisää.
Kerroin millä tahansa ykkösen muodolla milloin tahansa
Lukua 1 kutsutaan multiplikatiiviseksi identiteetiksi, koska voimme kertoa sen millä tahansa luvulla ja luku pysyy samana. Tämä on tärkeää murtoluvuille, koska usein meidän on muutettava murtoluvun ulkonäköä muuttamatta sen arvoa.
Voin esimerkiksi muuttaa 1/3:n vastaavaksi murtoluvuksi 3/9 kertomalla sen luvulla 3/3.
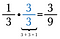
Yhtäsuurten osien yhteen- ja vähennyslasku
Murtolukuja yhteen- ja vähennyslaskujen yhteydessä murtoluvuilla nimittäjien on oltava samat. Siinä on järkeä. Jos haluamme yhdistää tai ottaa pois osia, meidän on puhuttava samankokoisista osista, muuten se menisi sekavaksi.
Mitä siis tehdään, jos murtoluvut eivät ole samankokoisia?
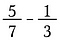
Kerroin muotoon yksi, jotta muuttuisi nimittäjät samankokoisiksi. Pohjimmiltaan jaamme murtoluvut pienempikokoisiksi paloiksi, kunnes ne ovat samankokoisia. Tätä kutsutaan yhteisen nimittäjän löytämiseksi.
Tosiasiassa mikä tahansa yhteinen nimittäjä kelpaa, mutta ihmiset etsivät mieluummin pienimmän. Tässä tapauksessa pienin luku, johon sekä 7 että 3 menevät ilman jäännöstä, on 21. Kerro siis ensimmäinen murtoluku 3/3:lla ja toinen 7/7:llä.
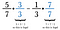
Jos et keksi pienintä yhteistä nimittäjää, voit aina laskea kumpikin murtoluku päinvastaisella nimittäjäarvolla. Joskus, kuten tässä tapauksessa, se osoittautuu pienimmäksi yhteiseksi nimittäjäksi. Jos se ei ole, vähennä vastauksesi lopussa.
Kun nimittäjät täsmäävät, vähennä osoittajat, niin saat 8/21.
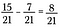
Tämä onnistuu niin kuin odottaa saattaa. Kuvallisesti aloitetaan 15 palasta 21 yhteensä.

Poistetaan 7:stä 15:stä sinisestä palikasta väritys.

Jolloin jäljelle jää odotetusti 8/21.
Vaihda ensin sekaluvut
Sekaluku on kokonaisluvun ja murtoluvun yhdistelmä.
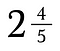
Sekaluvut eivät pelaa hyvin muiden murtolukujen kanssa. Ne kannattaa ensin muuntaa epäsäännöllisiksi murtoluvuiksi.
Huomautus: Epäsäännöllinen murtoluku on murtoluku, jonka osoittaja on suurempi kuin nimittäjä, joten sen arvo on suurempi kuin yksi.
Sekaluvun muuntaminen on oikeastaan yhteenlaskua
Muuntaaksesi 2 ja 4/5 epäsäännöllisiksi murtoluvuiksi laske yhteenlaskutoimitukset: 2 + 4/5.
Vaihe 1: Aloita muuttamalla 2 uudelleen 2:ksi/1.
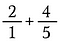
Vaihe 2: Kerro 2/1:llä 5/5:llä, jotta saat ekvivalentin murtoluvun 10/5, jonka haluttu yhteinen nimittäjä on 5.
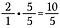
Vaihe 3: Lasketaan yhteen 10/5 + 4/5.
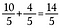
Tuloksemme on ekvivalentti epäsäännöllinen murtoluku 14/5.
Muuntaaksemme takaisin sekaluvuksi suoritamme jaon. Esimerkiksi 5 menee kahdesti 14:ään (koska 5 x 2 = 10) ja jäljelle jää 4 kappaletta.
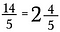
Vertailemalla murtolukuja ristitulon avulla
Esitettäköön, että haluaisimme määritellä kumpaa murtolukua on enemmän: 5/12 vai 6/13.
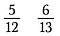
Vaihe yksi: Kerro lävistäjä ja kirjoita tuote osoittajan yläpuolelle.
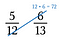
Vaihe kaksi: Kerro toinen diagonaali ja kirjoita sen tulo sen osoittajan yläpuolelle.
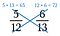
Vaihe kolme: Vertaile tuotteita. Se puoli, jolla on suurempi tuote, on suurempi murtoluku. Tässä tapauksessa siis 5/12 on pienempi kuin 6/13.
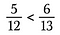
Voidaan myös ristikkäistuotosten avulla määrittää, ovatko murtoluvut yhtä suuria.
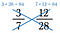
Lukujen 3/7 ja 12/28 ristituotto on molempien arvot 84, joten 3/7 = 12/28.
Korjaa mitä tahansa, joka jakaa yhteen
Murtolukujen paras puoli on se, että voit löytää paljon mahdollisuuksia korjattavaksi. Mikä tekee niistä nopeita ja helppoja hallita.
Esitettäköön, että minulla on murtoluku 8/10. Sekä 8 että 10 voidaan kirjoittaa uudelleen siten, että tekijä on 2.
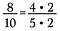
Koska 2/2 = 1, voin perua kakkoset, jolloin jäljelle jää pelkistetty murtoluku 4/5.
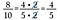
Hyödynnän tätä strategiaa helpottaakseni myös murtolukujen kertomista.
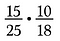
Aloita kirjoittamalla jokainen luku uudelleen tekijöihin.
>
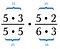
Laskekaa pois kaikki luvun 1:llä jakavat numeroparit. Esimerkiksi 5/5 = 1.
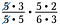
Minulla on toinenkin 5:n pari sekä 3:n pari, jotka myös jakautuvat 1:een.
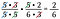
Oops! Olisin voinut kirjoittaa 6 uudelleen 2 x 3:ksi ja perua kakkosparin. Ei haittaa, jos joku tekijä jää huomaamatta, jatka vain, kunnes saat ne kaikki.
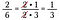
Jos olisin suoraan kertonut 15/25 kertaa 10/18 se olisi ollut paljon aritmeettista laskentaa, peruuttamista käyttämällä vähennän murtoluvut valmiiksi ja teen kertomisesta yksinkertaisempaa.
Kertolaskun käyttäminen murtolukujen jakamiseen
Murtolukujen jakamisen käsite on helppo yksinkertaisilla esimerkeillä, kuten:

Kokonaisuudessa on kaksi puolikasta, joten viidessä kokonaisuudessa on 10 puolikasta.
Mutta käsite muuttuu hankalaksi monimutkaisempien murtolukujen kanssa.
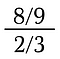
Tehtävän ratkaisemiseksi hyödynnämme kahta tosiasiaa:
- Voitamme kertoa millä tahansa ykkösen muodolla (esim.eli mitä tahansa itsensä yli)
- Kertomalla 3/2:n käänteisluvulla, joka on 2/3, saadaan peruuttamisen kautta 1
Vaihe yksi: Aloitetaan kertomalla käänteisluvulla itsensä yli.
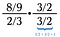
Nyt meillä on kaksi pienempää ongelmaa ratkaistavana (sininen ja vihreä).
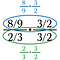 >
>
>Vaihe kaksi: Peruuta kaikki, mikä jakaa 1:llä alemmassa (vihreässä) murtoluvussa. Tämän pitäisi aina johtaa tulokseen 1.

Nyt jäljelle jää ylempi ongelma ratkaistavaksi.
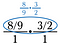
Kolmas askel: Käytä peruuttamista murtoluvun esipienennykseen. Kun olet tehnyt nämä vähennykset, kerro poikki saadaksesi 4/3.

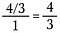
Lyhennysliitäntä
Tämä on pitkän käden mekaniikka, joka tarkoittaa ”käännä ja kerro”.”
Voidaan jättää kertominen käänteisluvulla alhaalla väliin, koska se kumoutuu aina 1:ksi. Siksi tarvitsee vain kertoa osoittaja nimittäjän käänteisluvulla.

Plussaa: teoriaa, siltä varalta, että se kiinnostaa…
Hyvä kysymys! Yleistäen, tee kaksi murtolukua käyttäen kirjaimia a, b, c ja d kuvaamaan neljää eri lukua.
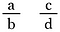
Kummatkin murtoluvut kerrotaan b-d:llä (näin saadaan nimittäjät mitätöityä).
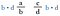
Nyt perutaan vasemmanpuoleiset b:t ja oikeanpuoleiset d:t, koska ne jakautuvat 1:een. Meillä ei ole enää murtolukuja, vaan vain tuotteet d-a ja c-b.
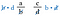
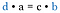
Palataan takaisin alkuperäisiin murtolukuihin. Nämä ovat samat tuotteet kuin jos olisimme kertoneet diagonaalit. Siksi oikotie on verrata ristituloa.
❤ Pysy yhteydessä ❤
Ole ajan tasalla kaikesta, mitä Math Hacks tekee!