Miten auttaa oppilaita, jotka kamppailevat sanaongelmien kanssa

”He osaavat matematiikan. He eivät vain osaa tehdä sanallisia ongelmia. Se on heidän lukutaitonsa ongelma.”

Ms Hartwell selitti, miksi hänen oppilaansa olivat kamppailleet osavaltion kokeissa. Hän tunsi oppilaansa ja oli tehnyt runsaasti arviointeja. Hän oli varma, että heidän vaikeuksissaan oli kyse lukutaidosta.

”En ymmärrä, miksi he tekevät lukemisesta niin vaikeaa. Lapset tekevät jo kielitaidon kokeen.”

Olin saanut Hartwellin (ja muiden hänen koulunsa oppilaiden) kanssa yhteyden New Yorkin kaupungin ohjelmaan, jolla pyrittiin parantamaan matemaattisia saavutuksia. Tavoitteena oli tuoda käsitteellinen matematiikka ”Tier 1” -kouluihin. Tier 1 -koulut olivat kouluja, jotka olivat kaupungin kärjessä kolmella alueella. Alhaisin tulotaso, alhaisimmat koetulokset ja korkein värillisten oppilaiden osuus.

Olin kuullut ”lukutaidon” selityksen muilta ohjelmaan osallistuneilta opettajilta. Ja siinä oli järkeä. Jos oppilaat osasivat matematiikkaa, miksi muuten he kamppailivat kokeessa, jossa oli paljon sanatehtäviä?

Mutta siinä oli juju. Kolmen viime vuoden aikana luku- ja kirjoitustaidon taso oli noussut 30-40 prosentista koko kaupungissa. Samaan aikaan matematiikan tulokset olivat pysyneet lähes ennallaan.

Jos kyse olisi lukemisen ongelmasta, lukupisteiden nousun pitäisi vapauttaa räjähdysmäinen kasvu matematiikassa. Sitä paitsi sanatehtävien kieli ei vaikuttanut tarpeeksi monimutkaiselta aiheuttaakseen ongelmia.

Seuraavalla tunnilla minun oli määrä käydä neiti Hartwellin luokassa. Hän oli suunnitellut oppitunnin sanaongelmista, joten voisin nähdä ongelman omakohtaisesti.

Over-Scaffolding Word Problems

Opiskelijat istuivat pyöreissä pöydissä, ja hän seisoi edessä. Hänellä ja hänen oppilaillaan oli kaikilla kädessä pidettävät valkotaulut.

He avasivat oppikirjansa sivulle 47, ja hän luki ääneen sanaongelman. ”Sarahilla on 40 kiloa porkkanoita hevosilleen. Jos hänellä on 100 hevosta, kuinka monta kiloa kukin hevonen saa?”

”OK luokka, hänellä on 40 kiloa, jotka hän antaa jokaiselle hevoselle. Mitä operaatiota me siis tarvitsemme?”

Hän osoitti ankkuritaulukkoa, jossa oli lueteltu kunkin operaation ”avainsanat”. ’Kukin’ oli jakoluettelon kärjessä.

”Jako!” luokka vastasi.

”Aivan. Miten siis jaamme pienen luvun isolla luvulla?”

Luokka oli hiljaa. Ms Hartwell piirsi taululleen vinculumin (pitkän jaon talon). Oppilaat kopioivat, kun hän laittoi 40 talon alle ja 100 sen ulkopuolelle.

”Nyt 100 ei mahdu 40:een, joten meidän on lisättävä desimaali.” Hän muutti 40:n luvuksi 40,0. ”Kuinka monta kertaa 100 mahtuu 400:aan?”

Muutama oppilas huusi ”Neljä!”.

”Juuri niin. Nyt meidän täytyy laittaa desimaaliluku myös osamääräämme. Lopullinen vastauksemme on?”

Luokka luki taululta vastauksen ”0,4”.

Hän antoi samanlaisen tehtävän ja osoitti seinällä olevaa ”CUBES”-julistetta. ”Muistakaa ympyröidä numerot ja laatikoida avainsanat.”

Hän kiersi ympäriinsä, kun oppilaat työskentelivät. Jotkut kysyivät, mihin desimaaliluku laitetaan. Toisilla oli vaikeuksia rivittää pitkän jakolaskun vähennysosaa. Jotkut oppilaat työskentelivät pareittain, ja toinen teki laskutoimitukset, kun toinen kopioi.

Tunnin loppuun mennessä kaikilla oli oikea vastaus paperillaan. ”Näetkö?” Neiti Hartwell huomautti, ”he kaikki osaavat matematiikan.”

Mitä meni pieleen?

Mikäli tämä on äärimmäinen esimerkki, monet neiti Hartwellin tekemistä virheistä ovat itse asiassa melko yleisiä.

Yliopetusta tapahtuu, kun annamme oppilaille liikaa tukea. Vaikka on tavallista, että opettajat ovat ylpeitä siitä, että he antavat oppilaille ”niin paljon tukea kuin he tarvitsevat”, liiallinen tukeminen on eri asia.

Termi ”scaffolding” on peräisin Lev Vygotskyn työstä. Hän keksi termin ”Zone of Proximal Development”. ZPD:hen kuuluvat asiat, jotka ovat juuri oppijan ulottumattomissa. Hän ei pysty siihen yksin, mutta hän pystyy siihen tuen avulla. ”Telineillä” voimme siirtää nämä taidot oppijan ydintaitoihin.

Vygotskyn lähikehityksen vyöhyke

Mitä usein unohdetaan, on se, että telineitä sovelletaan vain taitoihin, jotka ovat jo oppijan lähikehityksen vyöhykkeellä. On olemassa koko joukko taitoja, jotka ovat tällä hetkellä oppijan ulottumattomissa. Kun yritämme tukea näitä taitoja, aiheutamme enemmän haittaa kuin hyötyä.

Yksi ongelma liiallisessa tukemisessa on se, että oppilaat eivät koskaan sisäistä tavoiteltuja taitoja. Kun autamme oppilasta jossakin hänen ZPD:nsä ulkopuolella olevassa asiassa, hän tarvitsee aina apuamme. Ainakin siihen asti, kunnes tunnistamme välitaidot, jotka ovat heidän ZPD:nsä.

Toinen ongelma on, että liiallinen ohjaaminen antaa meille vääränlaisen onnistumisen tunteen. Tässä tapauksessa neiti Hartwell uskoi, että hänen oppilaansa pystyivät ”tekemään matematiikan” sanatehtävässä. Todellisuudessa he vain jäljittelivät hänen toimintaansa. Ei ollut mitään syytä uskoa, että he pystyisivät itse löytämään samanlaisen ratkaisun.

Hän myös poisti koko ”muotoiluprosessin” ongelmanratkaisuprosessista. Monet opettajat pitävät ymmärtämistä ja muotoilua samana asiana, mutta muotoilu on erillinen matemaattinen osaaminen.

Ja se saattaa olla juuri se puuttuva ainesosa tavasta, jolla tällä hetkellä opetat sanaongelmia.

Luokkahuoneresurssit ja ammatillinen oppiminen

Formulation: Avain menestykseen sanaongelmissa

Sanaongelmien muotoileminen edellyttää niiden ymmärtämistä. Mutta se menee sitä pidemmälle. Muotoilu on enemmänkin kääntämistä kuin ymmärtämistä.

Kun oppilas lukee sanaongelman, hänen on ensin muutettava kirjaimet äänteiksi (dekoodaus). Sitten hänen on ymmärrettävä, mitä sanat tarkoittavat (sanasto). Heidän on ymmärrettävä, miten sanat sopivat yhteen lauseessa (syntaksi). Lopuksi ymmärtäminen syntyy, kun nämä osat yhdistetään merkityksen muodostamiseksi.

Useimmat kuudennen luokan oppilaat voisivat lukea neiti Hartwellin ongelman ja ymmärtää helposti, että Sarah jakaa porkkanoita hevosilleen. Mutta paljon harvempi yhdistää porkkanoiden ”jakamisen” jakamiseen.

Tämä on kohta, joka kompastuttaa monia opettajia. Se tuntuu meistä niin itsestään selvältä. ”Hän kirjaimellisesti jakaa porkkanat. Miten he eivät voi nähdä, että se on jakamista.”

Eivät he vain näe. Jos he näkisivät, et näkisi avainsanataulukoita roikkumassa matematiikan luokkahuoneissa. Ja kaikki juontaa juurensa siihen, kun opettelemme ensimmäistä kertaa operaatioita.

Miksi oppilaat kamppailevat muotoilun kanssa

Monissa kouluissa monet opettajat opettavat oppilaille, että matematiikka on järjenkäyttöä. Toisissa taas matematiikkaa opetetaan muistamisen oppiaineena.

Esimerkki ”matematiikasta muistamisena” on, kun oppilaat painavat matematiikan faktat ulkoa. Mutta myös algoritmit ovat muistamista. Laita 120 47:n päälle. Noudata näitä ohjeita yhteenlaskuun, näitä vähennyslaskuun ja näitä kertolaskuun.

Opiskelijat voivat toistaa näitä vaiheita ymmärtämättä lukujen kokoa tai edes sitä, mitä operaatiot tarkoittavat.

Kun aloitamme käsitteistä (käyttämällä visuaalisia malleja tai numerolauseet), oppilaat oppivat, mitä operaatiot tarkoittavat. Kun siirrymme suoraan algoritmiin, oppilaat ajattelevat operaatioita satunnaisten vaiheiden sarjana.

Vuosi toisensa jälkeen oppilaat joutuvat muistamaan ja toistamaan. He suorittavat saman algoritmin 30 kertaa kotitehtäväksi. Vaihda numeroita, ja prosessi pysyy samana. Mutta antakaa heille sanatehtävä, ja nyt heidän on saatava siitä tolkkua.

Mitä testit kertovat meille päättelykyvystä

Voisimme antaa oppilaillemme 10 ongelmaa otsikolla ”Jaon sanatehtäviä”, jotta asia olisi helpompi. Heidän ei tarvitse edes lukea ongelmia. Heidän tarvitsee vain keksiä (tai arvailla), mikä luku on jakaja ja mikä jakolasku.

Mutta kun oppilaat osallistuvat valtion kokeeseen, tavoitteena ei ole helpottaa sitä. Tavoitteena on arvioida, mitä he osaavat tehdä omin voimin.

Kokeiden laatijat eivät halua kertoa heille, mitä operaatiota käyttää. He laittavat jopa jakamisen ja yhteenlaskun avainsanat samaan ongelmaan. ”Luokassa on 20 oppilasta. Jos jokaisella lapsella on kolme dollaria, kuinka paljon heillä on yhteensä?”

Kun oppilaat kamppailevat sanaongelmien kanssa, kyse ei ole vain sanaongelmista. Se tarkoittaa yleensä sitä, että he tekevät matematiikkaa ulkoa. Meidän on opetettava heille, että matematiikassa on kyse järjen hahmottamisesta.

Opiskelijat tarvitsevat strategioita ja prosesseja ratkaistakseen sanaongelmia

CUBESin kaltaisen järjestelmän ongelmana on osittain se, että se kutsuu itseään strategiaksi, mutta todellisuudessa se on prosessi.

Prosessi on sarja vaiheita. Kun tunnistat tehokkaan prosessin, voit toistaa sitä uudestaan ja uudestaan miettimättä liikaa. Algoritmit ovat prosessi. Samoin kuin jonottaminen ’pisimmästä lyhyimpään’ lounaskävelyä varten.

Strategia on eri asia. Strategiat vaativat syvällistä ymmärrystä. Ja kykyä soveltaa ymmärrystä uusissa tilanteissa.

Me emme voi valmistaa oppilaita jokaiseen skenaarioon, jonka he kohtaavat sanatehtävässä. Jotkut vaativat, että he yhdistävät erilaisia matemaattisia taitoja, joita he eivät ole koskaan aiemmin yhdistäneet. Tai ne saattavat vaatia oppilaita muuttamaan vaiheiden järjestystä oikean ratkaisun löytämiseksi.

Harkitse seuraavaa:

Sinulla on viisi litraa mehua koulun tapahtumaa varten, jossa on 100 oppilasta. Jos jokaiseen kuppiin mahtuu 3 oz, kuinka monta kuppia jokainen oppilas voi juoda? Kuinka paljon jää yli.

Ongelmanratkaisuprosessi voi auttaa oppilaita aloittamaan tämän ongelman ratkaisemisen. ”Tunnista, mitä kysytään”. ”Pohdi, mitä tietoa annetaan.”

Mutta ei ole olemassa mitään valmista prosessia, jonka voisimme opettaa heille ongelman varsinaista ratkaisemista varten. Siinä kohtaa strategia astuu kuvaan. Heidän on muunnettava yksiköt. Tunnustettava, että jaamme jäännösten kanssa, emmekä jaa kokonaan. Heidän pitäisi luultavasti myös järjestää operaatiot uudelleen jakamalla mehu kuppeihin ennen jakamista oppilaiden lukumäärällä.

Ei ole mitään ”temppua”, jolla oppilaat pääsisivät tähän. Heidän on ymmärrettävä operaatioiden merkitys. Heidän on ymmärrettävä matematiikka mielekkäänä oppiaineena. Ja heidän on toistuvasti harjoiteltava strategisen ajattelun soveltamista sanaongelmiin.

Pólyan prosessi sanaongelmien ratkaisemiseen

George Pólya oli vaikutusvaltainen unkarilainen matemaatikko ja Stanfordin professori, joka löysi prosessin, jota voitiin käyttää minkä tahansa ongelman ratkaisemiseen. Hänen työnsä on koskettanut lukemattomia matemaatikkoja ja opettajia, joista useimmat eivät tiedä hänen nimeään.

Itse asiassa CUBES ja muut niin sanotut ongelmanratkaisustrategiat perustuvat löyhästi hänen työhönsä. Ongelmana on, että ne yrittävät yksinkertaistaa sitä. Samalla ne poistavat kaiken, mikä muistuttaa syvällistä ajattelua.

Polya uskoi, että jokainen ongelma voidaan ratkaista neljässä vaiheessa: Ymmärrä, suunnittele, ratkaise ja pohdi. Mielestäni Polyan alkuperäinen nelivaiheinen prosessi sopii hyvin käytettäväksi kouluissa.

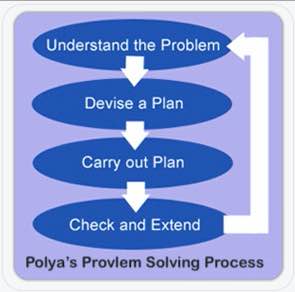Ymmärtääksemme ongelman tunnistamme, mitä tietoa on annettu ja mitä haluamme löytää. Tästä tulevat kuutioiden ’C’ ja ’U’. Jos oppilaat haluavat ympyröidä numerot ja alleviivata kysymyksen, hyvä. Minusta on parempi, että he kirjoittavat ne (yksikköineen) graafiseen järjestäjään, ainakin aluksi. Tämä auttaa heitä käsittelemään lukemaansa. Se auttaa myös minua opettajana arvioimaan heidän ymmärrystään, kun kävelen ympäri huonetta.

Seuraavaksi tulee hankala osuus. ’Suunnitelmassa’ muotoilemme ongelman. Otamme reaalimaailman skenaarion ja muutamme sen toiseksi matemaattiseksi esitykseksi.

Kolmas vaihe on ratkaiseminen. Jos olemme muotoilleet oikein, tässä vaiheessa laskemme. Oppilaat käyttävät yleensä algoritmia, mutta kannustan käyttämään myös yhtälöitä ja visuaalisia malleja.

Viimeiseksi oppilaat katsovat taaksepäin ja tarkistavat työnsä. Heidän tulisi myös pohtia prosessiaan. Jos tein virheen, miksi? Voisiko tämä strategia auttaa minua ratkaisemaan samankaltaisia ongelmia tulevaisuudessa?

Sanaongelmien ratkaisustrategiat

Sanaongelmien ratkaisemisprosessi on ehdottomasti hyödyllinen. Emme kuitenkaan voi teeskennellä, että mielekäs matematiikka opitaan vain vaiheita noudattamalla. Koko sanaongelmien tarkoitus on laajentaa matematiikkaa ”matemaattisia faktoja” ja algoritmeja pidemmälle.

On olemassa joitakin hyödyllisiä strategioita, jotka auttavat oppilaita muotoilussa. Aluksi opetan eksplisiittisesti useita eri strategioita.

Kun opetan strategioita, annan oppilaiden ratkaista ongelmia, jotka sopivat hyvin kyseiseen strategiaan. Jotkin ongelmatyypit sopivat todella hyvin ’Arvaa ja tarkista’ -strategian kanssa. Toiset sopivat paremmin ’Piirrä kuva’ -menetelmään.

Lopulta annan heille haastavia sanaongelmia, jotka voidaan ratkaista usealla eri tavalla. Kun heillä on työkalut vyöllään, he voivat valita, mikä on tilanteeseen parhaiten sopiva.

Strategioiden yhdistäminen voi myös olla erittäin tehokasta. Esimerkiksi kuvan piirtäminen voi usein auttaa muotoilussa. Jos viljelijällä on 18 riviä porkkanoita ja 10 porkkanaa jokaisella rivillä, oppilas voi aloittaa piirtämällä pellon. Jossain vaiheessa hän saattaa ajatella: ”Vau, tämä on kenttä”, ja tajuta, että hän voi kertoa käyttämällä mentaalimatematiikkaa, lauseketta tai algoritmia.

Toisissa tapauksissa oppilaat voivat käyttää visuaalisia malleja ongelman muotoilemiseen ja ratkaisemiseen.

Helpota oppilaitasi selviytymään haastavista sanaongelmista

Jos olet kuten monet opettajat, saatat olla huolissasi siitä, miten oppilaasi selviytyvät tästä kaikesta. Prosessit, strategiat, kriittinen ajattelu… siihen liittyy paljon.

Saatat jopa ajatella, että sanaongelmat tuntuivat helpommilta ennen tätä artikkelia. Jos näin on, pyydän anteeksi.

Vain tärkeintä on, ettet hukkua yrittämällä tehdä kaikkea kerralla. Aloita ratkaisemalla yksinkertainen sanaongelma Polyan prosessin avulla. Ota sitten joka viikko käyttöön uusi strategia. Vuoden loppuun mennessä tulet hämmästymään, miten pitkälle he ovat päässeet.

Mahdollisesti olet kiinnostunut syventymään luovaan ongelmanratkaisuun. Harkitse osallistumista käytännönläheiseen matematiikkatyöpajaan tai työskentelyä verkkovalmentajan kanssa.

Jos olet valmis tuomaan huomenna luokkahuoneeseesi Polyan, tämä graafinen järjestäjä on hyvä tapa aloittaa. Se tukee neliportaista prosessia ja auttaa sinua tunnistamaan, missä oppilaasi menevät harhaan.

Free Word Problem Organizer

Tietoa kirjoittajasta

Jeff Lisciandrello on Room to Discover -yrityksen perustaja ja oppilaskeskeiseen oppimiseen erikoistunut koulutuskonsultti. Hänen 3-Bridges Design for Learning -suunnitelmansa auttaa kouluja tutkimaan innovatiivisia käytäntöjä perinteisissä ympäristöissä. Hän auttaa mielellään opettajia omaksumaan tutkimukseen perustuvia ja yksilöllisiä lähestymistapoja opetukseen. Voit olla häneen yhteydessä Twitterissä @EdTechJeff

.