Kun aineisto on valmis analysoitavaksi, olisi aineiston tarkastelun perusteella arvioitava perusteellisesti, olisiko tilastollisia menetelmiä käytettävä puuttuvien tietojen käsittelyyn. Bell ym. pyrkivät arvioimaan puuttuvien tietojen laajuutta ja käsittelyä satunnaistetuissa kliinisissä tutkimuksissa, jotka julkaistiin heinäkuun ja joulukuun 2013 välisenä aikana BMJ-, JAMA-, Lancet- ja New England Journal of Medicine -lehdissä . Tunnistetuista 77:stä tutkimuksesta 95 prosenttia ilmoitti jonkin verran puuttuvia tulostietoja. Yleisimmin käytetty menetelmä puuttuvien tietojen käsittelyyn ensisijaisessa analyysissä oli täydellinen tapausanalyysi (45 %), yksittäinen imputaatio (27 %), mallipohjaiset menetelmät (esimerkiksi sekamallit tai yleistetyt estimointiyhtälöt) (19 %) ja moninkertainen imputaatio (8 %) .
Täydellinen tapausanalyysi
Täydellinen tapausanalyysi on tilastollinen analyysi, joka perustuu osallistujiin, joilla on täydelliset lopputulostiedot. Osallistujat, joilta puuttuu tietoja, jätetään analyysin ulkopuolelle. Kuten johdannossa kuvattiin, jos puuttuvat tiedot ovat MCAR, täydellisen tapausanalyysin tilastollinen teho pienenee pienemmän otoskoon vuoksi, mutta havaitut tiedot eivät ole vääristyneitä . Jos puuttuvat tiedot eivät ole MCAR-tietoja, täydellisen tapausanalyysin estimaatti intervention vaikutuksesta saattaa perustua, eli usein on olemassa riski hyötyjen yliarvioimisesta ja haittojen aliarvioimisesta . Katso kohta ”Pitäisikö puuttuvien tietojen käsittelyyn käyttää moninkertaista imputointia?”, jossa käsitellään yksityiskohtaisemmin mahdollista validiteettia, jos käytetään täydellistä tapausanalyysiä.
Yksittäinen imputointi
Käytettäessä yksittäistä imputointia puuttuvat arvot korvataan tietyllä säännöllä määritellyllä arvolla . On olemassa monia yksittäisen imputoinnin muotoja, esimerkiksi viimeinen havainto siirretään eteenpäin (osallistujan puuttuvat arvot korvataan osallistujan viimeisellä havaitulla arvolla), huonoin havainto siirretään eteenpäin (osallistujan puuttuvat arvot korvataan osallistujan huonoimmalla havaitulla arvolla) ja pelkkä keskiarvon imputointi . Yksinkertaisessa keskiarvon imputoinnissa puuttuvat arvot korvataan kyseisen muuttujan keskiarvolla . Yksinkertaisen imputoinnin käyttö johtaa usein vaihtelun aliarviointiin, koska jokaisella havaitsematta jääneellä arvolla on analyysissä sama painoarvo kuin tunnetuilla, havaituilla arvoilla . Yksittäisen imputoinnin pätevyys ei riipu siitä, ovatko tiedot MCAR; yksittäinen imputointi riippuu pikemminkin tietyistä oletuksista, joiden mukaan puuttuvat arvot ovat esimerkiksi identtisiä viimeisen havaitun arvon kanssa . Nämä oletukset ovat usein epärealistisia, ja siksi yksittäinen imputointi on usein potentiaalisesti vääristynyt menetelmä, ja sitä tulisi käyttää suurella varovaisuudella .
Moninkertainen imputointi
Moninkertainen imputointi on osoittautunut päteväksi yleiseksi menetelmäksi puuttuvien tietojen käsittelyyn satunnaistetuissa kliinisissä tutkimuksissa, ja tämä menetelmä on käytettävissä useimmille tietotyypeille . Seuraavissa kappaleissa kuvataan, milloin ja miten moninkertaista imputointia tulisi käyttää.
Pitäisikö moninkertaista imputointia käyttää puuttuvien tietojen käsittelyyn?
syitä, miksi moninkertaista imputointia ei tulisi käyttää puuttuvien tietojen käsittelyyn
Onko pätevää jättää puuttuvat tiedot huomioimatta?
Havainnoitujen tietojen analyysi (täydellinen tapauskohtainen analyysi), jossa puuttuvat tiedot jätetään huomioimatta, soveltuu kolmessa tilanteessa.
- a)
Täydellisen tapauksen analyysia voidaan käyttää ensisijaisena analyysinä, jos puuttuvien tietojen osuudet ovat alle noin 5 % (nyrkkisääntönä) ja on epätodennäköistä, että tietyt potilasryhmät (esimerkiksi erittäin sairaat tai erittäin ”terveet” osallistujat) nimenomaan häviävät seurannasta jossakin vertailtavista ryhmistä . Toisin sanoen, jos puuttuvien tietojen mahdollinen vaikutus on vähäinen, puuttuvat tiedot voidaan jättää huomiotta analyysissä. Epäselvissä tapauksissa voidaan käyttää best-worst- ja worst-best-case-herkkyysanalyysejä: ensin luodaan ”best-worst-case”-skenaariotietokokonaisuus, jossa oletetaan, että kaikilla seurantatulokset menettäneillä osallistujilla yhdessä ryhmässä (ryhmä 1) on ollut hyödyllinen lopputulos (esimerkiksi ei vakavia haittatapahtumia) ja että kaikilla niistä osallistujista, joilta puuttuvat tulokset puuttuvat, on ollut haitallista lopputulosta (esimerkiksi vakavia haittatapahtumia) . Tämän jälkeen luodaan ”pahimman mahdollisen” skenaarion mukainen tietokokonaisuus, jossa oletetaan, että kaikilla seurantaan menettäneillä osallistujilla ryhmässä 1 on ollut haitallinen lopputulos ja että kaikilla seurantaan menettäneillä osallistujilla ryhmässä 2 on ollut hyödyllinen lopputulos. Jos käytetään jatkuvia tuloksia, ”hyödyllinen tulos” voi olla ryhmän keskiarvo lisättynä kahdella keskihajonnalla (tai yhdellä keskihajonnalla) ryhmän keskiarvosta ja ”haitallinen tulos” voi olla ryhmän keskiarvo vähennettynä kahdella keskihajonnalla (tai yhdellä keskihajonnalla) ryhmän keskiarvosta . Dikotomisoitujen tietojen osalta nämä herkkyysanalyysit parhaasta ja huonoimmasta tapauksesta osoittavat puuttuvista tiedoista johtuvan epävarmuuden vaihteluvälin, ja jos tämä vaihteluväli ei anna laadullisesti ristiriitaisia tuloksia, puuttuvat tiedot voidaan jättää huomiotta. Jatkuvien tietojen osalta imputointi 2 SD:llä edustaa mahdollista epävarmuuden vaihteluväliä, kun otetaan huomioon 95 % havaituista tiedoista (jos ne ovat normaalisti jakautuneita).
- b)
Jos vain riippuvalla muuttujalla on puuttuvia arvoja ja apumuuttujia (muuttujia, joita ei ole sisällytetty regressioanalyysiin, mutta jotka ovat korreloituneina muuttujan kanssa, jolla on puuttuvia arvoja, ja/tai jotka ovat yhteydessä puuttuviin arvoihin) ei ole yksilöity, täydellistä tapauskohtaista analyysiä voidaan käyttää ensisijaisena analyysinä, ja silloin ei ole käytettävä mitään erityismenetelmiä puuttuvien tietojen käsittelemiseksi. Lisätietoa ei saada esimerkiksi käyttämällä moninkertaista imputointia, mutta keskivirheet voivat kasvaa moninkertaisen imputoinnin tuoman epävarmuuden vuoksi .
- c)
Kuten edellä mainittiin (ks. Menetelmät puuttuvien tietojen käsittelemiseksi), olisi myös perusteltua vain suorittaa täydellinen tapausanalyysi, jos on suhteellisen varmaa, että tiedot ovat MCAR (ks. Johdanto). On suhteellisen harvinaista, että on varmaa, että tiedot ovat MCAR. On mahdollista testata hypoteesi, että aineisto on MCAR, Littlen testillä , mutta voi olla epäviisasta rakentaa testien varaan, jotka osoittautuivat merkityksettömiksi. Jos siis on perusteltua epäillä, ovatko tiedot MCAR, vaikka Littlen testi olisi merkityksetön (ei onnistu hylkäämään nollahypoteesia siitä, että tiedot ovat MCAR), MCAR:ta ei pitäisi olettaa.
Onko puuttuvien tietojen osuus liian suuri?
Jos tietoja puuttuu suuria määriä, olisi harkittava, että ilmoitetaan vain täydellisen tapauskohtaisen analyysin tulokset ja keskustellaan sitten selkeästi tutkimustulosten tulkintarajoituksista. Jos puuttuvien tietojen käsittelyyn käytetään useita imputaatioita tai muita menetelmiä, se saattaa osoittaa, että tutkimuksen tulokset ovat vahvistavia, mitä ne eivät ole, jos puuttuvien tietojen määrä on huomattava. Jos puuttuvien tietojen osuus on hyvin suuri (esimerkiksi yli 40 %) tärkeiden muuttujien osalta, tutkimustuloksia voidaan pitää vain hypoteeseja tuottavina tuloksina. Harvinainen poikkeus on, jos puuttuvien tietojen taustalla olevaa mekanismia voidaan kuvata MCAR:ksi (ks. edellä oleva kappale).
Vaikuttavatko MCAR- ja MAR-oletukset molemmat epätodennäköisiltä?
Jos MAR-oletukset vaikuttavat epätodennäköisiltä puuttuvien tietojen ominaisuuksien perusteella, tutkimustulokset ovat vaarassa vääristyä ”epätäydellisten lopputulosdatatietojen vääristymisen” vuoksi, eikä mikään tilastollinen menetelmä voi varmuudella ottaa huomioon tätä potentiaalista vääristymistä . MNAR-tietojen käsittelyyn käytettävien menetelmien pätevyys edellyttää tiettyjä oletuksia, joita ei voida testata havaittujen tietojen perusteella. Parhaimman ja huonoimman tapauksen herkkyysanalyysit voivat osoittaa koko teoreettisen epävarmuusalueen, ja johtopäätökset olisi suhteutettava tähän epävarmuusalueeseen. Analyysien rajoituksista olisi keskusteltava perusteellisesti ja ne olisi otettava huomioon.
Onko lopputulosmuuttuja, jolla on puuttuvia arvoja, jatkuva ja onko analyyttinen malli monimutkainen (esim. vuorovaikutukset)?
Tässä tilanteessa voidaan harkita suoran maksimilikelihood-menetelmän käyttämistä, jotta vältetään mallin yhteensopivuusongelmat analyyttisen mallin ja moninkertaisen imputointimallin välillä, kun edellinen on yleisempi kuin jälkimmäinen. Yleisesti ottaen voidaan käyttää suoria maksimilikelihood-menetelmiä, mutta tietojemme mukaan kaupallisesti saatavilla olevia menetelmiä on tällä hetkellä saatavilla vain jatkuville muuttujille.
Milloin ja miten käyttää moninkertaista imputaatiota
Jos mikään edellä mainituista ”Syistä, miksi moninkertaista imputaatiota ei pitäisi käyttää puuttuvien tietojen käsittelyyn” ei täyty, voidaan käyttää moninkertaista imputaatiota. Kirjallisuudessa on viime vuosikymmeninä ehdotettu erilaisia menettelyjä puuttuvien tietojen käsittelemiseksi. Olemme hahmotelleet edellä mainittuja näkökohtia puuttuvien tietojen käsittelyyn käytettävistä tilastollisista menetelmistä kuviossa 1.
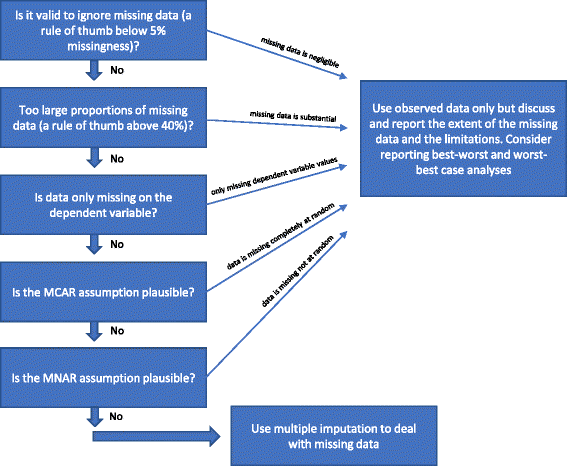
Virtauskaavio: milloin olisi käytettävä moninkertaista imputointia puuttuvien tietojen käsittelyyn analysoitaessa satunnaistettujen kliinisten tutkimusten tuloksia
Moninkertainen imputointi sai alkunsa 1970-luvun alussa, ja se on vuosien varrella saavuttanut kasvavaa suosiota . Moninkertainen imputointi on simulointiin perustuva tilastollinen tekniikka puuttuvien tietojen käsittelyyn . Moninkertainen imputointi koostuu kolmesta vaiheesta:
-
Imputointivaihe . Imputointi edustaa yleensä yhtä joukkoa uskottavia arvoja puuttuville tiedoille – moninkertainen imputointi edustaa useita uskottavien arvojen joukkoja . Kun käytetään moninkertaista imputointia, puuttuvat arvot tunnistetaan ja korvataan satunnaisotannalla uskottavien arvojen imputoinneista (täydennetyt tietokokonaisuudet). Useita täydennettyjä tietokokonaisuuksia luodaan jonkin valitun imputointimallin avulla . Viisi imputoitua tietokokonaisuutta on perinteisesti ehdotettu teoreettisin perustein riittäväksi, mutta 50 tietokokonaisuutta (tai enemmän) näyttäisi olevan parempi vaihtoehto imputointiprosessista aiheutuvan otantavaihtelun vähentämiseksi .
-
Viimeisteltyjen tietojen analyysivaihe (estimointi) . Haluttu analyysi suoritetaan erikseen jokaiselle tietokokonaisuudelle, joka syntyy imputointivaiheen aikana . Näin muodostetaan esimerkiksi 50 analyysitulosta.
-
Poolausvaihe. Kustakin valmistuneesta aineistosta saadut analyysitulokset yhdistetään yhdeksi moni-imputointitulokseksi . Painotettua meta-analyysiä ei tarvitse tehdä, koska kaikilla vaikkapa 50 analyysituloksella katsotaan olevan sama tilastollinen painoarvo.
On erittäin tärkeää, että imputointimalli ja analyysimalli ovat joko yhteensopivia tai imputointimalli on yleisempi kuin analyysimalli (esimerkiksi että imputointimalli sisältää enemmän riippumattomia kovariaatteja kuin analyysimalli) . Esimerkiksi jos analyysimallissa on merkittäviä interaktioita, imputointimallin tulisi sisällyttää myös ne , jos analyysimallissa käytetään muuttujan muunnettua versiota, imputointimallissa tulisi käyttää samaa muunnosta jne.
erilaisia moninkertaisen imputoinnin tyyppejä
Ei ole olemassa erityyppisiä moninkertaisen imputoinnin menetelmiä. Esittelemme ne niiden lisääntyvän monimutkaisuusasteen mukaan: 1) yhden arvon regressioanalyysi; 2) monotoninen imputointi; 3) ketjutetut yhtälöt tai Markov chain Monte Carlo (MCMC) -menetelmä. Seuraavissa kappaleissa kuvaamme näitä erilaisia moninkertaisia imputointimenetelmiä ja sitä, miten niiden välillä voidaan valita.
Yksiarvoinen regressioanalyysi sisältää riippuvaisen muuttujan ja satunnaistamisessa käytetyt ositusmuuttujat. Ositemuuttujat sisältävät usein keskusindikaattorin, jos kyseessä on monikeskustutkimus, ja yleensä yhden tai useamman säätömuuttujan, joilla on ennusteellista tietoa ja jotka korreloivat lopputuloksen kanssa. Jos käytetään jatkuvaa riippuvaista muuttujaa, mukaan voidaan sisällyttää myös riippuvan muuttujan lähtöarvo. Kuten kohdassa ”Syitä, miksi tilastollisia menetelmiä ei pitäisi käyttää puuttuvien tietojen käsittelyyn” mainitaan, jos vain riippuvalla muuttujalla on puuttuvia arvoja eikä apumuuttujia ole yksilöity, olisi suoritettava täydellinen tapausanalyysi eikä erityisiä menetelmiä pitäisi käyttää puuttuvien tietojen käsittelyyn. Jos apumuuttujat on tunnistettu, voidaan tehdä yhden muuttujan imputointi. Jos jatkuvan muuttujan perusmuuttujaan liittyy merkittäviä puuttuvia tietoja, täydellinen tapausanalyysi voi antaa vääristyneitä tuloksia. Siksi kaikissa tapauksissa tehdään yhden muuttujan imputointi (tarvittaessa apumuuttujien kanssa tai ilman niitä), jos vain perusmuuttuja puuttuu.
Jos sekä riippuvainen muuttuja että perusmuuttuja puuttuvat ja puuttuvuus on monotoninen, tehdään monotoninen imputointi. Oletetaan tietomatriisi, jossa potilaat esitetään riveillä ja muuttujat sarakkeilla. Tällaisen tietomatriisin puuttuvuuden sanotaan olevan monotoninen, jos sen sarakkeet voidaan järjestää uudelleen siten, että minkä tahansa potilaan kohdalla a) jos jokin arvo puuttuu, kaikki sen oikealla puolella olevat arvot puuttuvat myös, ja b) jos jokin arvo on havaittu, kaikki tämän arvon vasemmalla puolella olevat arvot ovat myös havaittuja . Jos puuttuvuus on monotoninen, moninkertaisen imputoinnin menetelmä on myös suhteellisen suoraviivainen, vaikka useammalla kuin yhdellä muuttujalla olisi puuttuvia arvoja . Tällöin on suhteellisen yksinkertaista imputoida puuttuvat tiedot käyttämällä peräkkäistä regressioimputointia, jossa puuttuvat arvot imputoidaan kullekin muuttujalle kerrallaan . Monet tilastopaketit (esimerkiksi STATA) voivat analysoida, onko puuttuvuus monotoninen vai ei.
Jos puuttuvuus ei ole monotoninen, moninkertainen imputointi suoritetaan käyttämällä ketjutettuja yhtälöitä tai MCMC-menetelmää. Apumuuttujat sisällytetään malliin, jos ne ovat saatavilla. Kuviossa 2 on esitetty yhteenveto siitä, miten eri moninkertaisen imputoinnin menetelmien välillä valitaan.
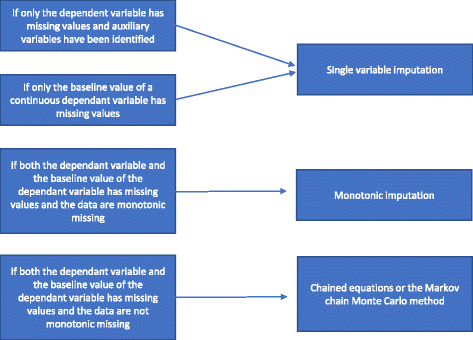
Virtauskaavio moninkertaisesta imputoinnista
Täysinformaation maksimilikelihood
Täysinformaation maksimilikelihood on eräs vaihtoehtoinen puuttuvan datan käsittelyyn soveltuva tapa . Maximum likelihood -estimoinnin periaatteena on estimoida lopputuloksen (Y) ja kovariaattien (X1,…, Xk) yhteisen jakauman parametrit, jotka, jos ne ovat totta, maksimoivat todennäköisyyden havaita ne arvot, jotka todellisuudessa havaitsimme . Jos tietyn potilaan arvot puuttuvat, saadaan todennäköisyys laskemalla tavanomainen todennäköisyys yhteen kaikkien puuttuvien tietojen mahdollisten arvojen yli edellyttäen, että puuttuvien tietojen mekanismia ei voida huomioida. Tätä menetelmää kutsutaan täyden informaation maksimiluotettavuudeksi .
Full information maximum likelihoodilla on sekä vahvuuksia että rajoituksia verrattuna moninkertaiseen imputaatioon.
Strengths of full information maximum likelihood compared to multiple imputation
- 1)
Se on yksinkertaisempi toteuttaa, ts. ei tarvitse käydä läpi eri vaiheita kuten moninkertaista imputointia käytettäessä.
- 2)
Moninkertaisesta imputoinnista poiketen täydellisen informaation maksimilikelihoodissa ei ole mahdollisia ongelmia imputointimallin ja analyysimallin yhteensopimattomuudesta (ks. ”Moninkertainen imputointi”). Moninkertaisen imputoinnin tulosten pätevyys on kyseenalainen, jos imputointimallin ja analyysimallin välillä on yhteensopimattomuutta tai jos imputointimalli on vähemmän yleinen kuin analyysimalli .
- 3)
Käytettäessä moninkertaista imputointia kaikki puuttuvat arvot kussakin luodussa tietokokonaisuudessa (imputointivaihe) korvataan satunnaisotannalla uskottavista arvoista . Näin ollen, ellei ”satunnaista siementä” ole määritetty, joka kerta kun moninkertainen imputaatioanalyysi suoritetaan, saadaan erilaisia tuloksia . Analyysit, joissa käytetään täyden informaation maksimiluotettavuutta samalle tietokokonaisuudelle, tuottavat samat tulokset joka kerta, kun analyysi suoritetaan, eivätkä tulokset näin ollen ole riippuvaisia satunnaislukusiemenestä. Jos satunnaisluvun siemenarvo kuitenkin määritellään tilastollisen analyysin suunnitelmassa, tämä ongelma voidaan ratkaista.
Limitations of full information maximum likelihood compared to multiple imputation
Limitations of full information maximum likelihood verrattuna moninkertaiseen imputaatioon, rajoituksena on se, että täyden informaation maksimaalisen likelihoodin käyttäminen on mahdollista vain käyttämällä erityisesti suunniteltuja ohjelmistoja . Suunniteltuja alustavia ohjelmistoja on kehitetty, mutta useimmissa niistä ei ole kaupallisesti suunniteltujen tilasto-ohjelmistojen (esimerkiksi STATA, SAS tai SPSS) ominaisuuksia. STATA:ssa (SEM-komennon avulla) ja SAS:ssa (PROC CALIS-komennon avulla) on mahdollista käyttää täyden informaation maksimiluotettavuutta, mutta vain silloin, kun käytetään jatkuvia riippuvaisia (tulos)muuttujia. Logistista regressiota ja Cox-regressiota varten ainoa kaupallinen paketti, joka tarjoaa täyden informaation maksimaalisen likelihoodin puuttuville tiedoille, on Mplus.
Potentiaalinen rajoitus täyden informaation maksimaalista likelihoodia käytettäessä on myös se, että taustalla voi olla oletus monimuuttujien normaalisuudesta. Monimuuttujaisen normaalisuusolettaman rikkomukset eivät kuitenkaan välttämättä ole niin merkittäviä, joten voi olla hyväksyttävää sisällyttää analyysiin binäärisiä riippumattomia muuttujia .
Olemme lisänneet lisätiedostoon 1 ohjelman (SAS), joka tuottaa täydellisen lelutietoaineiston, joka sisältää useita erilaisia analyysejä näistä tiedoista. Taulukot 1 ja 2 osoittavat tulosteet ja sen, miten eri menetelmät, jotka käsittelevät puuttuvia tietoja, tuottavat erilaisia tuloksia.
Paneeliarvojen regressioanalyysi
Paneeliaineisto sisältyy yleensä ns. laajaan datatiedostoon, jossa ensimmäinen rivi sisältää muuttujien nimet ja seuraavat rivit (yksi kutakin potilasta kohden) vastaavat arvot. Lopputulosta edustavat eri muuttujat – yksi kutakin suunniteltua, ajoitettua lopputuloksen mittausta varten. Tietojen analysoimiseksi tiedosto on muunnettava niin sanotuksi pitkäksi tiedostoksi, jossa on yksi tietue kutakin suunniteltua lopputulosmittausta kohden ja joka sisältää lopputulosarvon, mittausajankohdan ja kopion kaikista muista muuttujien arvoista lukuun ottamatta lopputulosmuuttujan arvoja. Jotta potilaan sisäiset korrelaatiot ajoitettujen lopputulosmittausten välillä säilyisivät, on yleinen käytäntö, että datatiedostosta tehdään moninkertainen laskenta sen laajassa muodossa, minkä jälkeen tuloksena saatu tiedosto analysoidaan sen jälkeen, kun se on muunnettu pitkään muotoon. Jatkuvien lopputulosarvojen analysointiin voidaan käyttää proc. mixed (SAS 9.4) ja muiden lopputulostyyppien analysointiin proc. glimmix (SAS 9.4). Koska nämä proseduurit soveltavat suoraa maksimilikelihood-menetelmää tulostietoihin, mutta jättävät huomiotta tapaukset, joista puuttuvat kovariaattiarvot, proseduureja voidaan käyttää suoraan silloin, kun vain riippuvaisen muuttujan arvot puuttuvat ja hyviä apumuuttujia ei ole käytettävissä. Muussa tapauksessa proc. mixed- tai proc. glimmix-menetelmää (riippuen siitä, kumpi on asianmukainen) olisi käytettävä moninkertaisen laskennan jälkeen. Vastaava lähestymistapa voi luonnollisesti olla mahdollinen muiden tilastopakettien avulla.
Tarkkuusanalyysit
Tarkkuusanalyysit voidaan määritellä joukoksi analyysejä, joissa tietoja käsitellään eri tavalla kuin ensisijaisessa analyysissä. Herkkyysanalyysit voivat osoittaa, miten ensisijaisessa analyysissä tehdyistä oletuksista poikkeavat oletukset vaikuttavat saatuihin tuloksiin. Herkkyysanalyysit olisi määriteltävä ja kuvattava etukäteen tilastollisessa analyysisuunnitelmassa, mutta ylimääräiset jälkikäteen tehtävät herkkyysanalyysit voivat olla perusteltuja ja päteviä. Kun puuttuvien arvojen mahdollinen vaikutus on epäselvä, suosittelemme seuraavia herkkyysanalyysejä:
-
Olemme jo kuvailleet parhaan ja huonoimman tapauksen herkkyysanalyysien käyttöä puuttuvien tietojen aiheuttaman epävarmuuden vaihteluvälin osoittamiseksi (ks. kohta Arvio siitä, pitäisikö puuttuvien tietojen käsittelyyn käyttää menetelmiä). Aiempi kuvauksemme parhaimman ja huonoimman tapauksen herkkyysanalyyseistä liittyi joko kaksijakoisen tai jatkuvan riippuvaisen muuttujan puuttuviin tietoihin, mutta näitä herkkyysanalyysejä voidaan käyttää myös silloin, kun tietoja puuttuu ositusmuuttujista, lähtötasoarvoista jne. Puuttuvien tietojen mahdollinen vaikutus olisi arvioitava kunkin muuttujan osalta erikseen, eli kullekin muuttujalle (riippuvainen muuttuja, lopputulosindikaattori ja ositusmuuttujat), josta puuttuu tietoja, olisi laadittava yksi parhaan ja yhden huonoimman tapauksen skenaario.
-
Jos päätetään käyttää esimerkiksi useita imputaatioita, näiden tulosten olisi oltava ensisijainen tulos kyseisestä lopputuloksesta. Jokaista ensisijaista regressioanalyysia olisi aina täydennettävä vastaavalla havaitun (tai käytettävissä olevan) tapauksen analyysillä.
Kun käytetään sekavaikutusmenetelmiä
Monikeskustutkimusasetelman käyttäminen on usein tarpeen, jotta voidaan rekrytoida riittävä määrä tutkimukseen osallistujia kohtuullisessa ajassa . Monikeskustutkimusasetelma tarjoaa myös paremman perustan tulosten myöhemmälle yleistämiselle . On osoitettu, että satunnaistetuissa kliinisissä tutkimuksissa yleisimmin käytetyt analyysimenetelmät toimivat hyvin pienellä määrällä keskuksia (analysoitaessa binäärisiä riippuvaisia tuloksia) . Kun keskuksia on suhteellisen paljon (50 tai enemmän), on usein optimaalista käyttää ”keskusta” satunnaisvaikutuksena ja käyttää sekavaikutusten analyysimenetelmiä. Usein on myös perusteltua käyttää sekavaikutusten analyysimenetelmiä analysoitaessa pitkittäisaineistoja. Joissakin tapauksissa voi olla perusteltua sisällyttää satunnaisvaikutuksen kovariaatti (esimerkiksi ”keskus”) kiinteän vaikutuksen kovariaattina imputointivaiheessa ja käyttää sitten analyysivaiheessa sekamallianalyysiä tai yleistettyjä estimointiyhtälöitä (GEE). Sekavaikutusmallin soveltaminen (jossa esimerkiksi ”keskusta” on satunnaisvaikutus) merkitsee kuitenkin sitä, että aineiston monikerroksinen rakenne on otettava huomioon moninkertaista imputointia mallinnettaessa. Tähän tarkoitukseen ei ole nyt suoraan saatavilla kaupallisia ohjelmistoja. Voidaan kuitenkin käyttää REALCOME-pakettia, joka voidaan liittää STATAan. Rajapinta vie puuttuvat arvot sisältävän datan STATAsta REALCOMiin, jossa imputointi tehdään ottaen huomioon datan monitasoinen luonne ja käyttäen MCMC-menetelmää, joka sisältää jatkuvat muuttujat ja joka latentin normaalimallin avulla mahdollistaa myös diskreetin datan asianmukaisen käsittelyn. Imputoidut tietokokonaisuudet voidaan tämän jälkeen analysoida STATAn ”mi estimate:” -komennolla, joka voidaan yhdistää STATAn ”mixed”-lauseeseen (jos kyseessä on jatkuva tulos) tai ”meqrlogit”-lauseeseen, jos kyseessä on binäärinen tai ordinaalinen tulos. Paneeliaineistoa analysoitaessa voidaan kuitenkin helposti joutua tilanteeseen, jossa aineisto sisältää kolme tai useampia tasoja, esimerkiksi mittaukset saman potilaan sisällä (taso 1), potilaat keskusten sisällä (taso 2) ja keskukset (taso 3) . Jotta ei tarvitsisi sekaantua melko monimutkaiseen malliin, joka voi johtaa konvergenssin puutteeseen tai epävakaaseen keskivirheeseen ja jota varten ei ole saatavilla kaupallisia ohjelmistoja, suosittelemme joko käsittelemään keskuksen vaikutusta kiinteänä (joko suoraan tai sen jälkeen, kun pienet keskukset on yhdistetty yhdeksi tai useammaksi sopivan kokoiseksi keskukseksi käyttäen tilastollisessa analyysisuunnitelmassa määriteltävää menettelyä) tai jättämään keskuksen pois kovariaattina. Jos satunnaistaminen on ositettu keskusten mukaan, jälkimmäinen lähestymistapa johtaa keskivirheiden vääristymiseen ylöspäin, mikä johtaa jokseenkin konservatiiviseen testimenettelyyn.