Lotka-Volterran yhtälöt kuvaavat ekologista saalistaja-pyydystäjän (tai loisen ja isännän) välistä saalistus- (tai loisen ja isännän) -mallia, jossa oletetaan, että, joukolle kiinteitä positiivisia vakioita 
(saaliin kasvunopeus), 
(nopeus, jolla saalistajat tuhoavat saalista), 
(saalistajien kuolemanopeus) ja 
(nopeus, jolla saalistajat lisääntyvät kuluttamalla saalista) pätevät seuraavat ehdot.
1. Saalispopulaatio 
kasvaa nopeudella 
(verrannollinen saaliin määrään), mutta saalistajat tuhoavat sen samanaikaisesti nopeudella 
(verrannollinen saaliin ja saalistajien lukumäärän tuloon).
2. Petopopulaatio 
pienenee nopeudella 
(verrannollinen petojen määrään), mutta kasvaa nopeudella 
(jälleen verrannollinen saaliin ja petojen lukumäärän tuloon).
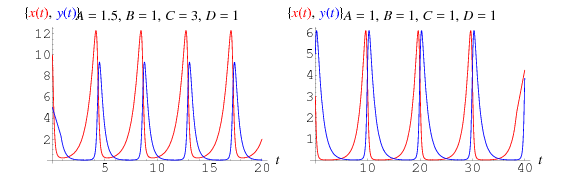
Tällöin saadaan kytketyt differentiaaliyhtälöt
 |
 |
 |
(1)
|
 |
 |
 |
(2)
|
ratkaisut, jotka on piirretty edellä, jossa saaliit on esitetty punaisella ja saalistajat sinisellä. Tällaisessa mallissa saaliskäyrä johtaa aina saalistajakäyrää.
Kriittisiä pisteitä esiintyy, kun 
, joten
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
Ainoa paikallaan oleva piste sijaitsee siis kohdassa 
.