Mitä eroa on koveralla ja koveralla?
Jos kuvailisimme koveran ja koveran eroa mahdollisimman yleisellä tavalla, sanoisimme, että mikä tahansa ontto, kulhon kaltainen esine on kovera, kun taas mikä tahansa rugby-palloa tai jalkapalloa muistuttava esine on muodoltaan kovera. Mutta ehkäpä kuperaa ja koveraa käytetään niin usein väärin siksi, että nämä kaksi sanaa eivät ole niin yksinkertaisia kuin haluaisimme niiden olevan.
Useimmat kielioppilähteet pitävät kiinni siitä, kuinka mnemoniikan käyttäminen on mahdollista kuperan ja koveran tulkitsemiseksi sanaluolan kautta. Vaikka ajatus siitä, että kovera liitetään tapahtumaan, jossa jokin ”luhistuu”, auttaa oppimaan pintapiirteistä, on hämmentävää liittää tämä ajatus kohti aiheita, joihin liittyy kuvaajia.
Ymmärtääksemme, miten kovera ja kupera eroavat toisistaan, meidän on opittava, miten kumpaakin termiä käytetään matematiikan, peilien, linssien ja lopulta luovan kirjoittamisen piirissä. Kun olet päättänyt, missä yhteydessä haluat käyttää sellaisia sanoja kuin kovera ja kupera, niiden teknisten näkökohtien oppiminen antaa sinulle enemmän varmuutta käyttää niitä arkipuheessa.

Mitä kovera tarkoittaa?
Koveraa käytetään adjektiivina tai substantiivina kuvaamaan esineen tai pinnan muotoa, joka on sisäänpäin kaareva tai ontto kuin kulho. Esimerkkejä concave-sanasta lauseessa ovat,
”She scooped the ice cream from the container, leaving a concave footprint.”
The Oxford Dictionary of Word Histories -sanakirjan mukaan sana concave on peräisin myöhäiskeskiajan englannista. Concave ja concavity tuottavat latinankielisen termin concavus (con- ja cavus), joka kääntyy ’yhdessä’ ja ’ontto’ (”Concave”, 110).
Synonyymejä concave ovat mm:
Dented, depressed, dished, hollow, indented, recessed, and sunken.
Antonyms of concave include:
Pullistuva, kovera, ulkoneva, ulkoneva, ulkoneva, ulkoneva.
Mitä tarkoittaa kovera?
Sana kovera eli koveruus on adjektiivi, joka kuvaa esinettä tai pintaa, joka on pyöristynyt tai kaareva. Esineistä puhuttaessa kuperan esineen keskipinta on leveämpi kuin sen ulkokulma. Esimerkkejä kuperasta lauseessa ovat,
”Putosin myrkkysumakkeeseen ja nyt minulla on punaisia, kuperia kuoppia ympäri ihoani.”
Synonyymit sanalle convex include:
kaareva, taivutettu, pullistunut, kohonnut.
Antonyms of convex include:
painunut, vajoava.
Koverat vs. koverat funktiot
Konveksinen funktio edustaa kuvaajassa jatkuvaa viivaa, jossa alueen keskipiste eli mediaani-kokonaisluku ei ylitä alueen keskiarvoa. Kovera funktio on koveran funktion täydellinen vastakohta, sillä jotta f(x) olisi kovera, f(x):n on oltava negatiivinen. Jotta erot tulisivat selvemmiksi, tässä on lyhyt yhteenveto termien vertailusta:
Konkaviili ylöspäin = kovera = kovera alaspäin
Konkaviili alaspäin = kovera = kovera ylöspäin
Konkavien ja koverien funktioiden välinen ero käy selvemmin ilmi, jos tarkastelemme kuvaajaa. Huomaa, kuinka kovera funktio avautuu ylöspäin, kun taas kovera funktio avautuu alaspäin.
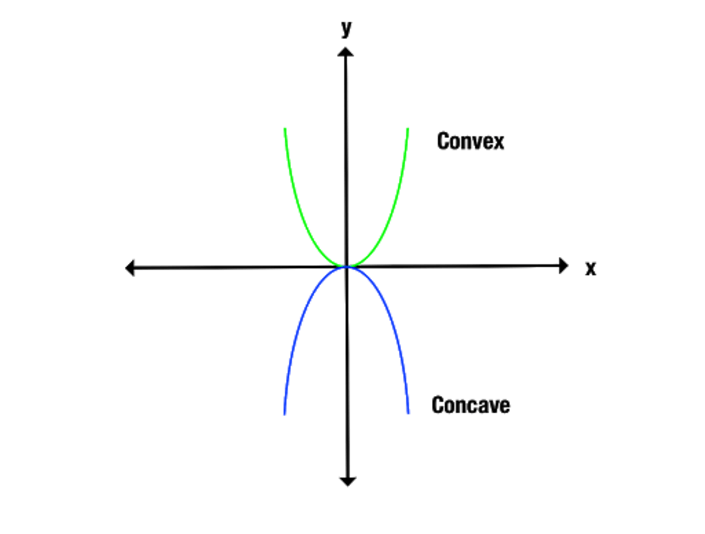
Toinen tapa tunnistaa koverat ja koverat funktiot on yhdistää kuvaajan pisteet x-akselia pitkin. Kovera funktio yhdistää vain kuvaajan alapuolella olevia viivoja, kun taas kovera funktio tuottaa vain kuvaajan yläpuolella olevia viivoja.
Voidaan lisäksi käyttää laskutoimitusta sen selvittämiseen, onko funktio kovera vai kovera. Jos f(x):n toinen derivaatta on suurempi kuin nolla, funktio on kupera. Mutta jos f(x):n toinen derivaatta on pienempi kuin nolla, funktio on kovera.
Kupera vs. kovera monikulmio
Ei paniikkia, mutta sanoja kupera ja kovera käytetään myös geometriassa. Kuperista ja koverista muodoista puhutaan useimmiten monikulmioista, jotka ovat muotoja, joissa on vähintään kolme sivua ja kulmaa.
Säännöllisiä monikulmioita on olemassa, joiden sivut ja kulmat ovat yhtä suuret, mutta kuperat ja koverat monikulmiot ovat hieman monimutkaisempia. Kupera monikulmio sisältää sisäkulmia, jotka ovat alle 180 astetta, kun taas koverat monikulmio sisältää yhden tai useamman sisäkulman, jotka ovat yli 180 astetta.
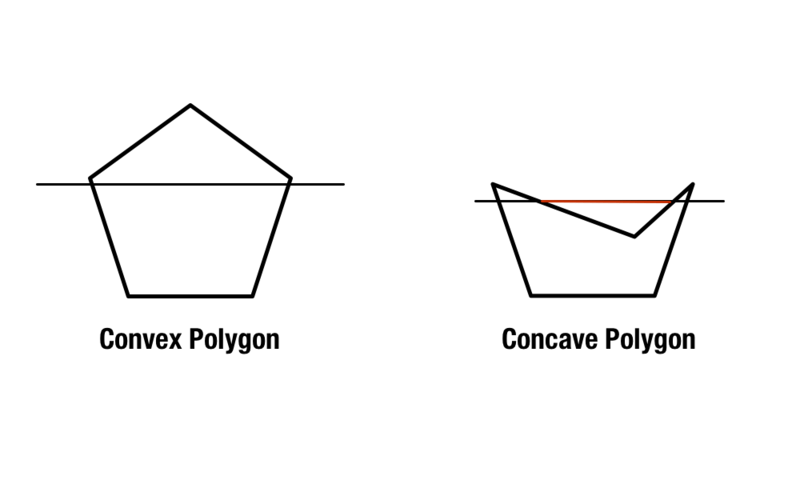
Toinen tapa tunnistaa koverat ja koverat monikulmiot on piirtää muodon poikki kaksi diagonaaliviivaa, jotka alkavat muodon kulmista. Jos jokainen viiva on muodon sisällä, muoto on kupera. Jos ainakin yksi viiva kulkee muodon ulkopuolella, se on kovera.
Koverat vs. kuperat peilit
Sanoja kovera ja kovera käytetään yleisesti puhuttaessa optisista esineistä, kuten peileistä ja linsseistä. Mikä tahansa kupera pinta työntyy ulospäin kuplan tavoin, mikä antaa vaikutelman leveydestä. Kuperia peilejä käytetään yleisesti parkkihalleissa, joissa kuljettajat tarvitsevat laajaa näkymää kulmien tai mahdollisten kuolleiden kulmien taakse.

Kovera peili sen sijaan on sisäänpäin kaareva ja tuottaa suurennetun heijastuksen, joka on ylösalaisin. Kuten Etelä-Walesin yliopiston fysiikan laitos osoitti, kuka tahansa, jolla on kiiltävä lusikka, voi testata tämän havainnon katsomalla omaa heijastustaan lusikassa. Lusikan koveralla pinnalla, josta poimit ruokasi, heijastuksesi vääristyy kapealla tavalla, ja näytät ylösalaisin. Mutta jos käännät lusikan kuperalle puolelle, heijastuksesi on pystyssä ja pienempi.
Heijastukset vaihtelevat niin suuresti kuperien ja koverien pintojen välillä, koska riippumatta siitä, kaarevatko pinnat ulospäin vai sisäänpäin, peili itsessään on osa palloa. Koska pallon pinta ei ole tasainen, sen pinnasta heijastuva valo kulkee eri matkoja ennen kuin se koskettaa peiliä.
Riippuen siitä, mihin pinnan osaan valo koskettaa, valonsäde voi heijastua läheisistä pinnoista tuottaen tarkemman näkyvyysalueen. Tästä syystä lusikan sisäpintaa tarkasteltaessa saatetaan nähdä vain sen heijastuma, joka on lähimpänä lusikan pintaa – vaikka se näyttäisikin silti pienemmältä. Lisäksi, jos asetat sormen lusikan sisälle, peilipinta voi tuottaa kaksi tai kolme eri heijastusta samanaikaisesti.
Kovera linssi vs. kupera linssi
Koveria ja kuperia linssejä on arkipäiväisissä esineissä, kuten silmälaseissa, piilolaseissa, kiikareissa ja kaukoputkissa. Samoin kuin kuperien ja koverien peilien valon heijastumisen taustalla oleva tiede, on olemassa kaavat siitä, miten valo kulkee koverien ja kuperien linssien läpi tuottaen näkyvän kuvan.

Kuperat linssit
Manocha Akatemian mukaan kuperia linssejä kutsutaan konvergoituviksi linsseiksi, koska ne pystyvät tuottamaan pienennettyjä, suurennettuja tai sisäänpäin kääntyneitä kuvia. Se, kuinka tarkasti kuva näkyy kuperan linssin läpi, riippuu siitä, kuinka lähellä kohde on linssin polttopistettä. Kaikissa kuperissa linsseissä on symmetriset polttopisteet linssin kummallakin puolella.
Kuinka tarkasti kohde syntyy kuperan linssin läpi, ennustetaan kolmen periaatteen avulla:
PERIAATE 1: Jokainen kuperan linssin läpi kulkeva valonsäde on yhdensuuntainen pääakselin kanssa, joka on pallomaisen linssin absoluuttisen keskipisteen kautta kulkeva keskiviiva. Kun valo koskettaa linssiä, valo taittuu ja kulkee toisella puolella olevan polttopisteen läpi. Läpikulkevat valonsäteet, jotka ovat pääakselin suuntaisia, kulkevat linssin edessä olevan kohteen yläpuolella.
PERIAATE 2: Jokainen valonsäde, joka kulkee kuperan linssin keskipisteen läpi, jatkuu suorana linssin toisella puolella.
Periaate 3: Mikä tahansa valonsäde, joka on kulkenut polttopisteen läpi samalla puolella kuin kohde, taittuu linssiin osuessaan ja muuttuu pääakselin suuntaiseksi toisella puolella.
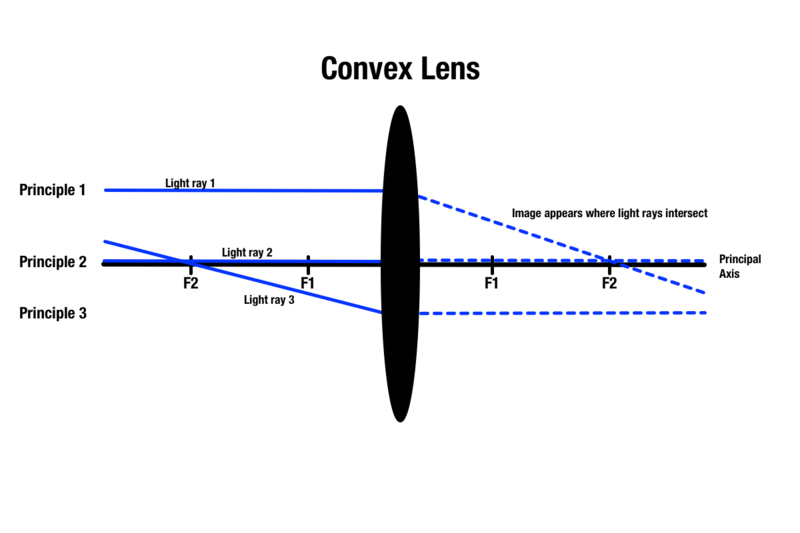
Vaikka kuperan linssin läpi kulkevan kuvanlaadun ennustamiseen on kolme periaatetta, vain kahta periaatetta voidaan soveltaa kohteeseen sädekuviota piirtäessä. Mitkä tahansa kaksi periaatetta tuottavat linssin toisella puolella valon leikkauspisteen, joka osoittaa alueen, jossa kohteen kuva näkyy.
Mitä kauempana esine on kuperasta linssistä, sitä pienempi kuva näkyy toisella puolella, ja mitä lähempänä esine on kuperaa linssiä, sitä suurempi se näkyy. Kohde, joka sijaitsee lähimmän polttopisteen takana, tuottaa suuremman kuvan kohteen taakse. Kuten Manocha Academy huomauttaa, tämäntyyppistä linssin suurennusta käytetään optisissa välineissä, kuten suurennuslaseissa.
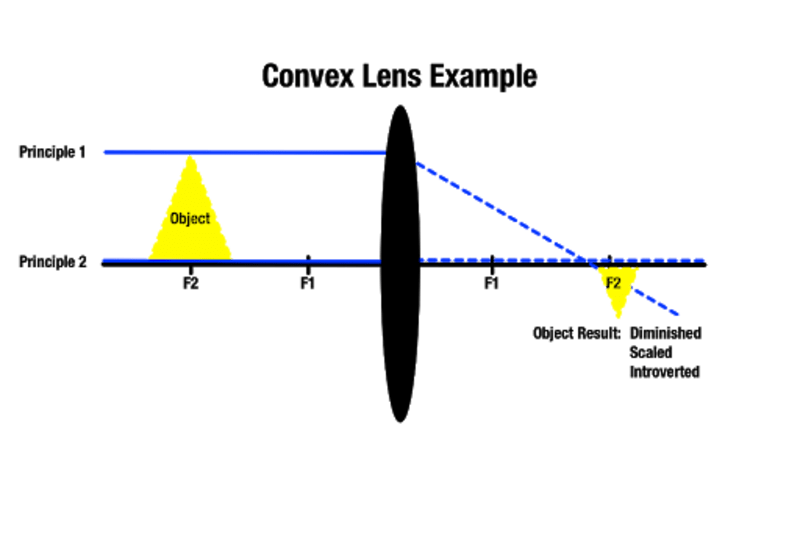
Sitä riippuen, missä polttopisteessä esine sijaitsee, on mahdollista tuottaa likimääräisen kokoinen kuva. On myös mahdollista luoda todellisia kuvia, jotka eivät näy, jos ohi kulkevat valonsäteet eivät koskaan risteä, koska ne ovat toisella puolella yhdensuuntaisia. Tällöin tuotettu kuva on olemassa äärettömän kaukana.
Koverat linssit
Jokainen kovera linssi on halkaisijaltaan paksumpi ja keskeltä ohuempi, koska kovera linssi on sisäänpäin kaareva. Koverien linssien muodon ansiosta valo leviää, kun se koskettaa linssiä, jolloin virtuaaliset kohteet näyttävät pienemmiltä. Koveran linssin kyky levittää valoa tekee siitä ihanteellisen linssin taskulamppujen kaltaisiin työkaluihin, joissa keskitettyä valonlähdettä voidaan käyttää laajemmalla pinta-alalla.
Koverat linssit tuottavat kuvia kolmella periaatteella, jotka muistuttavat kuperia linssejä:
PERIAATE 1: Mikä tahansa valonsäde, joka kulkee kohteen yläpuolella ja pääakselin suuntaisesti, taittuu linssin kohdatessa ja näyttää siltä kuin se tulisi lähimmän polttopisteen suunnasta.
PERIAATE 2: Mikä tahansa valonsäde, joka kulkee koveran linssin keskipisteen läpi, läpäisee sen ilman taittumista.
PERIAATE 3: Mikä tahansa valonsäde, joka suuntautuu koveran linssin toisella puolella olevaan polttopisteeseen, taittuu ja muuttuu pääakselin suuntaiseksi.
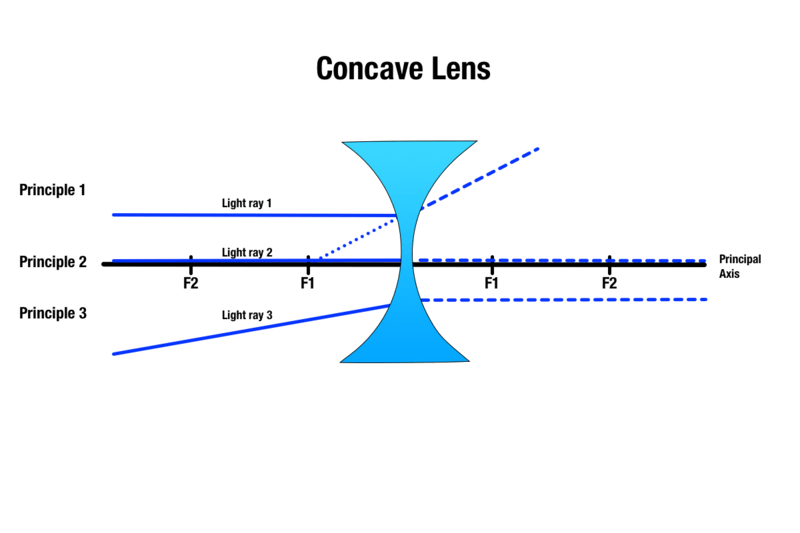
Vaikka kohteen kuvan koko vaihtelee sen mukaan, mikä on kohteen etäisyys koverasta linssistä, syntyvä kuva on aina virtuaalinen, pystysuora, pienempi ja se ilmestyy linssin samalle puolelle kuin kohde.
Kovera vs. kovera kirjoituksessa
Sanat kovera ja kovera ovat toistensa vastakohtia, ja ne kuvaavat olennaisesti esineiden tai pintojen muotoa samalla tavalla kuin asetamme vastakkain sellaiset sanat kuin:
- Pieni vs. pieni. big
- Pitkä vs. lyhyt
- Lyhyt vs. leveä
- Pyöreä vs. litteä
Koska kovera ja kovera ovat teknisiä sanoja, niiden käyttäminen kuvaavasti proosassa voi tuottaa satunnaiselle yleisölle metaforisemman tai abstraktimman tulkinnan. Tämä tarkoittaa sitä, että jos kirjoittajat päättävät käyttää koveraa tai kuperaa sanaa niiden tyypillisen käytön ulkopuolella, kirjoittajan on päätettävä, kuinka selkeää hänen kirjoituksensa on tarkoitus olla.
Harkitse adjektiivia
Esimerkillinen esimerkki koveran tai kuperan käytöstä kirjallisuudessa on amerikkalaisen kirjailijan David Foster Wallacen (tai lyhyesti DFW) kirjoitukset. DFW on tunnettu monimutkaisesta ja teknisestä kirjoitustyylistään– ja kyllä, hän käytti kuperaa ja koveraa kuvaamaan substantiiveja useita kertoja. Wallace käyttää koveraa ja kuperaa seuraavissa esimerkeissä:
”Kädenjälkeni oli kunnossa, mutta en ollut suuri enkä nopea, minulla oli lähes kovera rintakehä ja niin ohuet ranteet, että pystyin rannekorjaamaan ne peukalolla ja pikkusormella…”.
– ”Tennis, trigonometria, Tornadot: A Midwestern Boyhood,” Harper’s Magazine.
”…nuken silmät, jotka avautuvat sydännyörin vedolla, koverat siellä missä minä olen kupera.”
– ”Order and Flux in Northampton,” Conjunctions.
DFW:n esimerkkien käyttämisen tarkoituksena ei ole pelkästään osoittaa, miten kirjailijat ovat käyttäneet kuperaa tai koveraa matemaattisen kontekstin ulkopuolella, vaan pikemminkin se, että kirjailijat voivat pohtia, onko teknisten tai abstraktien termien käyttäminen hyödyllistä, jotta he voivat viestiä selkeästi yleisölleen.
Ensimmäisessä DFW-esimerkissä koveran käyttö on järkevää, koska hän kuvaa jonkin asian rakennetta. Mutta koveran ja kuperan käyttäminen kuvaamaan ei-objektiivisia substantiiveja, kuten tunteita tai ajatuksia, pyrkii hämärtämään sen merkityksen, mitä yritämme selittää. Toisessa DFW:n esimerkissä kuljetaan hienolla linjalla, kun käytetään kuperaa ja koveraa, koska niiden käyttö on sekä kirjaimellista että metaforista.
FAQ:
Mikä on funktio?
Funktio on suoran yhtälö kuvaajassa. Funktiot ovat erilaisia jokaisella kuvaajan suoralla, mutta ne ovat yleisessä muodossa,
f(x) = x + 1
Millä tahansa suoran funktiolla riippuvainen muuttuja on tyypillisesti f(x), kun taas mitä tahansa tuntematonta muuttujaa funktion sisällä kutsutaan riippumattomaksi muuttujaksi.
Mikä on toimialue?
Toimialue on riippumattomien muuttujien joukko kuvaajassa, joka vastaa suoran funktiota. Alueet ovat tärkeitä ymmärtää, koska ne paikantavat tietyt pisteet kaaviossa, joka vastaa mitä tahansa yhtälön todellista tulosta.
Mikä on alue?
Minkä tahansa funktion alue edustaa mitä tahansa mahdollista arvoa kuvaajan x- tai y-akselilla, joka tuottaa riippuvalle muuttujalle kelvollisen arvon. Kaikki pienimmät ja suurimmat kokonaisluvut tunnistetaan korvaamalla muuttujat x- tai y-akselilla.
Mikä on väli?
Väli on joukko lukuja, jotka edustavat viivan kokonaislukuja eli toimialuetta. Suljettu intervalli sisältää suoran kaksi äärellistä pistettä, joissa suoraa ei enää ole kokonaislukualueen ulkopuolella. Avoin väli on joukko kokonaislukuja, jotka eivät edusta suoran toimialueen absoluuttista loppua.
Testaa itsesi!
Katso, kuinka hyvin ymmärrät kuperan ja koveran eron seuraavilla monivalintakysymyksillä:
- Katsellessasi kiiltävää lusikkaa huomaat peilikuvasi olevan ylösalaisin. Lusikan pinta on _________ pinta.
a. Kupera
b. Peili
c. Kovera
d. Metalli - Graafisten funktioiden kannalta kuperaa funktiota kutsutaan joskus:
a. Kovera ylöspäin
b. Kupera alaspäin
c. Kovera alaspäin
d. A ja B - Mikä seuraavista ei kuvaa koveraa pintaa:
a. Ontto puolipallo
b. Silmälinssi
c. Murokulho
d. Puolipallo - Mikä seuraavista ei kuvaa kuperaa pintaa:
a. Family Guyn hahmo Stewie
b. Pallo
c. Parkkihallin peili
d. Jalkapallo - Mikä seuraavista muodoista ei voi olla kovera monikulmio:
a. Pentagon
b. Kuusikulmio
c. Kolmio
d. Octagon
Vastaukset
- C: Kovera
- D: A ja B
- D: Puolipallo
- B: Pallo
- C: Kolmio
Lähteet:
- Bourne, M. ”Domain and Range of a Function”. Interactive Mathematics, Jan. 4, 2019.
- ”Concave”. Merriam-Websterin sanakirja, 2019.
- ”Concave”. The Oxford Dictionary of Word Histories, toim. Chantrell, 2002, s. 110.
- ”Concave and Convex Mirrors”. Manocha Academy, YouTube, 2019.
- ”Kovera linssi: Definition & Uses.” Study.com, 2019.
- ”Convex”. Merriam-Websterin sanakirja, 2019.
- ”Convex and Concave Lenses”. Manocha Academy, YouTube, 2019.
- ”Matematiikka / Monikulmioiden ymmärtäminen”. Learnhive Inc. 2018.
- ”Heijastus koverasta peilistä.” UNSW Physics, YouTube, 2017.
- Wallace, D.F. ”Tennis, trigonometria, tornadot: A Midwestern Boyhood.” Harper’s Magazine, 1991.
- Wallace, D.F. ”Järjestys ja virtaus Northamptonissa”. Conjunctions, 1991.
- Weisstein, Eric W. ”Kovera funktio”. MathWorld-A Wolfram Web Resource, n.d.
- Weisstein, Eric W. ”Convex Function”. MathWorld-A Wolfram Web Resource, n.d.
Sanalaskuri on dynaaminen online-työkalu, jota käytetään sanojen, merkkien, lauseiden, kappaleiden ja sivujen reaaliaikaiseen laskemiseen sekä oikeinkirjoituksen ja kieliopin tarkistamiseen.