Esittely
Tällä sivulla tarkastellaan jatkuvuusyhtälöä, joka pakottaa massan säilymisen Eulerin analyysissä. Tämä ei ole varsinaisesti materiaalin käyttäytymisen kuvaus, mutta tuloksena saatua yhtälöä käytetään usein identiteettinä materiaalin käyttäytymistä kuvaavien konstitutiivisten mallien algebrallisessa käsittelyssä. Se on siis tarkistamisen arvoinen. Se on keskeinen myös nestevirtauksen analyysissä, koska klassiset nesteanalyysit eivät voi olla Lagrangen analyysejä, koska kaikkien nestehiukkasten sijainnit \(t = 0\) ovat tuntemattomia.
Massan säilyminen
Jatkuvuusyhtälö kuvastaa sitä, että massa säilyy missä tahansa muussa kuin ydinvoimaisessa jatkuvuusmekaniikan analyysissä. Yhtälö kehitetään laskemalla yhteen nopeus, jolla massa virtaa kontrollitilavuuden sisään ja ulos, ja asettamalla sisään tuleva nettovirtaus yhtä suureksi kuin massan muutosnopeus tilavuuden sisällä. Tämä on esitetty seuraavassa kuvassa.
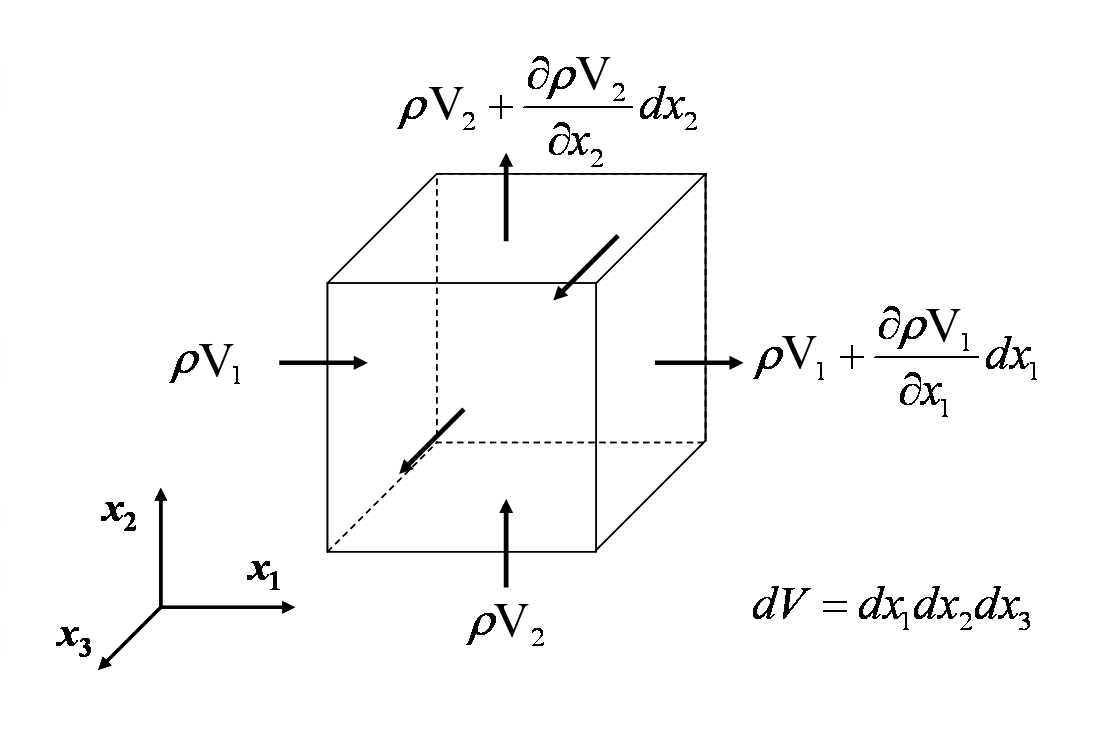
Edifferentiaalisen säätötilavuuden sisään- ja ulosmenevien massavirtojen yhtälöstä saadaan
\
Termien poistaminen ja jakaminen \(dx_1 dx_2 dx_3\). saadaan
\
ja uudelleen järjestämällä saadaan
\
Tämä voidaan lyhyesti kirjoittaa muodossa
\

Tärkeitä kohtia
Nämä ovat lopullisia, täydelliset ja yleisimmät muodot jatkuvuusyhtälöstä, joka toteuttaa massan säilymisen. Se pätee kaikkiin aineisiin,ei vain nesteisiin. Se pätee siis myös kiinteisiin aineisiin. Huomaa, että se on yksi skalaariyhtälö ja luonteeltaan eulerilainen, koska gradienttiehdot ovat \({\partial \over \partial x_i}\), eivät \({\partial \over \partial X_i}\).
Voidaan miettiä, onko tämän eulerilaisen yhtälön eulerilaiselle muodolle olemassa lagrangilainen vastine. On olemassa. Se kirjoitetaan yleensä muotoon
\
Tässä todetaan yksinkertaisesti, että massan differentiaalisen kappaleen deformoituneessa tilassa\(\rho \, dV\) on oltava yhtä suuri kuin sen alkuperäinen arvo\(\rho_o dV_o\) deformoitumattomassa tilassa.
Jatkuvuusyhtälöllä on useita erikoistapauksia.Ensimmäinen esiintyy silloin, kun virtaus on tasaista. Tällöin derivaatta ajan suhteen on nolla, jolloin jäljelle jää.
\\
Toinen erikoistapaus on kokoonpuristumattomuus, eli, \(\rho = \)vakio.Tällöin derivaatta ajan suhteen on nolla, ja \(\rho\) voidaan poistaa yhtälöstä, jolloin jäljelle jää vain
\
Tämä tulos on niin yksinkertainen, että se laajennetaan usein pois.
\
Huomaa, että tämä ei ole muuta kuin \(\text{tr}({\bf D}) = 0\) kokoonpuristumattomien aineiden tapauksessa.

Materiaalin derivaatta
Seuraava on huomionarvoinen, koska sen avulla tiheys- ja nopeusvektori voidaan erottaa toisistaan. Ensimmäiseksi sovelletaan jatkuvuusyhtälön divergenssitermiin tuotossääntöä.
\
Ja sitten huomataan, että\({\partial \rho \over \partial t} + {\bf v} \cdot \nabla \rho\)on vain tiheyden aineellinen derivaatta,\({D \rho \over D t}\).
Siten jatkuvuusyhtälö voidaan kirjoittaa myös
\
Jos aine on kokoonpuristumatonta, \(\rho\) ei voi muuttua, joten\( {D \rho \over D t} \) on oltava nolla, jolloin
\
Ja sitten jaetaan läpi \(\rho\) (koska se ei ole nolla), jolloin saadaan
\

Jatkuvuusyhtälö Esimerkki
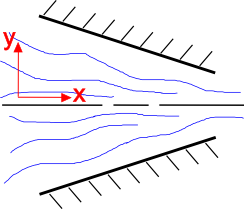
On intuitiivista, että nesteen virtaus kiihtyy poikkipinta-alan pienentyessä, kuten oikealla näkyy. Jatkuvuusyhtälö selittää tämän. Tarkastellaan kokoonpuristumattoman nesteen kaksiulotteista, tasaista virtauskenttää.Jatkuvuusyhtälö tälle tilanteelle on
\
Aloita tarkastelemalla virtauksen y-komponenttia, \(v_2\). Konvergoivan suuttimen geometria pakottaa \(v_2\)-komponentin virtaamaan ylöspäin, kun \(y \lt 0\) ja alaspäin, kun \(y \gt 0\). Joten \(v_2 \gt 0\) kun\(y \lt 0\) ja \(v_2 \lt 0\) kun \(y \gt 0\).
Tämän nettovaikutus on, että \({\partial v_2 \over \partial x_2} \lt 0\)konvergoituvassa suuttimessa.
Mutta jatkuvuusyhtälö määrää, että kahden osittaisderivaatan summan on oltava nolla. Joten jos toinen on pienempi kuin nolla, niin
\
Ja tämä tarkoittaa, että nestevirtauksen täytyy olla kiihtyvä.