Introductory Business Statistics

Harkitse seuraavaa aineistoa.
4; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 10

Tämä datajoukko voidaan esittää seuraavalla histogrammilla. Jokaisen intervallin leveys on yksi, ja jokainen arvo sijaitsee intervallin keskellä.

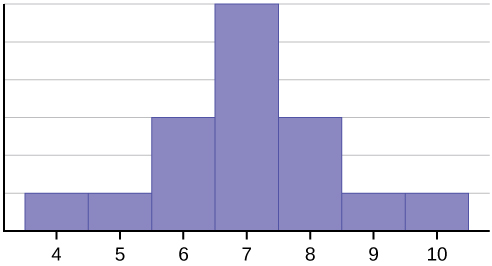
Histogrammi esittää datan symmetristä jakaumaa. Jakauma on symmetrinen, jos histogrammin johonkin kohtaan voidaan piirtää pystysuora viiva siten, että pystysuoran viivan vasemmalla ja oikealla puolella olevat muodot ovat toistensa peilikuvia. Näiden tietojen keskiarvo, mediaani ja moodi ovat kukin seitsemän. Täysin symmetrisessä jakaumassa keskiarvo ja mediaani ovat samat. Tässä esimerkissä on yksi moodi (unimodaalinen), ja moodi on sama kuin keskiarvo ja mediaani. Symmetrisessä jakaumassa, jossa on kaksi moodia (bimodaalinen), molemmat moodit olisivat eri kuin keskiarvo ja mediaani.

Datan histogrammi: 4566677778 ei ole symmetrinen. Oikeanpuoleinen puoli näyttää ”lohkaistulta” verrattuna vasemmanpuoleiseen. Tällaista jakaumaa kutsutaan vasemmalle vinoksi, koska se on vetäytynyt vasemmalle. Voimme muodollisesti mitata jakauman vinoutta aivan kuten voimme matemaattisesti mitata datan keskipainoa tai sen yleistä ”nopeutta”. Vinouden matemaattinen kaava on: . Mitä suurempi poikkeama nollasta on, sitä suurempi on vinous. Jos vinous on negatiivinen, jakauma on vinossa vasemmalle, kuten (kuvassa). Positiivinen vinouden mitta osoittaa oikeanpuoleista vinoutta, kuten (kuva).

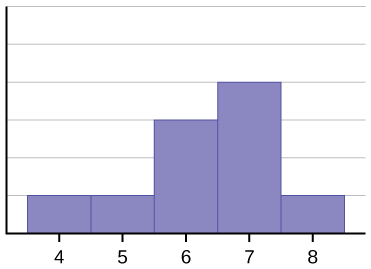
Keskiarvo on 6,3, mediaani on 6,5 ja moodi on seitsemän. Huomaa, että keskiarvo on pienempi kuin mediaani, ja molemmat ovat pienempiä kuin moodi. Sekä keskiarvo että mediaani heijastavat vinoumaa, mutta keskiarvo heijastaa sitä enemmän.

Aineiston histogrammi: 67777888910, ei myöskään ole symmetrinen. Se on vinoutunut oikealle.

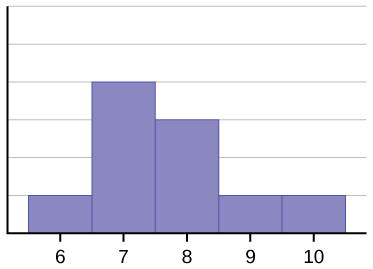
Keskiarvo on 7,7, mediaani on 7,5 ja moodi on seitsemän. Kolmesta tilastosta keskiarvo on suurin, kun taas moodi on pienin. Jälleen kerran keskiarvo heijastaa vinoutta eniten.

Yhteenvetona voidaan todeta, että yleensä jos aineiston jakauma on vinoutunut vasemmalle, keskiarvo on pienempi kuin mediaani, joka on usein pienempi kuin moodi. Jos aineiston jakauma on vinoutunut oikealle, moodi on usein pienempi kuin mediaani, joka on pienempi kuin keskiarvo.

Kuten keskiarvon, mediaanin ja moodin, ja kuten kohta näemme, varianssin, osalta on olemassa matemaattisia kaavoja, jotka antavat meille tarkkoja mittoja näistä aineiston jakauman ominaisuuksista. Kun tarkastelemme jälleen vinoutta koskevaa kaavaa, huomaamme, että se on aineiston keskiarvon ja yksittäisten havaintojen välinen suhde kuutioituina.

missä on aineiston otoksen keskihajonta, , ja on aritmeettinen keskiarvo ja on otoskoko.

Formallisesti aritmeettinen keskiarvo tunnetaan jakauman ensimmäisenä momenttina. Toinen tarkasteltava momentti on varianssi, ja vinous on kolmas momentti. Varianssi mittaa aineiston neliöeroja keskiarvosta ja vinous mittaa aineiston kuutioeroja keskiarvosta. Varianssi ei voi koskaan olla negatiivinen luku, mutta vinouden mitta voi olla negatiivinen, ja näin määritetään, onko aineisto vino oikealle vai vasemmalle. Normaalijakauman vinous on nolla, ja kaikkien symmetristen tietojen vinouden pitäisi olla lähellä nollaa. Vinouden negatiiviset arvot osoittavat, että tiedot ovat vinossa vasemmalle, ja positiiviset arvot osoittavat, että tiedot ovat vinossa oikealle. Vasemmalle vino tarkoittaa, että vasen häntä on pitkä suhteessa oikeaan häntään. Vastaavasti oikealle vino tarkoittaa, että oikea häntä on pitkä suhteessa vasempaan häntään. Vinous kuvaa jakauman epäsymmetrian astetta keskiarvon ympärillä. Vaikka keskiarvo ja keskihajonta ovat mitallisia suureita (siksi otamme varianssin neliöjuuren ) eli niillä on samat yksiköt kuin mitattavilla suureilla , vinous määritellään tavanomaisesti siten, että se on dimensioton. Se on puhdas luku, joka luonnehtii vain jakauman muotoa. Vinouden positiivinen arvo merkitsee jakaumaa, jonka epäsymmetrinen häntä ulottuu ulospäin kohti positiivisempaa X:ää, ja negatiivinen arvo merkitsee jakaumaa, jonka häntä ulottuu ulospäin kohti negatiivisempaa X:ää. Nollan mittainen vinouden arvo merkitsee symmetristä jakaumaa.

Vinoudesta ja symmetriasta tulee tärkeitä, kun keskustelemme todennäköisyysjakaumista myöhemmissä luvuissa.