The Toom-Cook Algorithm
Tässä opimme nerokkaan sovelluksen hajota ja hallitse -algoritmille yhdistettynä lineaarialgebraan suurten lukujen kertomiseen nopeasti. Ja johdatus big-O-notaatioon!
Tämä tulos on itse asiassa niin intuition vastainen, että suuri matemaatikko Kolmogorov arveli, ettei näin nopeaa algoritmia ole olemassa.
Osa 0: Pitkä kertolasku on hidasta kertolaskua. (Ja johdatus Big-O-notaatioon)
Me kaikki muistamme, että koulussa opeteltiin kertolaskua. Itse asiassa minulla on tunnustus tehtävänä. Muistakaa, että täällä ei saa tuomita 😉
Koulussa meillä oli ”märkäleikkejä”, kun satoi liikaa leikkiä leikkikentällä. Sillä välin kun muut (normaalit/hauskuutta rakastavat/positiivinen-adjektiivi-valinta) lapset pelasivat pelejä ja pelleilivät, minä otin joskus paperiarkin ja kerroin isoja lukuja yhteen, ihan vain huvin vuoksi. Pelkkää laskemisen iloa! Meillä oli jopa kertolaskukilpailu, ”Super 144”, jossa meidän oli kerrottava 12 kertaa 12 numeroa (1-12) sisältävä ruudukko mahdollisimman nopeasti. Harjoittelin tätä uskonnollisesti siinä määrin, että minulla oli omia valmiita harjoituslomakkeita, jotka valokopioin ja joita käytin vuorotellen. Lopulta sain aikani laskettua 2 minuuttiin ja 1 sekuntiin, jolloin raapustamisen fyysinen rajani oli saavutettu.
Huolimatta tästä kertolaskun pakkomielteestä minulle ei koskaan tullut mieleen, että voisimme tehdä sen paremmin. Vietin niin monta tuntia kertomalla, mutta en koskaan yrittänyt parantaa algoritmia.
Asettele vaikka 103:n kertomista luvulla 222.
Laskemme 2 kertaa 3 kertaa 1 +2 kertaa 0 kertaa 10 + 2 kertaa 1 kertaa 100 + 20 kertaa 3 kertaa 1 + 20 kertaa 0 kertaa 10 + 20 kertaa 1 kertaa 100 = 22800
Yleisesti n-numeroisille luvuille kertomiseen kuluu O(n²)-operaatiota. Iso-O-merkintä tarkoittaa, että jos kuvaamme operaatioiden lukumäärää n:n funktiona, n²-termi on oikeastaan se, millä on merkitystä. Muoto on pohjimmiltaan kvadraattinen.
Tänään toteutamme kaikki lapsuuden haaveemme ja parannamme tätä algoritmia. Mutta ensin! Big-O odottaa meitä.
Big-O
Katsokaa kahta alla olevaa kuvaajaa

Kysy matemaatikolta, ”ovatko x² ja x²+x^(1/3) samat?”, ja hän luultavasti oksentaa kahvikuppiinsa, alkaa itkeä ja mutisee jotain topologiasta. Ainakin se oli minun reaktioni (aluksi), ja tuskin tiedän topologiasta mitään.
Okei. Ne eivät ole sama asia. Mutta meidän tietokoneemme ei välitä topologiasta. Tietokoneet eroavat suorituskyvyltään niin monella tavalla, etten osaa edes kuvailla, koska en tiedä tietokoneista mitään.
Mutta höyryjyrästä ei kannata hienosäätää. Jos kaksi funktiota kasvaa suurilla tuloarvoillaan samaa suuruusluokkaa, niin käytännön kannalta se sisältää suurimman osan oleellisesta informaatiosta.
Yllä olevasta kuvaajasta näemme, että kaksi funktiota näyttävät melko samanlaisilta suurilla tuloarvoilla. Mutta samoin x² ja 2x² ovat samanlaisia – jälkimmäinen on vain kaksi kertaa niin suuri kuin edellinen. Kun x = 100, toinen on 10 000 ja toinen 20 000. Tämä tarkoittaa, että jos pystymme laskemaan toisen, pystymme todennäköisesti laskemaan toisenkin. Kun taas funktio, joka kasvaa eksponentiaalisesti, vaikkapa 10^x, hetkellä x = 100 on jo paljon paljon suurempi kuin maailmankaikkeuden atomien lukumäärä. (10¹⁰⁰ >>>>> 10⁸⁰, joka on googlaukseni* mukaan arvio, Eddingtonin luku, maailmankaikkeuden atomien määrästä).
*Tosiasiassa käytin DuckDuckGo:ta.
Kokonaislukujen kirjoittaminen polynomeiksi on sekä hyvin luonnollista että hyvin luonnotonta. Kirjoittaminen 1342 = 1000 + 300 + 40 + 2 on hyvin luonnollista. Kirjoittaminen 1342 = x³+3x²+4x + 2, jossa x = 10, on hieman outoa.
Yleisesti, oletetaan, että haluamme kertoa kaksi suurta lukua, jotka kirjoitetaan b-perustassa ja joissa on n numeroa kummassakin. Kirjoitetaan kumpikin n-numeroinen luku polynomina. Jos jaamme n-numeroisen luvun r osaan, tässä polynomissa on n/r-termiä.
Olkoon esimerkiksi b = 10, r = 3 ja lukumme on 142 122 912
Voimme muuttaa tämän muotoon
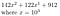
Tämä toimii hyvin, kun r = 3 ja luvussamme, joka on kirjoitettu 10:n perusluvulla, on 9 numeroa. Jos r ei jaa n:ää täydellisesti, voimme vain lisätä nollia eteen. Tämäkin käy parhaiten ilmi esimerkin avulla.
27134 = 27134 + 0*10⁵ = 027134, jonka esitämme muodossa
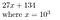
Miksi tämä voisi olla hyödyllistä? Löytääksemme polynomin P kertoimet, jos polynomi on järjestysasteeltaan N, niin ottamalla siitä näytteitä N+1 pisteessä voimme määrittää sen kertoimet.
Jos esimerkiksi polynomista x⁵ + 3x³ +4x-2, joka on järjestysluku 5, otetaan näytteet 6 pisteessä, voimme silloin laskea koko polynomin.
Intuitiivisesti järjestysluvun 5 polynomilla on 6 kerrointa: kerroin 1, x, x², x², x², x², x², x², x². Annettuna 6 arvoa ja 6 tuntematonta, voimme selvittää arvot.
(Jos osaat lineaarialgebraa, voit käsitellä x:n eri potensseja lineaarisesti riippumattomina vektoreina, tehdä matriisin kuvaamaan informaatiota, invertoida matriisin ja voilà)
Polynomien näytteenotto kertoimien määrittämiseksi (Valinnainen)
Tässä tarkastelemme hieman perusteellisemmin logiikkaa, joka on taustalla otettaessa näytteenotto polynomista sen kertoimien päättämiseksi. Voit vapaasti siirtyä seuraavaan kappaleeseen.
Näytämme, että jos kaksi polynomia, joiden aste on N, ovat yhtäpitäviä N+1 pisteessä, niiden täytyy olla samoja. Ts. N+1 pistettä määrittää yksikäsitteisesti polynomin, jonka aste on N.
Harkitaan polynomia, jonka aste on 2. Tämä on muotoa P(z) = az² +bz + c. Algebran perustavanlaatuisen lauseen mukaan – häpeilemätön pistoke tässä, käytin useita kuukausia kootakseni todisteen tästä ja kirjoittaakseni sen sitten tänne – tämä polynomi voidaan faktoroida. Se tarkoittaa, että voimme kirjoittaa sen muotoon A(z-r)(z-w)
Huomaa, että kohdissa z = r ja z = w polynomi saa arvon 0. Sanomme, että w ja r ovat polynomin juuria.
Nyt näytämme, että P(z):llä ei voi olla enempää kuin kaksi juurta. Oletetaan, että sillä on kolme juurta, joita kutsumme w, r, s. Faktorisoimme sitten polynomin. P(z) = A(z-r)(z-w). Sitten P(s) = A(s-r)(s-w). Tämä ei ole yhtä kuin 0, koska nollasta poikkeavien lukujen kertominen antaa nollasta poikkeavan luvun. Tämä on ristiriita, koska alkuperäinen oletuksemme oli, että s on polynomin P juuri.
Tätä väitettä voidaan soveltaa polynomiin, jonka järjestys on N, olennaisesti samalla tavalla.
Esitettäköön nyt, että kaksi polynomia P ja Q, joiden järjestys on N, ovat yhtäpitäviä N+1 pisteessä. Silloin, jos ne ovat erilaisia, P-Q on järjestyksen N polynomi, joka on 0 N+1 pisteessä. Edellisen mukaan tämä on mahdotonta, koska järjestyksen N polynomilla on korkeintaan N juurta. Näin ollen oletuksemme on täytynyt olla väärä, ja jos P ja Q ovat yhtäpitäviä N+1 pisteessä, ne ovat sama polynomi.
Näkeminen on uskomista: A Worked Example
Katsotaanpa todella suurta lukua, jota kutsumme p:ksi. 10:n emäksessä p on 24 numeroa pitkä (n=24), ja jaetaan neljään osaan (r=4). n/r = 24/4 = 6
p = 292,103,243,859,143,157,364,152.
Ja olkoon sitä kuvaava polynomi nimeltään P,
P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152
mikäli P(10⁶) = p.
Koska tämän polynomin asteluku on 3, niin voimme laskea kaikki kertoimet ottamalla näytteenottoa neljästä kohdasta. Tutkitaan, mitä tapahtuu, kun otamme siitä näytteen muutamasta kohdasta.
- P(0) = 364,152
- P(1) = 1,043,271
- P(-1) = 172,751
- P(2) = 3,962,726
Silmiinpistävää on se, että näissä kaikissa on 6 tai 7 numeroa. Tämä verrattuna siihen, että p:ssä on alunperin 24 numeroa.
Kerrotaan p:llä q:llä. Olkoon q = 124,153,913,241,143,634,899,130, ja
Q(x) = 124,153 x³ + 913,241 x²+143,634 x + 899,130
Laskutoimitusten t=pq laskeminen saattaisi olla kamalaa. Mutta sen sijaan, että tekisimme sen suoraan, yritämme laskea t:n polynomiesityksen, jota nimitämme T. Koska P on polynomi, jonka järjestys on r-1=3, ja Q on polynomi, jonka järjestys on r-1=3, T on polynomi, jonka järjestys on 2r-2=6.
T(10⁶) = t = pq
T(10⁶) = P(10⁶)Q(10⁶)
Temppu on siinä, että laskemme T:n kertoimet sen sijaan, että kertoisimme suoraan p:n ja q:n yhteen. Silloin T(1⁰⁶):n laskeminen on helppoa, koska kertoaksemme 1⁰⁶:lla pistämme vain 6 nollaa taaksepäin. Kaikkien osien yhteenlasku on myös helppoa, koska yhteenlasku on tietokoneille hyvin edullinen toimenpide.
T:n kertoimien laskemiseksi meidän on otettava siitä näyte 2r-1 = 7 pisteessä, koska se on polynomi, jonka järjestys on 6. Haluamme todennäköisesti valita pieniä kokonaislukuja, joten valitsemme
- T(0)=P(0)Q(0)= 364,152*899,130
- T(1)=P(1)Q(1)= 1,043,271*2,080,158
- T(2)=P(2)Q(2)= 3,962,726*5,832,586
- T(-1)=P(-1)Q(-1)= 172751*1544584
- T(-2)=P(-2)Q(-2)= -1,283,550*3,271,602
- T(3)=P(-3)Q(-3)= -5,757,369*5,335,266
Huomaa P(-3), Q(-3), P(2), Q(2) jne. koko… Nämä kaikki ovat lukuja, joissa on noin n/r = 24/4 = 6 numeroa. Osa on 6-numeroisia, osa 7-numeroisia. Kun n kasvaa, tämä approksimaatio muuttuu yhä järkevämmäksi.
Tähän mennessä olemme pelkistäneet ongelman seuraaviin vaiheisiin tai algoritmiin:
(1) Lasketaan ensin P(0), Q(0), P(1), Q(1) jne. (vähän kustannuksia aiheuttava toimenpide)
(2) Saadaksemme T(x):n arvot, jotka ovat 2r-1= 7, meidän on nyt kerrottava keskenään arvot, jotka ovat likimääräisesti kooltaan noin 2r-1 lukumäärää, jotka ovat pituudeltaan n/r-luokan numeroita. Meidän on nimittäin laskettava P(0)Q(0), P(1)Q(1), P(-1)Q(-1) jne. (Kallis toimenpide)
(3) Rekonstruoi T(x) datapisteistämme. (Vähäkustannuksinen toiminto: mutta otetaan huomioon myöhemmin).
(4) Arvioi rekonstruoidun T(x):n avulla T(10⁶) tässä tapauksessa
Tämä johtaa hienosti analyysiin tämän lähestymistavan suoritusajasta.
Käyntiaika
Yllä olevasta saimme selville, että kun jätämme väliaikaisesti huomiotta edulliset toimet (1) ja (3), kahden n-numeroisen luvun kertomisen kustannukset Toomin algoritmilla noudattavat:
>
Tämän näimme työstetystä esimerkkitehtävästä. Jokaisen P(0)Q(0):n, P(1)Q(1):n jne. kertominen maksaa T(n/r), koska kerromme kaksi noin n/r pituista lukua. Meidän on tehtävä tämä 2r-1 kertaa, koska haluamme ottaa näytteen T(x):stä – joka on järjestysluvultaan 2r-2 polynomi – 2r-1:ssä paikassa.
Miten nopeaa tämä on? Voimme ratkaista tällaisen yhtälön eksplisiittisesti.

Nyt jäljelle jää enää joitakin sotkuista algebraa
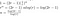
Matriisin kertomisesta (”uudelleen kokoamisesta”) aiheutui joitakin muita kustannuksia, ja yhteenlaskusta, emme voi oikeastaan sanoa, että ratkaisumme on tarkka ajoaika, joten sen sijaan päätellään, että olemme löytäneet ajoajan iso-O:n
Optimoimalla r
Tämä ajoaika riippuu edelleen r:stä. Korjaa r, niin olemme valmiit. Mutta uteliaisuutemme ei ole vielä tyydytetty!
Kun n kasvaa suureksi, haluamme löytää likimain optimaalisen arvon valitsemallemme r:lle. Toisin sanoen haluamme valita r:n arvon, joka muuttuu eri n-arvoilla.
Keskeistä tässä on se, että r:n vaihdellessa meidän on kiinnitettävä huomiota uudelleenkokoonpanon kustannuksiin – matriisin, joka suorittaa tämän operaation, kustannus on O(o(r²)). Kun r oli kiinteä, meidän ei tarvinnut kiinnittää huomiota tähän, koska kun n kasvoi suureksi r:n ollessa kiinteä, n:n sisältämät termit määrittivät sen kasvun, kuinka paljon laskentaa tarvittiin. Koska optimaalinen valintamme r:lle kasvaa n:n kasvaessa, emme voi enää jättää tätä huomiotta.
Tämä ero on ratkaiseva. Aluksi analyysimme valitsi r:n arvon, ehkä 3, ehkä 3 miljardia, ja tarkasteli sitten big-O:n kokoa n kasvaessa mielivaltaisen suureksi. Nyt tarkastelemme käyttäytymistä, kun n kasvaa mielivaltaisen suureksi ja r kasvaa n:n mukana jollakin määrittelemällämme nopeudella. Tämä näkökulman muutos tarkastelee O(r²):tä muuttujana, kun taas kun r pidettiin kiinteänä, O(r²) oli vakio, vaikkakin sellainen, jota emme tienneet.
Päivitämme siis analyysimme aiemmasta:
>
>
jossakin O(r²) kuvaa uudelleenkokoontumisverkkomatriisin kustannuksia. Haluamme nyt valita jokaiselle n:n arvolle sellaisen r:n arvon, joka suunnilleen minimoi tämän lausekkeen. Minimoimiseksi kokeilemme ensin differentioida r:n suhteen. Tämä antaa hieman vastenmielisen näköisen lausekkeen

Normaalisti minimipisteen löytämiseksi asetamme derivaatan yhtä suureksi kuin 0. Mutta tällä lausekkeella ei ole mukavaa minimiä. Sen sijaan löydämme ”riittävän hyvän” ratkaisun. Käytämme r = r^(sqrt(logN)) vierasarvona. Graafisesti tämä on melko lähellä minimiä. (Alla olevassa kaaviossa 1/1000-kerroin on siinä, jotta kuvaaja näkyy kohtuullisessa mittakaavassa)
Alla olevassa kaaviossa on T(N)-funktiomme, joka on skaalattu vakiolla, punaisella. Vihreä viiva on kohdassa x = 2^sqrt(logN), joka oli vierasarvomme. ”x” korvaa ”r:n”, ja jokaisessa kolmessa kuvassa käytetään eri N:n arvoa.



Tämä on minusta aika vakuuttavaa, että valintamme oli hyvä. Tällä r:n valinnalla voimme liittää sen ja nähdä, miten algoritmimme lopullinen iso-O:

jossa yksinkertaisesti liitimme arvomme r:lle ja käytimme approksimaatiota log(2r-1)/log(r):lle, joka on hyvin tarkka suurille r:n arvoille.
Paljonko parannus?
Ehkä se, etten huomannut tätä algoritmia, kun olin pikkupoikana kertomista tekemässä, oli ehkä kohtuullista. Alla olevassa kuvaajassa annan big-O-funktiomme kertoimeksi 10 (havainnollistamistarkoituksessa) ja jaan sen x²:llä (koska alkuperäinen lähestymistapa kertolaskuun oli O(n²). Jos punainen viiva pyrkii 0:aan, se osoittaisi, että uusi suoritusaikamme on asymptoottisesti parempi kuin O(n²).
Ja tosiaan, vaikka funktion muoto osoittaa, että lähestymistapamme on lopulta nopeampi, ja lopulta se on paljon nopeampi, joudumme odottamaan, kunnes meillä on lähes 400-numeroisia pitkiä lukuja, ennen kuin tämä pitää paikkansa! Vaikka kerroin olisi vain 5, lukujen pitäisi olla noin 50 numeroa pitkiä, jotta nopeus paranisi.

Kymmenvuotiaalle itselleni 400-numeroisten lukujen kertolasku olisi hieman hankalaa! Myös funktioni eri rekursiivisten kutsujen seuraaminen olisi hieman pelottavaa. Mutta tietokoneelle, joka tekee tehtävää tekoälyn tai fysiikan alalla, tämä on yleinen ongelma!
Miten syvällinen tämä tulos on?
Pidän tässä tekniikassa siitä, että se ei ole rakettitiedettä. Se ei ole kaikkein älyttömin matematiikka, joka on koskaan löydetty. Jälkikäteen ajateltuna se vaikuttaa ehkä itsestäänselvyydeltä!
Tässä on kuitenkin matematiikan nerokkuus ja kauneus. Luin, että Kolmogorov arveli eräässä seminaarissa, että kertolasku on pohjimmiltaan O(n²). Kolmogorov periaatteessa keksi paljon modernia todennäköisyysteoriaa ja analyysia. Hän oli yksi 1900-luvun matemaattisista suuruuksista. Silti kun kyse oli tästä toisiinsa liittymättömästä alasta, kävi ilmi, että hänen ja kaikkien muiden nenän alla odotti kokonainen tietopaketti, joka istui aivan hänen ja kaikkien muidenkin nenän alla!
Itse asiassa ”Jaa ja hallitse” -algoritmit tulevat nykyään mieleen melko nopeasti, koska niitä käytetään niin yleisesti. Mutta ne ovat tietokonevallankumouksen tuote siinä mielessä, että vasta valtavan laskentatehon myötä ihmismielet ovat keskittyneet nimenomaan laskennan nopeuteen matematiikan omana tutkimisen arvoisena osa-alueena.
Sentähden matemaatikot eivät ole halukkaita hyväksymään Riemannin hypoteesin paikkansa pitäväksi vain siksi, että se näyttää siltä, että se voisi olla totta, tai että P ei ole yhtä suuri kuin NP vain siksi, että se näyttää todennäköisimmältä. Matematiikan ihmeellinen maailma säilyttää aina kykynsä hämmentää odotuksemme.
Itse asiassa voit löytää vielä nopeampia tapoja kertoa. Nykyiset parhaat lähestymistavat käyttävät nopeita Fourier-muunnoksia. Mutta säästän sen toiselle päivälle 🙂
Kertokaa ajatuksenne alhaalla. Olen hiljattain Twitterissä nimellä ethan_the_mathmo, voit seurata minua täältä.
Löysin tämän ongelman käyttämästäni ihanasta fyysikoiden Mooren ja Mertensin kirjasta ”The Nature of Computation”, jossa yksi ongelmista ohjaa sinua analysoimaan Toomin algoritmia.