Graafeja on erityyppisiä riippuen kärkipisteiden määrästä, särmien määrästä, keskinäisestä yhteenkytkettävyydestä ja niiden yleisestä rakenteesta. Käsittelemme tässä luvussa vain muutamia tiettyjä tärkeitä graafityyppejä.
Nollagraafi
Graafia, jossa ei ole yhtään särmää, kutsutaan nollagraafiksi.
Esimerkki

Yllä olevassa graafissa on kolme kärkeä nimeltä ’a’, ’b’ ja ’c’, mutta niiden välillä ei ole yhtään särmää. Näin ollen se on nollagraafi.
Triviaaligraafi
Graafia, jossa on vain yksi huippu, kutsutaan triviaaligraafiksi.
Esimerkki
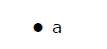
Yllä esitetyssä graafissa on vain yksi huippu ’a’, jossa ei ole muita reunoja. Näin ollen se on triviaaligraafi.
Ei-suuntautunut graafi
Ei-suuntautunut graafi sisältää särmiä, mutta särmät eivät ole suunnattuja.
Esimerkki
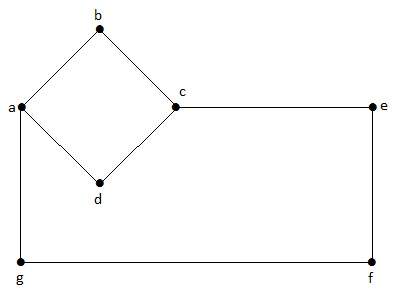
Tässä kuvaajassa ’a’, ’b’, ’c’, ’d’, ’e’, ’f’, ’g’ ovat kärkipisteitä ja ’ab’, ’bc’, ’cd’, ’da’, ’ag’, ’gf’, ’ef’ ovat kuvaajan reunoja. Koska kyseessä on suuntaamaton graafi, särmät ”ab” ja ”ba” ovat samat. Samoin muutkin reunat katsotaan samalla tavalla.
Suuntautunut graafi
Suuntautuneessa graafissa jokaisella reunalla on suunta.
Esimerkki
Yllä olevassa graafissa on seitsemän kärkeä ’a’, ’b’, ’c’, ’d’, ’e’, ’f’ ja ’g’ sekä kahdeksan reunaa ’ab’, ’cb’, ’dc’, ’ad’, ’ec’, ’fe’, ’gf’ ja ’ga’. Koska kyseessä on suunnattu graafi, jokaisessa reunassa on nuoli, joka osoittaa sen suunnan. Huomaa, että suunnatussa graafissa ’ab’ on eri kuin ’ba’.
Yksinkertainen graafi
Graafia, jossa ei ole silmukoita eikä yhdensuuntaisia särmiä, sanotaan yksinkertaiseksi graafiksi.
-
Yksittäisessä graafissa, jossa on ’n’ kärkeä, voi olla enimmillään ’nC2’ särmää, missä ’nC2’ = ’n(n – 1)/2’.
-
Mahdollisten yksinkertaisten graafien lukumäärä, joissa on ’n’ kärkeä = 2nc2 = 2n(n-1)/2.
Esimerkki
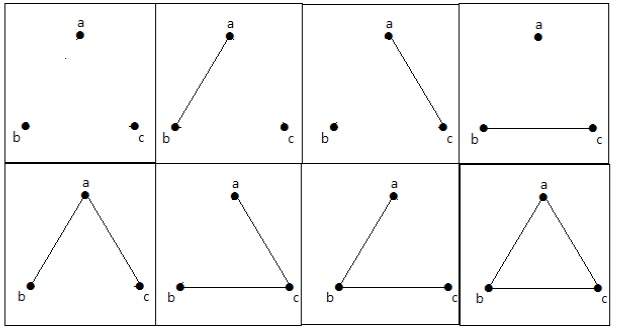
Oheisessa graafissa on 3 kärkeä, joissa on 3 särmää, mikä on maksimissaan ilman rinnakkaisia reunoja ja silmukoita. Tämä voidaan todistaa käyttämällä yllä olevia kaavoja.
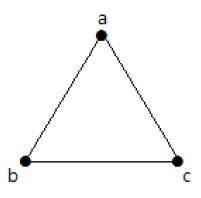
Särmien maksimimäärä, kun n=3 kärkeä –
nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
Yksinkertaisten graafien maksimimäärä, kun n=3 kärkeä –
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
Nämä kahdeksan graafia ovat seuraavat –
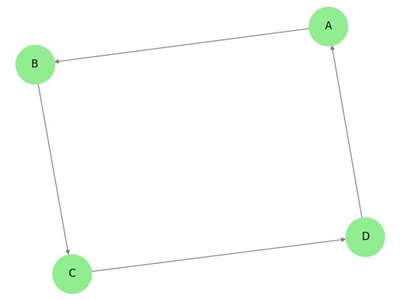
Yhteenliitetty graafi
Graafia G sanotaan yhteenliitetyksi (connected graph), jos jokaisen kärkiparin välissä kulkee polku. Jokaista graafin kärkeä kohti on oltava vähintään yksi reuna. Jotta voidaan sanoa, että se on yhteydessä johonkin toiseen pisteeseen reunan toisella puolella.
Esimerkki
Oheisessa graafissa jokaisella pisteellä on oma reuna, joka on yhteydessä toiseen reunaan. Näin ollen se on kytkeytynyt graafi.
Kytkeytymätön graafi
Graafi G on kytkeytymätön, jos se ei sisällä vähintään kahta kytkeytynyttä kärkeä.
Esimerkki 1
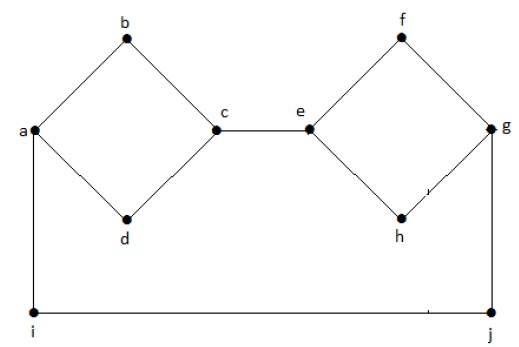
Oheinen kuvaaja on esimerkki epäyhtenäisestä kuvaajasta, jossa on kaksi komponenttia, joista toisessa on a-, b-, c-, d-pisteet ja toisessa e-, f-, g-, h-pisteet.
Kaksi komponenttia ovat toisistaan riippumattomia eivätkä ole kytköksissä toisiinsa. Siksi sitä kutsutaan irralliseksi graafiksi.
Esimerkki 2
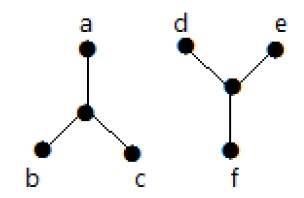
Tässä esimerkissä on kaksi riippumatonta komponenttia, a-b-f-e ja c-d, jotka eivät ole yhteydessä toisiinsa. Kyseessä on siis epäyhtenäinen graafi.
Regulaarinen graafi
Graafin G sanotaan olevan säännöllinen, jos sen kaikilla kärkipisteillä on sama aste. Jos graafissa jokaisen kärjen aste on ’k’, kutsutaan graafia ’k-säännölliseksi graafiksi’.
Esimerkki
Seuraavissa graafeissa kaikilla kärjillä on sama aste. Näitä kuvaajia kutsutaan siis säännöllisiksi kuvaajiksi.
Kummassakin kuvaajassa kaikilla kärkipisteillä on aste 2. Niitä kutsutaan 2-regulaarisiksi graafeiksi.
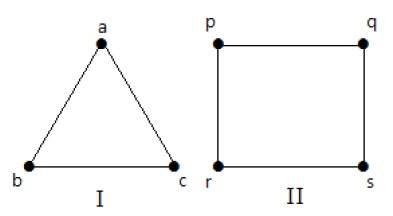
Täydellinen graafi
Yksinkertaista graafia, jossa on ’n’ keskinäistä kärkeä, kutsutaan täydelliseksi graafiksi ja sitä merkitään ’Kn’. Graafissa kärkipisteellä tulee olla särmiä kaikkien muiden kärkipisteiden kanssa, silloin sitä kutsutaan täydelliseksi graafiksi.
Muilla sanoilla, jos kärkipiste on yhteydessä kaikkiin muihin kärkipisteisiin graafissa, silloin sitä kutsutaan täydelliseksi graafiksi.
Esimerkki
Seuraavissa graafeissa, jokainen graafin kärkipiste on yhteydessä kaikkiin jäljellä oleviin kärkipisteisiin grafiikissa, lukuun ottamatta itseään.
Graafissa I,
| a | b | c | ||
|---|---|---|---|---|
| a | Ei ole kytketty | Kytketty | Kytketty | |
| b | Kytketty | Ei kytketty | Kytketty | |
| c | Kytketty | Kytketty | Kytketty | Ei kytketty |
Graafissa II,
| p | q | r | s | ||
|---|---|---|---|---|---|
| p | Ei kytketty | Kytketty | Kytketty | Kytketty | Kytketty |
| q | Kytketty | Ei kytketty | Kytketty | Kytketty | |
| r | Kytketty | Kytketty | Ei kytketty | Kytketty | |
| s | Kytketty | Kytketty | Kytketty | Kytketty | Ei… Connected |
Cycle Graph
Yksinkertaista graafia, jossa on ’n’ kärkeä (n >= 3) ja ’n’ särmää, kutsutaan sykligraafiksi, jos kaikki sen särmät muodostavat syklin, jonka pituus on ’n’.
Jos graafin jokaisen kärjen aste on kaksi, sitä kutsutaan syklegraafiksi.
Notaatio – Cn
Esimerkki
Tarkastellaan seuraavia graafeja –
-
Graafi I:ssä on 3 kärkeä, joissa on 3 särmää, jotka muodostavat syklin ’ab-bc-ca’.
-
Graafissa II on 4 kärkeä ja 4 särmää, jotka muodostavat syklin ’pq-qs-sr-rp’.
-
Graafissa III on 5 kärkeä ja 5 särmää, jotka muodostavat syklin ’ik-km-ml-lj-ji’.
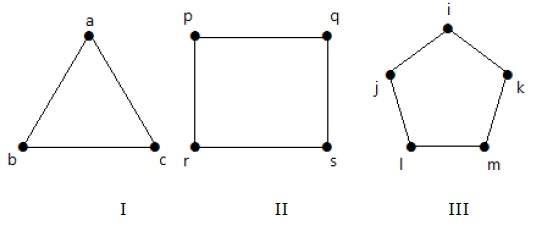
Siten kaikki annetut graafit ovat sykligraafeja.
Pyörägraafi
Pyörägraafi saadaan sykligraafista Cn-1 lisäämällä siihen uusi kärki. Tätä uutta kärkeä kutsutaan keskipisteeksi, joka on yhteydessä kaikkiin Cn:n kärkipisteisiin.
Notaatio – Wn
No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)
Esimerkki
Tarkastellaan seuraavia graafeja. Ne ovat kaikki pyörän graafeja.
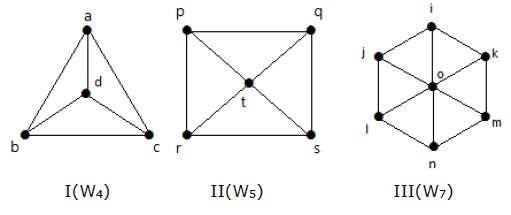
Graafissa I se saadaan C3:sta lisäämällä keskelle piste, jonka nimi on ’d’. Sitä merkitään nimellä W4.
Number of edges in W4 = 2(n-1) = 2(3) = 6
Graafissa II se saadaan C4:stä lisäämällä keskelle piste nimeltä ’t’. Sitä merkitään seuraavasti: W5.
Number of edges in W5 = 2(n-1) = 2(4) = 8
Kuvaajassa III se saadaan C6:sta lisäämällä keskelle huippu nimeltä ”o”. Sitä merkitään nimellä W7.
Number of edges in W4 = 2(n-1) = 2(6) = 12
Syklinen graafi
Graafia, jossa on vähintään yksi sykli, kutsutaan sykliseksi graafiksi.
Esimerkki
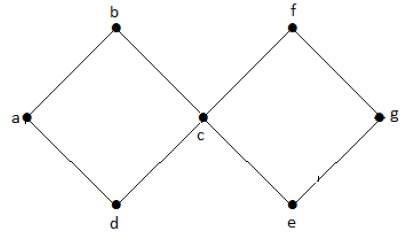
Yllä olevassa esimerkkigraafissa on kaksi sykliä a-b-c-d-a ja c-f-g-e-c. Näin ollen sitä kutsutaan sykliseksi graafiksi.
Asyklinen graafi
Graafia, jossa ei ole syklejä, kutsutaan asykliseksi graafiksi.
Esimerkki
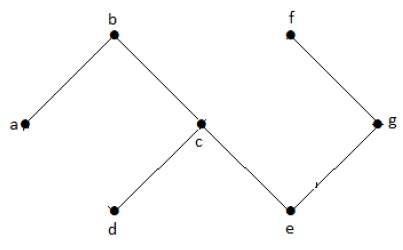
Yllä olevassa esimerkkigraafissa meillä ei ole yhtään sykliä. Näin ollen se on ei-syklinen graafi.
Kaksijakoinen graafi
Yksinkertaista graafia G = (V, E), jossa on pistejako V = {V1, V2}, kutsutaan kaksijakoiseksi graafiksi, jos jokainen E:n särmä yhdistää V1:n pisteen V2:n pisteeseen.
Yleisesti kaksijakoisessa graafissa on kaksi kärkijoukkoa, sanokaamme V1 ja V2, ja jos piirretään särmä, sen pitäisi yhdistää mikä tahansa joukon V1 kärkipiste mihin tahansa joukon V2 kärkipisteeseen.
Esimerkki
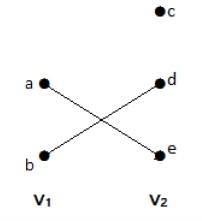
Tässä kuvaajassa on havaittavissa kaksi kärkijoukkoa – V1 ja V2. Tässä kaksi särmää nimeltä ’ae’ ja ’bd’ yhdistävät kahden joukon V1 ja V2 kärkipisteet.
Täydellinen kaksiosainen graafi
Kaksiosainen graafi ’G’, G = (V, E), jonka osio V = {V1, V2} on sanotaan täydelliseksi kaksiosaiseksi graafiksi, jos jokainen V1:n huippu on yhdistetty kaikkiin V2:n huippuihin.
Yleisesti täydellinen kaksijakoinen graafi yhdistää jokaisen joukon V1 pisteen jokaiseen joukon V2 pisteeseen.
Esimerkki
Seuraava graafi on täydellinen kaksijakoinen graafi, koska siinä on särmät, jotka yhdistävät jokaisen joukon V1 pisteen jokaiseen joukon V2 pisteeseen.
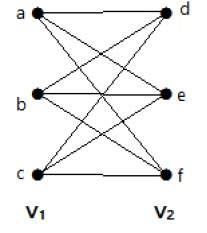
Jos |V1| = m ja |V2| = n, niin täydellistä kaksijakoista graafia merkitään nimellä Km, n.
-
Km,n:llä on (m+n) kärkeä ja (mn) särmää.
-
Km,n on säännöllinen graafi, jos m=n.
Yleisesti täydellinen kaksiosainen graafi ei ole täydellinen graafi.
Km,n on täydellinen graafi, jos m=n=1.
Särmien maksimimäärä kaksijakoisessa graafissa, jossa on n kärkeä, on
Jos n=10, K5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25
Vastavasti K6, 4=24
K7, 3=21
K8, 2=16
K9, 1=9
Jos n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20
Samoin K6, 3=18
K7, 2=14
K8, 1=8
’G’ on kaksiosainen graafi, jos ’G’:ssä ei ole yhtään parittoman pituista sykliä. Kaksijakoisen graafin erikoistapaus on tähtigraafi.
Tähtigraafi
Täydellinen kaksijakoinen graafi, jonka muoto on K1, n-1, on tähtigraafi, jolla on n-pistettä. Täydellinen kaksiosainen graafi on täydellinen kaksiosainen graafi, jos yksi ainoa huippu kuuluu yhteen joukkoon ja kaikki loput huippujoukot kuuluvat toiseen joukkoon.
Esimerkki
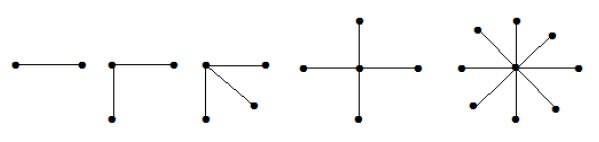
Yllä olevissa graafeissa ’n’ kärkipisteestä kaikki ’n-1’ kärkipisteet ovat yhteydessä yhteen ainoaan kärkipisteeseen. Näin ollen se on muodossa K1, n-1, jotka ovat tähtigraafeja.
Graafin komplementti
Olkoon ’G-’ yksinkertainen graafi, jossa on joitakin kärkipisteitä kuten ’G:ssä’, ja särmä {U, V} on ’G-’:ssä, jos särmä ei ole G:ssä. Se tarkoittaa, että kaksi kärkipistettä on vierekkäin ’G-’:ssä, jos kaksi kärkipistettä ei ole vierekkäin G:ssä.
Jos graafissa I olevat reunat puuttuvat toisesta graafista II, ja jos sekä graafi I että graafi II yhdistetään täydelliseksi graafiksi, niin graafia I ja graafia II sanotaan toistensa komplementeiksi.
Esimerkki
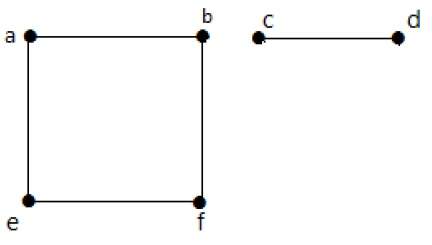
Seuraavassa esimerkissä graafissa I on kaksi reunaa ’cd’ ja ’bd’. Sen komplementtigraafissa-II on neljä reunaa.
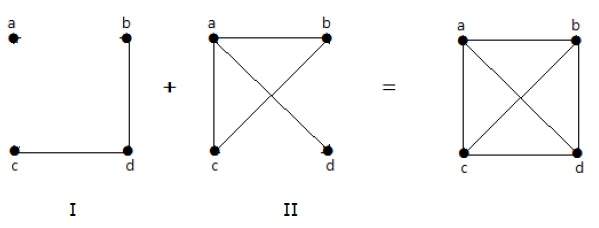
Huomaa, että graafin-I reunoja ei ole graafissa-II ja päinvastoin. Näin ollen molempien graafien yhdistelmä antaa täydellisen graafin, jossa on ’n’ kärkeä.
Huomautus – Kahden toisiaan täydentävän graafin yhdistelmä antaa täydellisen graafin.
Jos ’G’ on mikä tahansa yksinkertainen graafi, niin
|E(G)| + |E(’G-’)| = |E(Kn)|, missä n = graafin kärkien lukumäärä.
Esimerkki
Jos ’G’ on yksinkertainen graafi, jossa on yhdeksän kärkeä ja kaksitoista särmää, etsitään ’G-’:n särmien lukumäärä.
Tulokseksi saadaan, |E(G)| + |E(’G-’)| = |E(Kn)|
12 &plussat; |E(’G-’)| =
.