Hay varios tipos de grafos dependiendo del número de vértices, el número de aristas, la interconectividad y su estructura general. En este capítulo sólo hablaremos de algunos tipos importantes de grafos.
Grafo nulo
Un grafo que no tiene aristas se llama grafo nulo.
Ejemplo

En el grafo anterior, hay tres vértices llamados ‘a’, ‘b’ y ‘c’, pero no hay aristas entre ellos. Por lo tanto, es un gráfico nulo.
Gráfico trivial
Un gráfico con un solo vértice se llama gráfico trivial.
Ejemplo
En el gráfico anterior, sólo hay un vértice ‘a’ sin otras aristas. Por lo tanto, es un gráfico trivial.
Gráfico no dirigido
Un gráfico no dirigido contiene aristas pero las aristas no son dirigidas.
Ejemplo
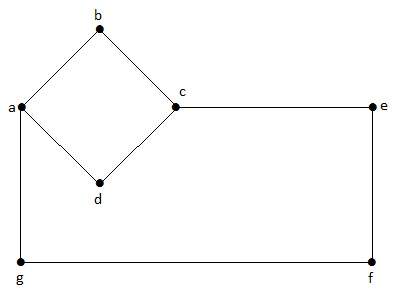
En este grafo, ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’ son los vértices, y ‘ab’, ‘bc’, ‘cd’, ‘da’, ‘ag’, ‘gf’, ‘ef’ son las aristas del grafo. Como se trata de un grafo no dirigido, las aristas ‘ab’ y ‘ba’ son las mismas. Del mismo modo, otras aristas también se consideran de la misma manera.
Gráfico dirigido
En un grafo dirigido, cada arista tiene una dirección.
Ejemplo
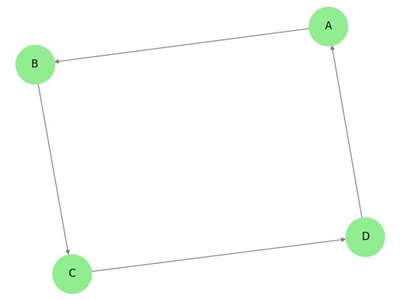
En el grafo anterior, tenemos siete vértices ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, y ‘g’, y ocho aristas ‘ab’, ‘cb’, ‘dc’, ‘ad’, ‘ec’, ‘fe’, ‘gf’, y ‘ga’. Como se trata de un grafo dirigido, cada arista lleva una flecha que indica su dirección. Obsérvese que en un grafo dirigido, ‘ab’ es diferente de ‘ba’.
Grafo simple
Un grafo sin bucles y sin aristas paralelas se llama grafo simple.
-
El número máximo de aristas posible en un grafo simple con ‘n’ vértices es nC2 donde nC2 = n(n – 1)/2.
-
El número de grafos simples posibles con ‘n’ vértices = 2nc2 = 2n(n-1)/2.
Ejemplo
En el siguiente grafo, hay 3 vértices con 3 aristas que es el máximo excluyendo las aristas paralelas y los bucles. Esto se puede demostrar utilizando las fórmulas anteriores.
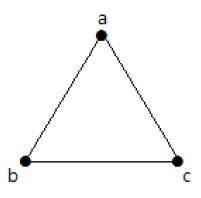
El número máximo de aristas con n=3 vértices –
nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
El número máximo de grafos simples con n=3 vértices –
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
Estos 8 grafos son los que se muestran a continuación –
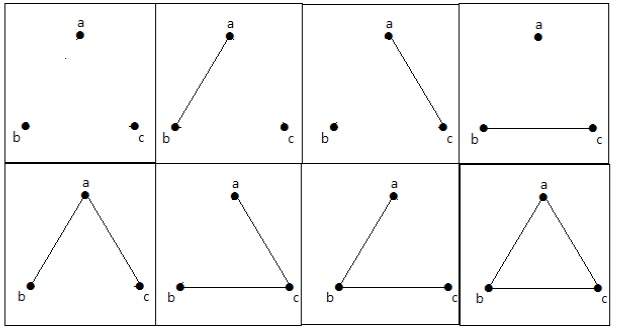
Grafo conectado
Se dice que un grafo G es conectado si existe un camino entre cada par de vértices. Debe haber al menos una arista por cada vértice del grafo. Para que podamos decir que está conectado a algún otro vértice al otro lado de la arista.
Ejemplo
En el siguiente gráfico, cada vértice tiene su propia arista conectada a otra arista. Por tanto, es un grafo conexo.
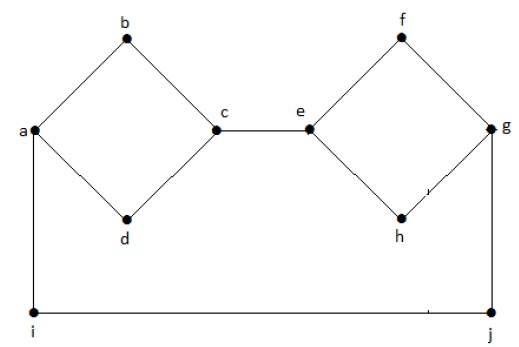
Grafo desconectado
Un grafo G es desconectado, si no contiene al menos dos vértices conectados.
Ejemplo 1
El siguiente gráfico es un ejemplo de Gráfico Desconectado, donde hay dos componentes, uno con vértices ‘a’, ‘b’, ‘c’, ‘d’ y otro con vértices ‘e’, ‘f’, ‘g’, ‘h’.
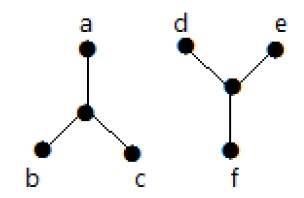
Los dos componentes son independientes y no están conectados entre sí. Por lo tanto, se llama gráfico desconectado.
Ejemplo 2
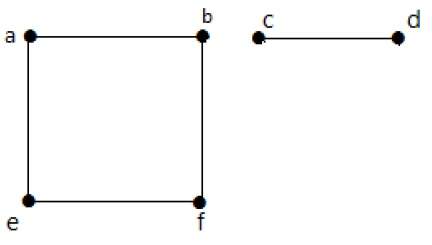
En este ejemplo, hay dos componentes independientes, a-b-f-e y c-d, que no están conectados entre sí. Por tanto, se trata de un grafo desconectado.
Grafo regular
Se dice que un grafo G es regular, si todos sus vértices tienen el mismo grado. En un grafo, si el grado de cada vértice es ‘k’, entonces el grafo se llama ‘grafo k-regular’.
Ejemplo
En los siguientes grafos, todos los vértices tienen el mismo grado. Así que estos gráficos se llaman gráficos regulares.
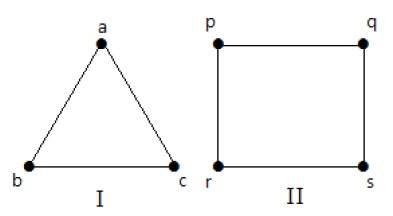
En ambos gráficos, todos los vértices tienen grado 2. Se llaman grafos 2-Regulares.
Grafo Completo
Un grafo simple con ‘n’ vértices mutuos se llama grafo completo y se denota por ‘Kn’. En el grafo, un vértice debe tener aristas con todos los demás vértices, entonces se llama grafo completo.
En otras palabras, si un vértice está conectado con todos los demás vértices de un grafo, entonces se llama grafo completo.
Ejemplo
En los siguientes grafos, cada vértice del grafo está conectado con todos los restantes vértices del grafo excepto con él mismo.
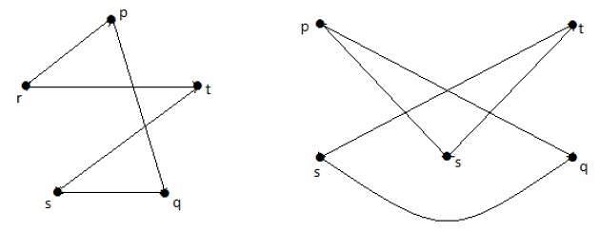
En el gráfico I,
| a | b | c | |
|---|---|---|---|
| a | No conectado | Conectado | Conectado |
| b | Conectado | No conectado | Conectado |
| c | Conectado | Conectado | No conectado |
En el gráfico II,
| p | q | r | s | |
|---|---|---|---|---|
| p | No Conectado | Conectado | Conectado | Conectado |
| q | Conectado | No conectado | Conectado | Conectado |
| r | Conectado | Conectado | No Conectado | Conectado |
| s | Conectado | Conectado | Conectado | Sin Conectado |
Gráfico de ciclos
Un gráfico simple con ‘n’ vértices (n >= 3) y ‘n’ aristas se llama gráfico de ciclos si todas sus aristas forman un ciclo de longitud ‘n’.
Si el grado de cada vértice del grafo es dos, entonces se llama grafo de ciclo.
Notación – Cn
Ejemplo
Mira los siguientes grafos –
-
El grafo I tiene 3 vértices con 3 aristas que está formando un ciclo ‘ab-bc-ca’.
-
El gráfico II tiene 4 vértices con 4 aristas que forman el ciclo ‘pq-qs-sr-rp’.
-
El gráfico III tiene 5 vértices con 5 aristas que forman el ciclo ‘ik-km-ml-lj-ji’.
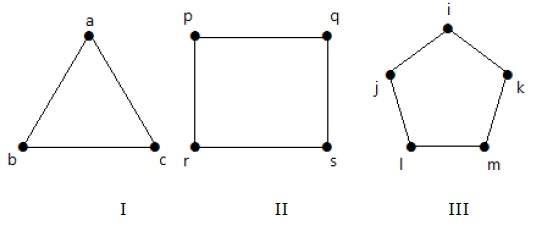
Por tanto, todos los gráficos dados son gráficos de ciclos.
Gráfico de ruedas
Un gráfico de ruedas se obtiene a partir de un gráfico de ciclos Cn-1 añadiendo un nuevo vértice. Ese nuevo vértice se llama Hub que está conectado a todos los vértices de Cn.
Notación – Wn
No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)
Ejemplo
Mira los siguientes grafos. Todos son gráficos de rueda.
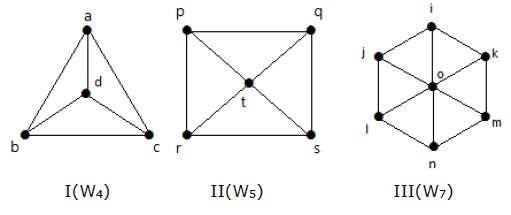
En el gráfico I, se obtiene a partir de C3 añadiendo un vértice en el centro denominado ‘d’. Se denota como W4.
Number of edges in W4 = 2(n-1) = 2(3) = 6
En el gráfico II, se obtiene a partir de C4 añadiendo un vértice en el centro llamado ‘t’. Se denota como W5.
Number of edges in W5 = 2(n-1) = 2(4) = 8
En el gráfico III, se obtiene a partir de C6 añadiendo un vértice en el centro llamado ‘o’. Se denota como W7.
Number of edges in W4 = 2(n-1) = 2(6) = 12
Gráfico cíclico
Un gráfico con al menos un ciclo se llama gráfico cíclico.
Ejemplo
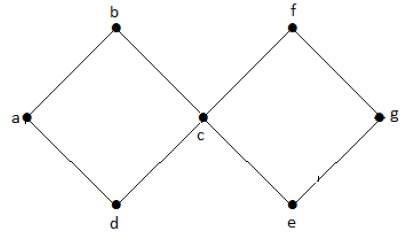
En el gráfico de ejemplo anterior, tenemos dos ciclos a-b-c-d-a y c-f-g-e-c. Por lo tanto, se llama un gráfico cíclico.
Gráfico acíclico
Un gráfico sin ciclos se llama gráfico acíclico.
Ejemplo
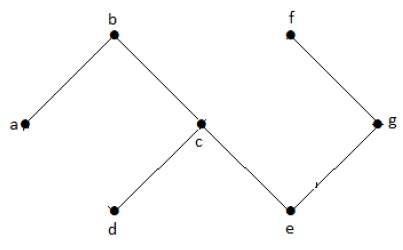
En el gráfico de ejemplo anterior, no tenemos ningún ciclo. Por lo tanto es un grafo no cíclico.
Grafo bipartito
Un grafo simple G = (V, E) con partición de vértices V = {V1, V2} se llama grafo bipartito si cada arista de E une un vértice de V1 con un vértice de V2.
En general, un grafo bipartito tiene dos conjuntos de vértices, digamos, V1 y V2, y si se dibuja una arista, ésta debe conectar cualquier vértice del conjunto V1 con cualquier vértice del conjunto V2.
Ejemplo
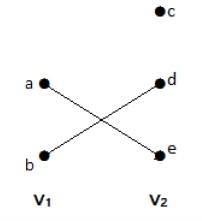
En este grafo, se observan dos conjuntos de vértices – V1 y V2. Aquí, dos aristas llamadas ‘ae’ y ‘bd’ están conectando los vértices de dos conjuntos V1 y V2.
Gráfico bipartito completo
Un gráfico bipartito ‘G’, G = (V, E) con partición V = {V1, V2} se dice que es un gráfico bipartito completo si cada vértice en V1 está conectado a cada vértice de V2.
En general, un grafo bipartito completo conecta cada vértice del conjunto V1 con cada vértice del conjunto V2.
Ejemplo
El siguiente grafo es un bipartito completo porque tiene aristas que conectan cada vértice del conjunto V1 con cada vértice del conjunto V2.
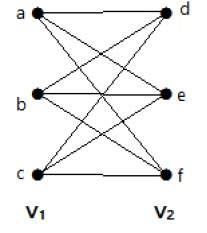
Si |V1| = m y |V2| = n, entonces el grafo bipartito completo se denota por Km, n.
-
Km,n tiene (m+n) vértices y (mn) aristas.
-
Km,n es un grafo regular si m=n.
En general, un grafo bipartito completo no es un grafo completo.
Km,n es un grafo completo si m=n=1.
El número máximo de aristas en un grafo bipartito con n vértices es
Si n=10, k5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25
De forma similar K6, 4=24
K7, 3=21
K8, 2=16
K9, 1=9
Si n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20
Similarmente K6, 3=18
K7, 2=14
K8, 1=8
‘G’ es un grafo bipartito si ‘G’ no tiene ciclos de longitud impar. Un caso especial de grafo bipartito es el grafo estrella.
Grafo estrella
Un grafo bipartito completo de la forma K1, n-1 es un grafo estrella con n vértices. Un grafo estrella es un grafo bipartito completo si un solo vértice pertenece a un conjunto y todos los vértices restantes pertenecen al otro conjunto.
Ejemplo
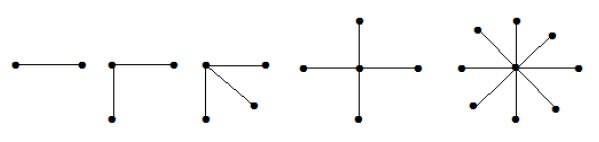
En los grafos anteriores, de ‘n’ vértices, todos los ‘n-1’ vértices están conectados a un solo vértice. Por lo tanto, es en la forma de K1, n-1 que son gráficos de estrella.
Complemento de un gráfico
Sea ‘G-‘ un gráfico simple con algunos vértices como el de ‘G’ y una arista {U, V} está presente en ‘G-‘, si la arista no está presente en G. Significa, dos vértices son adyacentes en ‘G-‘ si los dos vértices no son adyacentes en G.
Si las aristas que existen en el grafo I están ausentes en otro grafo II, y si tanto el grafo I como el grafo II se combinan juntos para formar un grafo completo, entonces el grafo I y el grafo II se llaman complementos el uno del otro.
Ejemplo
En el siguiente ejemplo, el grafo-I tiene dos aristas ‘cd’ y ‘bd’. Su complemento gráfico-II tiene cuatro aristas.
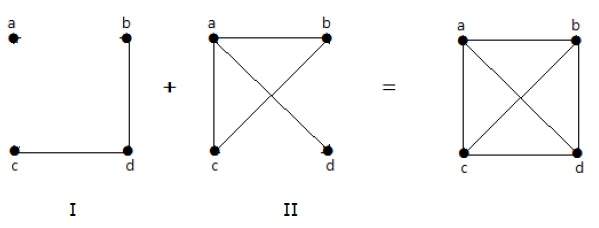
Nótese que las aristas del gráfico-I no están presentes en el gráfico-II y viceversa. Por lo tanto, la combinación de ambos gráficos da un gráfico completo de ‘n’ vértices.
Nota – Una combinación de dos gráficos complementarios da un gráfico completo.
Si ‘G’ es cualquier gráfico simple, entonces
|E(G)| + |E(‘G-‘)| = |E(Kn)|, donde n = número de vértices en el gráfico.
Ejemplo
Siendo ‘G’ un grafo simple con nueve vértices y doce aristas, encuentra el número de aristas en ‘G-‘.
Tienes, |E(G)| + |E(‘G-‘)| = |E(Kn)|
12 + |E(‘G-‘)| =