Introducción a la estadística empresarial

Considere el siguiente conjunto de datos.
4; 5; 6; 6; 6; 7; 7; 7; 7; 8; 8; 8; 9; 10

Este conjunto de datos puede representarse mediante el siguiente histograma. Cada intervalo tiene una anchura de uno, y cada valor está situado en el centro de un intervalo.

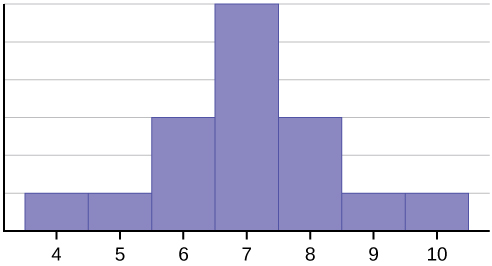
El histograma muestra una distribución simétrica de los datos. Una distribución es simétrica si se puede trazar una línea vertical en algún punto del histograma de forma que la forma a la izquierda y a la derecha de la línea vertical sean imágenes especulares entre sí. La media, la mediana y la moda son cada una siete para estos datos. En una distribución perfectamente simétrica, la media y la mediana son iguales. Este ejemplo tiene una moda (unimodal), y la moda es la misma que la media y la mediana. En una distribución simétrica que tiene dos modos (bimodal), los dos modos serían diferentes de la media y la mediana.

El histograma para los datos: 4566677778 no es simétrico. El lado derecho parece «cortado» en comparación con el lado izquierdo. Una distribución de este tipo se denomina sesgada a la izquierda porque está arrancada hacia la izquierda. Podemos medir formalmente la asimetría de una distribución del mismo modo que podemos medir matemáticamente el peso del centro de los datos o su «velocidad» general. La fórmula matemática para la asimetría es: . Cuanto mayor sea la desviación de cero, mayor será el grado de asimetría. Si la asimetría es negativa, la distribución está sesgada a la izquierda, como en la figura. Una medida positiva de la asimetría indica una asimetría hacia la derecha como en (Figura).

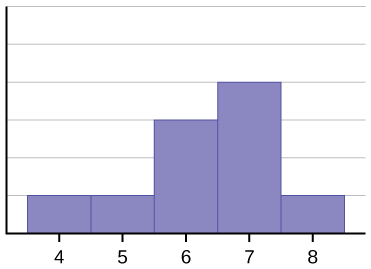
La media es 6,3, la mediana es 6,5 y la moda es siete. Observa que la media es menor que la mediana, y ambas son menores que la moda. Tanto la media como la mediana reflejan el sesgo, pero la media lo refleja más.

El histograma de los datos: 67777888910, tampoco es simétrico. Está sesgado hacia la derecha.

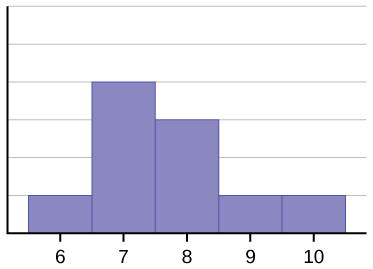
La media es 7,7, la mediana es 7,5 y la moda es siete. De las tres estadísticas, la media es la mayor, mientras que la moda es la menor. De nuevo, la media es la que más refleja el sesgo.

Para resumir, generalmente si la distribución de los datos está sesgada a la izquierda, la media es menor que la mediana, que suele ser menor que la moda. Si la distribución de los datos está sesgada hacia la derecha, la moda suele ser menor que la mediana, que a su vez es menor que la media.

Al igual que con la media, la mediana y la moda, y como veremos en breve, la varianza, existen fórmulas matemáticas que nos dan medidas precisas de estas características de la distribución de los datos. De nuevo mirando la fórmula de la asimetría vemos que se trata de una relación entre la media de los datos y las observaciones individuales al cubo.

donde es la desviación estándar muestral de los datos, , y es la media aritmética y es el tamaño de la muestra.

Formalmente la media aritmética se conoce como el primer momento de la distribución. El segundo momento que veremos es la varianza, y la asimetría es el tercer momento. La varianza mide las diferencias al cuadrado de los datos respecto a la media y la asimetría mide las diferencias al cubo de los datos respecto a la media. Mientras que la varianza nunca puede ser un número negativo, la medida de la asimetría sí puede y así es como determinamos si los datos están sesgados a la derecha o a la izquierda. La asimetría para una distribución normal es cero, y cualquier dato simétrico debería tener una asimetría cercana a cero. Los valores negativos de la asimetría indican que los datos están sesgados a la izquierda y los valores positivos de la asimetría indican que los datos están sesgados a la derecha. Por izquierda sesgada, queremos decir que la cola izquierda es larga en relación con la cola derecha. Del mismo modo, la desviación a la derecha significa que la cola de la derecha es más larga que la de la izquierda. La asimetría caracteriza el grado de asimetría de una distribución en torno a su media. Mientras que la media y la desviación típica son magnitudes dimensionales (por eso tomaremos la raíz cuadrada de la varianza ) es decir, tienen las mismas unidades que las magnitudes medidas , la asimetría se define convencionalmente de forma que sea adimensional. Es un número puro que caracteriza únicamente la forma de la distribución. Un valor positivo de asimetría significa una distribución con una cola asimétrica que se extiende hacia X más positivo y un valor negativo significa una distribución cuya cola se extiende hacia X más negativo. Una medida cero de asimetría indicará una distribución simétrica.

La asimetría y la simetría se vuelven importantes cuando discutimos las distribuciones de probabilidad en capítulos posteriores.